石蜡相变材料蓄热过程的模拟研究

doi:10.12028/j.issn.2095-4239.2019.0166

石蜡相变材料蓄热过程的模拟研究

邹勇^,, 仇汝冬, 王霞

安徽工业大学数理科学与工程学院，安徽马鞍山 243032

Simulation study on thermal storage process of paraffin phase change materials

ZOU Yong^,, QIU Rudong, WANG Xia

School of Mathematics and Physics, Anhui University of Technology, Ma’anshan 243032, Anhui, China

收稿日期: 2019-07-23 修回日期: 2019-08-10 网络出版日期: 2020-01-06

基金资助:

安徽省教育厅重点项目.  KJ2018A0051
安徽省创新计划项目.  201810360351
安徽工业大学质量工程项目.  2018jy41

Received: 2019-07-23 Revised: 2019-08-10 Online: 2020-01-06

作者简介 About authors

联系人：邹勇（1981—），男，博士，讲师，主要从事传热传质、能源转化与利用的研究，E-mail：yongzou@ahut.edu.cn。 E-mail：yongzou@ahut.edu.cn。

摘要

太阳能以其分布广、储量大以及极易获取的特点，成为人们发展清洁能源的首选对象，但太阳能的利用亦受到天气和季节的不利影响，如何高效地将太阳能储存起来仍是目前亟待解决的问题。掌握相变材料蓄热过程的影响因素对提高太阳能的利用率具有重要的指导意义。本工作建立了管壳式相变储能换热器的二维CFD模型，基于FLUENT软件的凝固/熔化模型，以石蜡为相变材料对其熔化过程进行仿真，分析了自然对流、石蜡厚度以及壁温对石蜡相变换热过程的影响。结果表明，自然对流对石蜡熔化起着显著作用；石蜡熔化总时间随石蜡厚度的增加而增加；并非壁温越高熔化速度越快，达到一定温度后，壁温对熔化过程的影响不大。

关键词： 管壳相变储能 ; 石蜡 ; 自然对流 ; 热源温度 ; 数值模拟

Abstract

Solar energy is the first choice for developing clean energy because of its wide distribution, large reserves, and easy access. However, solar energy is affected by adverse weather conditions and seasons. Efficient methods for storing solar energy remain an urgent problem. Thus, understanding the factors that influence the thermal storage process of the phase change materials (PCMs) is important to improve the solar energy utilization rate. In this study, a two-dimensional (2-d) computational fluid dynamics model is developed on a shell-and-tube phase change energy storage heat exchanger. The melting process of the PCMs (paraffin wax) is numerically simulated using a solidification and melting model in FLUENT. The effects of the natural convection, paraffin thickness, and wall temperature on the heat transfer characteristics of the heat exchanger are studied during the charging process. Natural convection is demonstrated to significantly affect the growth of the PCM interface shape. The total melting time of paraffin increases with its thickness; however, it is not clear if a higher wall temperature of the heat-carrier fluid results in a faster melting rate. The influence of the wall temperature on the melting time significantly weakens when it exceeds the threshold.

Keywords： tube shell phase change energy storage ; paraffin wax ; natural convection ; heat source temperature ; numerical simulation

PDF (1756KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

邹勇, 仇汝冬, 王霞. 石蜡相变材料蓄热过程的模拟研究. 储能科学与技术[J], 2020, 9(1): 101-108 doi:10.12028/j.issn.2095-4239.2019.0166

ZOU Yong. Simulation study on thermal storage process of paraffin phase change materials. Journal of Laparoscopic Surgery[J], 2020, 9(1): 101-108 doi:10.12028/j.issn.2095-4239.2019.0166

能源短缺和环境污染是人类社会发展道路上不得不面对的问题。由于传统能源如石油、煤炭等有不可再生和污染大的特点，已不能满足社会可持续发展的需要，必须发展清洁新能源。而太阳能无疑是首选发展对象，不仅仅因为太阳能储量最大和分布最广，还得益于其极易获取。但太阳能受到诸多因素的影响，比如天气和季节。为解决太阳能在供应和使用时间上的不匹配，就需要一种能量储存技术，在太阳能充足时储存能量，不足时释放能量^[1]。

储能技术是一种能缓解能源供需双方在时间和强度上不匹配，提高能源利用率和减轻环境污染的技术^[2,3]。相变蓄热即潜热蓄热，利用相变材料在物相变化时吸收或释放大量的热量，以与外界交换能量。目前，最常用的储能方式是固-液相变蓄热，其具有蓄热密度大、温度恒定、蓄热容器体积小、易于操作和管理的特点^[4,5]。

随着信息技术和互联网的高速发展，人们研究事物的方式也越来越多样化和便捷化。对于相变蓄热系统的研究方式，主要有实验、数值模拟、数值模拟和实验相结合3种。李新国等^[6]以石蜡作为相变材料建立了圆外管相变实验系统，得到了蓄放热时不同位置石蜡相变规律以及石蜡熔化时间。杨佳霖等^[7]以管壳式相变蓄热结构为对象，采用DSC示差扫描量热法对石蜡的热物性进行测量，获得了石蜡的相变温度及相变潜热。华维三等^[8]开展了纳米金属/石蜡复合相变蓄热材料的实验研究，以提高复合相变材料的导热性能。王慧儒等^[9]采用高清相机和红外热像技术，对组合相变材料融化-凝固循环过程的传热特性开展了可视化实验研究。

张云婷等^[10]利用焓法建立壳管式相变材料蓄热装置的数学模型，使用FLUENT的凝固/熔化模型模拟了石蜡熔化的相变过程，得到了热流体的温度对相变过程起主要作用，热流体流速的影响则相对较小的结论。Zheng等^[11]研究了内管数量和入口温度对换热器蓄热过程传热特性的影响，结果显示采用直径较小的管道和较高的进口温度均可缩短相变材料（PCM）的熔化时间。Abdulrahman等^[12]选择具有三角形内壁的相变材料石蜡在矩形换热器中的蓄热情况。结果表明，在PCM的熔化过程中，热流体的雷诺数起着积极的作用，增加热流体的雷诺数将增加传热率并导致PCM的快速熔化。刘刚等^[13]进行了翅片强化管壳式相变蓄热器传热的模拟分析，得到了不同翅片数量随时间变化的液体组分云图以及翅片管中相变材料完全融化的温度分布云图。袁培等^[14]的仿真结果显示，熔化过程中添加翅片可增强导热效果使得相变材料分布均匀，既加快了传热又能在相变材料熔化过程中维持相变材料分布的相对均匀性，提升了蓄热效率。

姜亚慧^[15]选用石蜡类相变材料作为建筑墙体的蓄热材料，利用差示扫描量热仪对混合石蜡相变材料的相变潜热、相变温度及其稳定性进行了实验研究，同时构建模型利用FLUENT对其温度场进行数值模拟，最后对比两种方式得到的结果。陈华等^[16] 仿真结果显示，将泡沫金属铜加入到装有纯石蜡的相变蓄热箱中，可以大大提高石蜡的蓄热性能，缩短了石蜡相变的时间，其与实验结论一致。

综上，对于蓄热式换热器而言，蓄热系统的性能受多种因素的影响，为了优化蓄热系统的性能，应仔细选择相变材料及换热器的设计参数。目前，国内外学者对蓄热系统展开了一系列研究，实验的方法虽然直观，但测量过程存在着困难，不利于系统分析，同时受人力、物力等条件限制，实验不可能做到面面俱到。相比之下，数值模拟的方式更为便捷，且行之有效，已被用于太阳能热利用、工业余热回收、采暖空调等节能领域的研究^[17,18,19]。本工作以石蜡为相变材料，数值研究自然对流、换热介质温度及换热器参数对蓄热性能的影响，为实际应用提供技术支持。

1 模型构建

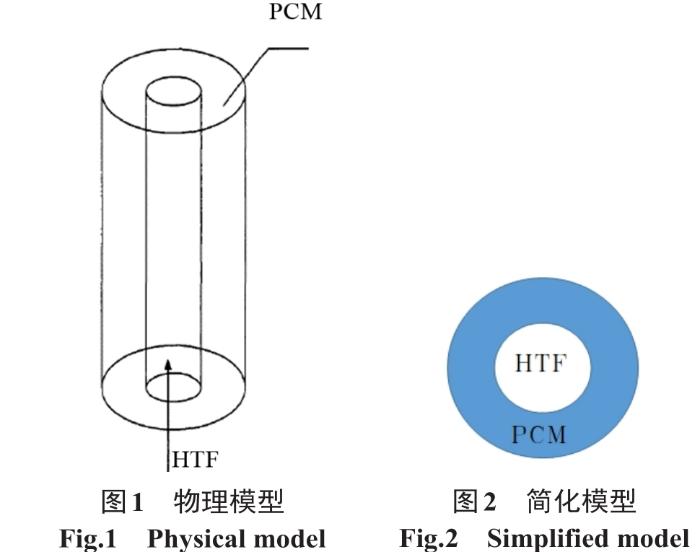
1.1　物理模型

如图1所示，本文研究了一种管壳式蓄热装置。该装置的中心是铜管，以水作为换热介质（HTF），流经铜管时与外界进行热量交换。蓄热装置外壁为铝制材料。相变材料（PCM）石蜡填充在铜管的外壁和装置的内壁之间。铜管管径为14 mm，外管管径可变，管壁厚度不计。当水从铜管中流过时，石蜡从中吸收能量，逐渐熔化，蓄热过程渐渐完成。当管长与管径之比不太大时，换热流体的入口和出口温度基本相同，管长度方向上的热量传递可以忽略，因此，只需要分析其中一个横截面的相变过程即可获得全部的蓄热情况。把蓄热问题从三维模型转化为二维模型，可以大大降低研究的难度，简化模型如图2所示。并假设：①外管壁面与外界绝热；②内管作为热源加热相变材料；③相变材料液体流动为层流；④石蜡从固体到液体的体积。变化可以忽略。

1.2　数学模型

从传热的角度来看，石蜡熔化过程中的固液相问题的本质是相变传热，也被称为Stefan问题。对于相变材料，所谓的固相和液相的分界面实际上是一个具有一定厚度的两相糊状区。石蜡熔化或凝固时，相界面处伴随着潜热吸收或释放。相变过程中，由于石蜡的密度随温度变化，在重力作用下，液相区域会发生自然对流。相变过程中最难处理的问题是如何及时追踪相界面。FLUENT软件对熔化/凝固问题的处理采用的是由Voller等^[20]和Prakash等^[21]提出的焓-孔隙率的计算方法，引入液相分数来间接的描述固-液界面的变化过程，可以处理等温相变和一定相变温度范围的相变问题。液相分数是指液相区域在整个蓄热单元中所占的比例，可以通过焓的平衡来计算，同时在动量方程中加入一个合理的源项来求解固相存在时的压降。

焓法以蓄热材料的温度和焓一起作为求解变量，这样可以在整个区域（包括液相、固相和两相界面糊状区）建立统一的能量方程，先求出焓的分布。然后，根据温度和焓的已知关系得到节点的温度值^[19]，其控制方程为

\frac{∂ ρ}{∂ t} + \frac{∂ (ρ u)}{∂ x} + \frac{∂ (ρ v)}{∂ y} = 0

(1)

ρ (\frac{∂ u}{∂ t} + u \frac{∂ u}{∂ x} + v \frac{∂ u}{∂ y}) = μ (\frac{∂^{2} u}{∂ x^{2}} + \frac{∂^{2} u}{∂ y^{2}}) - \frac{∂ p}{∂ x} + S_{u}

(2)

ρ (\frac{∂ v}{∂ t} + u \frac{∂ v}{∂ x} + v \frac{∂ v}{∂ y}) = μ (\frac{∂^{2} v}{∂ x^{2}} + \frac{∂^{2} v}{∂ y^{2}}) - \frac{∂ p}{∂ y} + S_{v}

(3)

ρ (\frac{∂ H}{∂ t} + u \frac{∂ H}{∂ x} + v \frac{∂ H}{∂ y}) = \frac{λ}{c_{p}} (\frac{∂^{2} H}{∂ x^{2}} + \frac{∂^{2} H}{∂ y^{2}}) + S_{h}

(4)

式中，u，v为速度V的x方向上和y方向上的分量；ρ为密度；μ为动力黏度；λ为导热系数；c_p为比热容；p为压强；S_u，S_v分别为x，y方向上的动量源项；S_h为能量源项。

关于焓的方程

H = h + Δ H

(5)

h = h_{r e f} + \int_{T_{r e f}}^{T} c_{p} d T

(6)

Δ H = β L

(7)

β = \{\begin{matrix} 0 & T < T_{s} \\ \frac{T - T_{s}}{T_{l} - T_{s}} & T_{s} < T < T_{l} \\ 1 & T > T_{l} \end{matrix}

(8)

式中，h为显热；L为相变潜热；T_ref为参考温度；h_ref为参考温度下相变材料所对应的焓；β为液相分数；T_l是指材料的液相温度；T_s是指材料的固相温度。

动量方程和能量方程源项分别为

S_{u} = \frac{{(1 - β)}^{2}}{β^{3} + ε} A_{m u s h} u

(9)

S_{v} = \frac{{(1 - β)}^{2}}{β^{3} + ε} A_{m u s h} v - ρ_{r e f} g [1 - α (T - T_{r e f})]

(10)

S_{h} = \frac{ρ ∂ (Δ H)}{c_{p} ∂ t}

(11)

式中，ε为小于0.001的常数，避免分母为0；A_mush为糊状区常数，通常取10⁵；ρ_ref为参考温度时密度；g为重力加速度；α为体膨胀系数。

2 相变过程模拟

为了保证模拟结果的正确性，首先进行网格独立性验证。将外管半径为35 mm的二维简化模型进行网格划分，划分网格数分别为4140、5200、6160和7440，设置两个监测点，坐标分别为point 1（15 mm,0）和point 2（0,15 mm），当蓄热时间相同时，得到的验证结果如表1所示。所选的四种网格下监测点的温度最大偏差为0.8%，此时两监测点均处于相变界面处（即两相糊状区），与预期相符，同时结合石蜡相变界面的清晰度，最终选择网格数为6160的蓄热单元进行模拟，网格划分图如图3所示。其他尺寸的二维模型网格独立性验证过程类似，在此不再赘述。一般只有在一个时间步长内迭代次数能够达到指定的残差，这个时间步长才是合适的，否则就要减少时间步长。经过多次测试，选择了时间步长为0.1 s。

表1 不同网格数下监测点的温度

Table 1 Temperature of monitoring points under different grid numbers

网格数	4140	5200	6160	7440
Point 1处温度	327.68723	327.74619	327.63763	327.70667
Point 2处温度	327.53781	327.64267	327.53831	327.41254

新窗口打开| 下载CSV

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 网格划分

Fig.3 Mesh division

启用基于压力的Navier-Stokes解算算法，选择2D分离式，以非稳态模式进行求解；激活FLUENT软件的Solidification/Melting 模块对石蜡熔化过程进行计算；设置相变材料的物性参数，见表2；设置操作环境，如果考虑自然对流因素，将重力选项勾选上，方向为y负方向，其他的保持默认值；设置边界条件，蓄热单元内壁面温度根据研究需要设置不同的数值，外壁面绝热；差分格式和松弛因子均采用默认值；初始温度设为293 K。

表2 相变材料物性参数^[22]

Table 2 Physical properties of phase change material

参数	数值
固相比热容/J·(kg·K)^-1	2464
液相比热容/J·(kg·K)^-1	2950
固相密度/kg·m^-3	900
液相密度/kg·m^-3	773
膨胀系数/1·K^-1	0.001
动力粘度/kg·m·s^-1	0.03
固相导热系数/W·(m·K)^-1	0.28
液相导热系数/W·(m·K)^-1	0.14
凝固温度/K	325
熔化温度/K	328
熔化潜热/J·kg^-1	205600

新窗口打开| 下载CSV

考虑自然对流的影响时，需将密度项选择Boussinesq假设，值为900 kg/m³。对于大多数自然对流，只要实际密度变化很小，就可以认为该假设是精确的近似。若不考虑自然对流，密度值为常数900 kg/m³。并且石蜡液相、固相的物理性质有所变化，为了计算结果的准确性，将石蜡的比热容、导热系数分段设置。纯液相和纯固相区域物性参数分别为常数，在两相糊状区对其进行线性处理，计算公式如下

c_{p} = \{\begin{matrix} 2464 & T < T_{s} \\ a T + b & T_{s} < T < T_{l} \\ 2950 & T > T_{l} \end{matrix}

(12)

λ = \{\begin{matrix} 0.28 & T < T_{s} \\ c T + d & T_{s} < T < T_{l} \\ 0.14 & T > T_{l} \end{matrix}

(13)

式中，a、b、c、d为常数。

3 模拟结果与分析

3.1　自然对流对石蜡熔化过程的影响

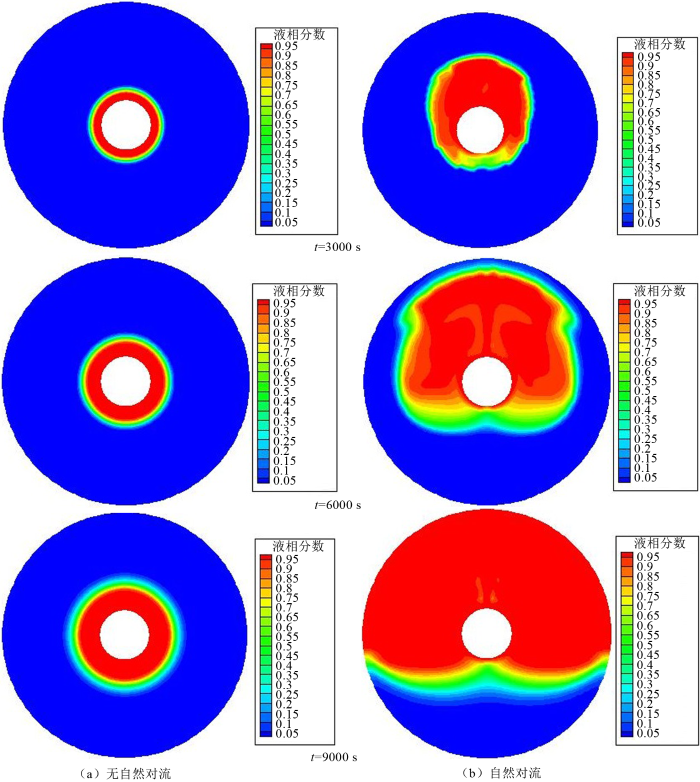
选择管径为70 mm，内壁温度为343 K的蓄热单元为研究对象，图4给出了有无对流情况下石蜡液相分数随时间的变化情况。图中红色区域是液相区，蓝色区域是固相区，介于两者之间的黄绿色区域为糊状区。对比相同时刻的两幅图，可以得出在自然对流作用下，石蜡熔化得更快。在不考虑自然对流的情况下，随着时间的增长，石蜡的相变面以规则的同心圆向外壁面缓慢扩展；而在自然对流作用下，相变面向外扩展是不规则的，但左右对称，而且石蜡正上方区域先熔化再向两侧扩展，液相区域呈碗状分布，直到上半区域完全熔化，下半区域才开始熔化。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 有无自然对流条件下液相体积分数分布图

Fig.4 Liquid fraction contours under condition of natural convection or not at different time

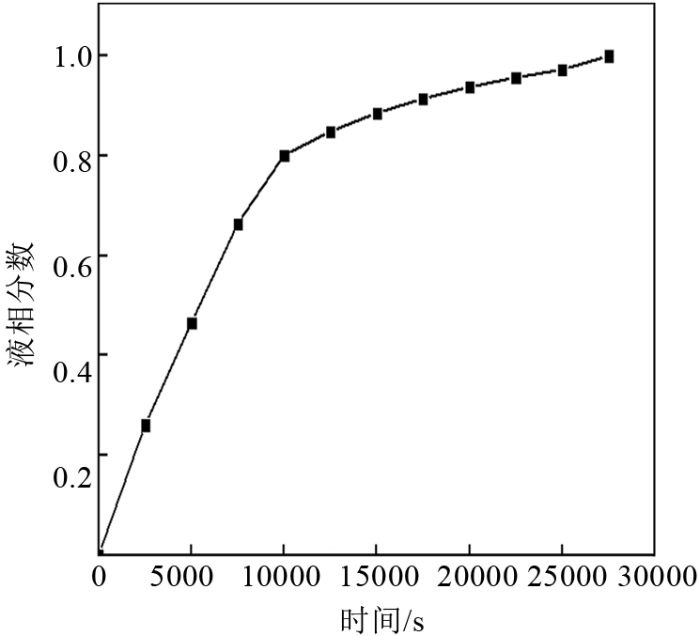
图5显示的是在自然对流作用下石蜡液相分数随时间的变化曲线图。从图中可以看出：大约前10000 s，液相分数增长非常快，这段时间里，主要是自然对流加快了石蜡的熔化进程，熔化率为80%，结合相变面变化规律来分析，可以知道此时上半部分已经完全熔化；总的熔化时间为27500 s，最后20%的石蜡熔化时间占总时长的60%，由于在下半区未熔化的石蜡未受到浮力作用，而且未被熔化的区域离加热源越来越远，热阻越来越大，因此熔化所需时间相对较长。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 液相分数变化曲线图

Fig.5 Variation curve of liquid fraction

3.2　不同厚度对石蜡熔化过程的影响

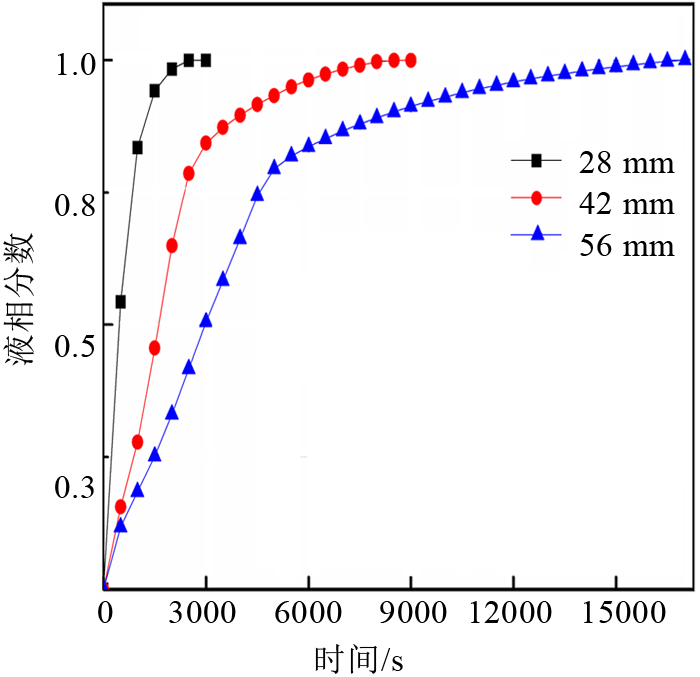
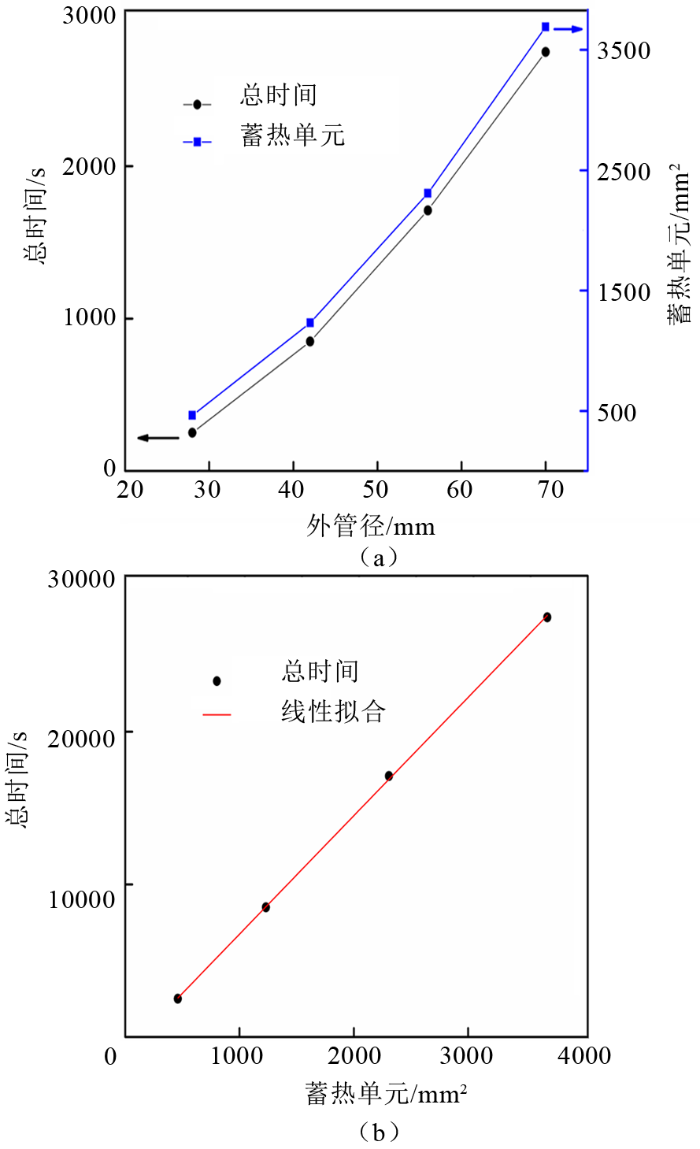
改变蓄热单元外管管径大小，分别为28 mm、42 mm、56 mm，其他条件不变，然后进行数值模拟，图6给出了不同厚度的石蜡熔化情况。从图6可以看出：当改变管径时，不同厚度的石蜡熔化的趋势是一样的，在蓄热初期，石蜡的液相分数均随时间呈线性规律迅速增长，后期熔化速度变缓。相同时刻下，石蜡的液相分数与厚度是负相关关系，也就是石蜡厚度越大，熔化的速度就越慢。计算结果显示，管径为28 mm、42 mm和56 mm的石蜡完全熔化所需时间分别为2500 s、8500 s和17100 s。图7（a）给出了石蜡完全熔化所需时间随管径的变化曲线，发现其与蓄热单元的面积随管径的变化曲线形状相似，说明熔化时间随管径的增大而呈抛物线形式增长。为证实这一结论，将石蜡完全熔化所需时间随蓄热单元的面积的变化进行线性拟合，得到其斜率为7.75，截距为-1009.64，拟合结果如图7（b）所示。根据此线性关系，可以预测其他管径下石蜡完全熔化所需要的时间。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 不同厚度石蜡液相分数变化曲线

Fig.6 Liquid fraction curves of paraffin with different thickness

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 不同厚度石蜡液相熔化总时间

Fig.7 Melting total time of paraffin with different thickness

3.3　不同壁温下石蜡的熔化过程

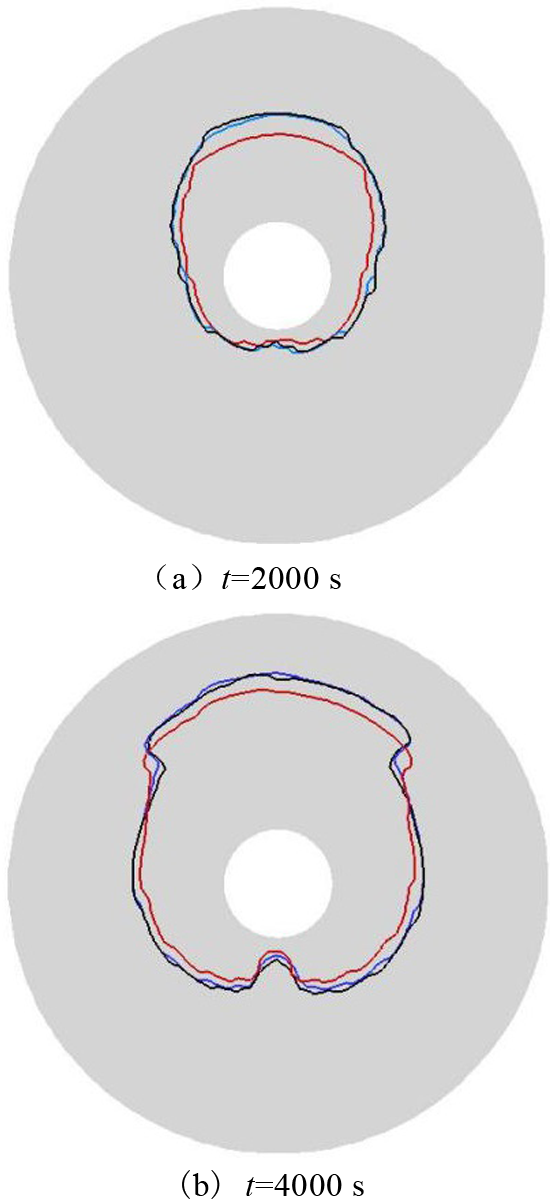
以外管半径为35 mm的蓄热装置作为研究对象，改变其内壁面温度，研究不同温度下石蜡熔化情况。图8为蓄热装置在不同时刻、不同壁温下石蜡相变面。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 不同壁温下石蜡相变面图(r=35 mm)

Fig.8 Paraffin phase change interface shapes (r=35 mm) under different wall temperatures

图8中的红色、蓝色、黑色线分别是内壁温度为340 K、350 K、360 K时的石蜡相变面形状。从图中可以得出：随着时间的增加，相变面曲线围成的面积变大；相同时刻下红色线围成的面积要比蓝色和黑色线围成的面积小，而蓝色线与黑色线几乎重合。为探究这一现象，选择管半径为28 mm的蓄热单元进一步定量分析。

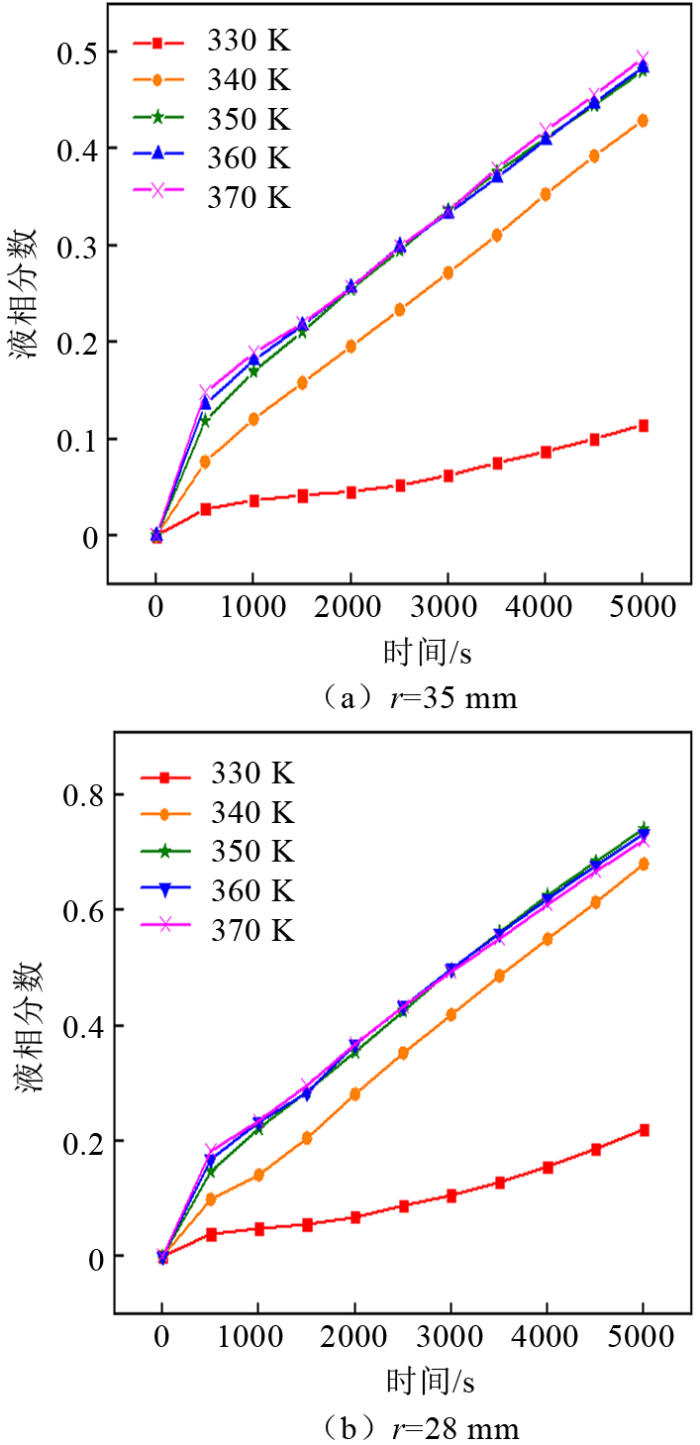
图9 给出了外管半径r分别为28 mm和35 mm的蓄热单元在不同壁温下液相分数随时间的变化曲线。由图9 （a）可以得出：在同一时刻下，外管半径为35 mm的装置当壁温从330 K升高至350 K时，石蜡的液相分数明显增大，继续增加壁温至370 K时，石蜡的液相分数变化不大，这与图8反映出的信息基本一致；如图9（b）显示，外管半径为28 mm的蓄热装置的液相分数随壁温变化规律与图9 （a）类似。由此可知，在一定范围内，提高壁温能加快石蜡熔化的速度，而当温度达到一定值时，再增加温度对石蜡熔化进程加速作用很小。壁温对熔化进程的影响存在一个临界值，这一现象与文献[11]得到的结论是一致的。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同壁温下液相分数随时间变化曲线

Fig.9 Variation curves of liquid fraction with time under different wall temperatures

4 结论

利用FLUENT软件对石蜡熔化过程进行了数值模拟，研究了自然对流对石蜡熔化的影响，并对不同厚度和不同壁温下的相变过程进行了讨论，通过分析不同时刻的液相体积分数，得到了以下结论。

（1）自然对流对石蜡熔化过程起着至关重要的作用，加速了石蜡熔化的进程，且上半区域的石蜡先熔化。

（2）对外管管径为70 mm，内壁温度为343 K的蓄热单元，石蜡总的熔化时间大约是27500 s，随着热阻越来越大，下半区熔化速度越来越慢，液相分数增长缓慢。

（3）石蜡熔化总时间与石蜡的厚度正相关，厚度越大，熔化所需时间越长。熔化总时间随厚度呈抛物线形式增长。

（4）提高壁温可以加快石蜡熔化的速度，但并非壁温越高熔化速度越快，达到一定温度后，再提高壁温对熔化过程所起的作用不大。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

VERDIER

, FALCOZ

, FERRIÈRE

Design of a protection thermal energy storage using phase change material coupled to a solar receiver

[J]. High Temperature Materials & Processes, 2014, 33(6): 509-523.