随着新能源产业的发展,锂离子电池的使用需求日益增长。与一些传统的如铅酸、镍镉等电池相比,锂电池具有能量高、自放电率低、快速充放电、无毒、无记忆效应、循环寿命长等优点。锂电池在新能源汽车、航空和配电储能系统等电源应用场景中发挥着重要作用。尽管锂电池具有很多优点,但它们也受到诸如电池材料和当前制造工艺的因素的限制,导致单体锂电池之间存在内阻、容量、电压等差异[1 ,2 ] 。在实际应用中,电池组内的单个电池容易散热不均匀或过度充电和放电。随着时间的推移,这些处于恶劣工作条件下的电池可能会提前损坏,并且电池组的整体寿命大大缩短。锂电池的安全使用仍然是一个问题,直接影响其容量和寿命的利用效率。为了确保动力电池安全可靠的运行,准确估计锂电池荷电状态(state of charge,SOC)对于能量和安全管理至关重要。目前荷电状态估算方法有安时积分、神经网络、粒子滤波、卡尔曼滤波及其改进算法等[3 ,4 ,5 ,6 ,7 ] 。温度对于锂电池具有极大影响,中国大部分地区一年温差超过30 ℃,在实际使用中,动力锂电池必须考虑温度的影响。
通过在不同温度下对电池进行容量及混合脉冲功率性能测试实验(hybridge pulse power characteristic,HPPC)获取电池特性,分析不同荷电状态、不同温度下对锂电池开路电压、欧姆内阻、极化电阻和极化电容等参数的影响,准确建立适应温度变化的Thévenin等效电路模型。由于所有算法程序运行在计算机上,可能由于计算机字长有限,存在计算误差,误差累积严重时,能使误差方差阵P k
1 理论分析
1.1 模型构建
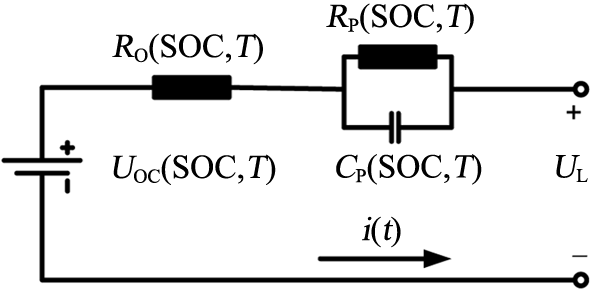
如今锂电池等效模型主要有纯数学模型、电化学模型和等效电路模型。因等效电路模型具有计算简单、物理意义明确的优点,其应用最为广泛。简单的模型易于计算,无法准确描述电池的工作特性;复杂的模型可以更好地表征电池的充放电特性,但计算量大大增加。锂电池Thévenin等效电路模型如图1 所示。
图1
图1
Thévenin 模型
Fig.1
Thévenin model
图中,U oc 表示锂电池组的开路电压;R O 表示欧姆内阻,表示电池的欧姆效应;R P 表示锂电池的极化电阻;C P 表示极化电容;RC并联电路表征电池的极化效应;i (t )表示负载电流,其中充电方向为正;U L 表示电池组外部连接时的闭路电压;T 为电池温度。根据图1 所示的电路并依据基尔霍夫定律列出电路方程如式(1)所示。
U L = U O C ( S O C ) - i ( t ) R O - U P d U P d t = - U P R P C P + i C P (1)
式中,U P 为极化电容C P 端电压。根据所采用的Thévenin等效电路模型,选取[SOC U P ]T 作为状态变量,结合式(1)及SOC的定义经过离散化可以列出锂电池状态空间方程如式(2)所示。
S O C k U P , k = 1 0 0 e x p - Δ t τ S O C k - 1 U P , k - 1 + - η Δ t Q n R P 1 1 - e x p - Δ t τ I k + w U L , k = ∂ U O C ∂ S O C - 1 S O C k U P , k - I k R O + v (2)
式中,Q n 为电池额定电量;η 为库仑效率;Δt 为采样周期;τ =R P C P 为时间常数;w 为过程噪声;v 为观测噪声。卡尔曼滤波算法将w 、v 视为高斯白噪声。
1.2 HPPC实验及参数辨识
锂电池Thévenin模型所需辨识的参数有欧姆内阻R O 、开路电压U OC 、极化电阻R P 和极化电容C P 。这里参考《美国Freedom CAR电池实验手册》对锂电池进行混合脉冲功率性能测试实验(hybridge pulse power characteristic,HPPC),以电流为激励,以端电压为响应,根据锂电池外部端电压变化,根据最小二乘原理进行离线参数辨识。研究对象为中航锂电三元锂电池LFP 50 A· h,其基本信息如表1 所示,所使用电池测试设备为亚科源BTS750-200-100-4,恒温箱为贝尔试验设备有限公司BTT-331C。
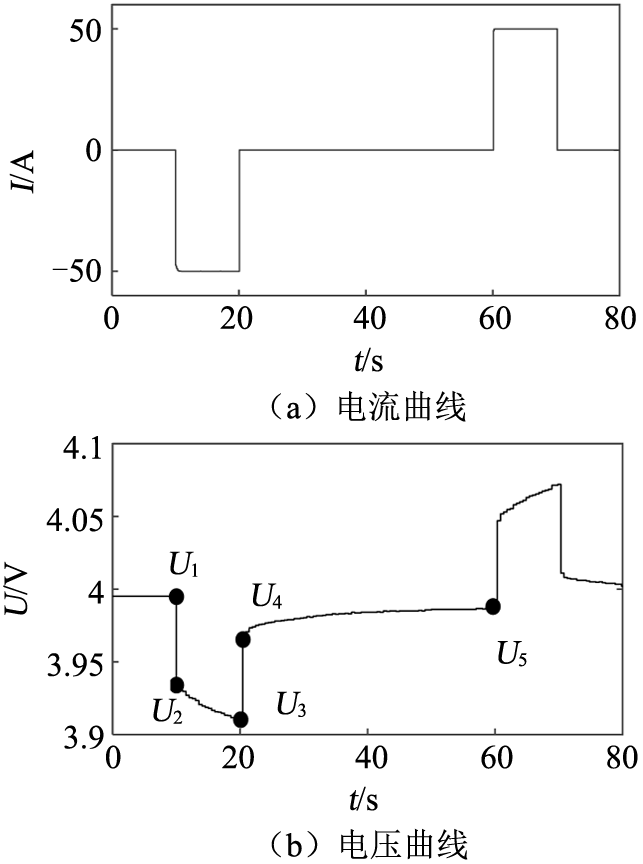
单次HPPC实验工步为:以放电倍率1 C恒流放电10 s、搁置40 s、以1 C(这里电流为50 A)恒流充电10 s、再搁置。HPPC实验中的电流曲线及其相应的电压变化曲线如图2 所示。
图2
图2
HPPC 实验电流电压曲线
Fig.2
current and voltage curves in HPPC test
通过分析图2 所示的HPPC实验电压变化曲线,可以提取变化特征以获得模型参数。图2 的分析可以提取以下特征。
(1)锂电池端电压从U 1 突降变为U 2 ,主要是由于锂电池的欧姆内阻引起的电压变化。同理,锂电池端电压从U 3 突升变为U 4 ,也是由锂电池的欧姆内阻引起的电压变化引起的。因此获取欧姆电阻R O 的值如式(3)所示。
R O = U 1 - U 2 + U 4 - U 3 2 I (3)
(2)锂电池端电压从U 2 缓慢下降到U 3 ,是由于电池极化效应造成的。放电电流对极化电容器充电,是RC回路的零状态响应。选择从U 2 到U 3 电压数据,U 2 为时间零时刻,对电路进行分析,列出方程如式(4)所示。
U L t = U 2 - I R P 1 - e - t / τ (4)
将极化电阻R O 和τ 作为未知数,根据公式(4)和t 实验数据,使用MATLAB中的曲线拟合工具,可以直接得到极化电阻R P 和时间常数τ 的值,根据τ =R P C P 计算得到极化电容C P 。
(3)开路电压U OC 是当电池长时间放置时电池在正极和负极两端稳定的电压。实验表明,电池放电40 min后的电压是稳定的,可以认为是等于电池的开路电压。因此,控制好温度、SOC值,图2 (a)中的U 1 可以作为相应的相应开路电压。
1.3 改进EKF算法
卡尔曼滤波是一种线性无偏递推滤波器,计算过程中是不断进行预测-修正。每当观测到新的数据,随时算出新的预测值,非常便于实时处理。锂电池由于放电倍率、温度和内部复杂的化学反应,呈现出非线性状态,在卡尔曼的基础上运用泰勒公式取其一阶项,省略高阶项,进行线性化处理,得到扩展卡尔曼滤波算法。锂电池模型可以用如式(5)所示状态空间方程表示。
X k = A X k - 1 + B I L , k - 1 + w U L , k = C X k + D I L , k - 1 + v (5)
式中,X k k 时刻的状态向量,X k -1 为上一时刻的状态向量,A B C D
P k | k - 1 = A P k - 1 A T K k = P k | k - 1 C T C P k | k - 1 C T + R v X k = A X k - 1 + B I L , k - 1 + K k U L , k - C X k - 1 - D I L , k - 1 P k = P k | k - 1 - K k P k | k - 1 (6)
式中,X k k 时刻根据模型及上一时刻值X k -1 直接计算出来的状态向量值,P k Kk 为Kalman增益,Rv k 时刻最优预测估计值X k P k P k P k =S k S k T ,不计算协方差矩阵改为对协方差分解矩阵S k
S k | k - 1 = A S k - 1 K k = S k | k - 1 F k α k α k = F k T F k + R v - F k = S k | k - 1 T H k γ k = 1 ± α k R 1 - α k R X k = A X k - 1 + B I L , k - 1 + K k U L , k - C X k - 1 - D I L , k - 1 S k = S k | k - 1 I - α k γ k F k F k T (7)
式中,S k|k-1 k 时刻根据模型及上一时刻值S k-1 D F k αk 、γk 为便于公式简洁的中间变量。在给定初值后,通过公式(7)进行迭代更新计算,由于将协方差矩阵P k P k
2 实验结果分析
2.1 模型参数辨识结果分析
2.1.1 参数辨识结果
通过在不同温度、不同SOC值时进行上述HPPC实验,并基于实验数据进行参数辨识,将辨识得到的Thévenin模型参数原始数据值为纵坐标,所对应的SOC为横坐标连点成线如图3 所示。
图3
图3
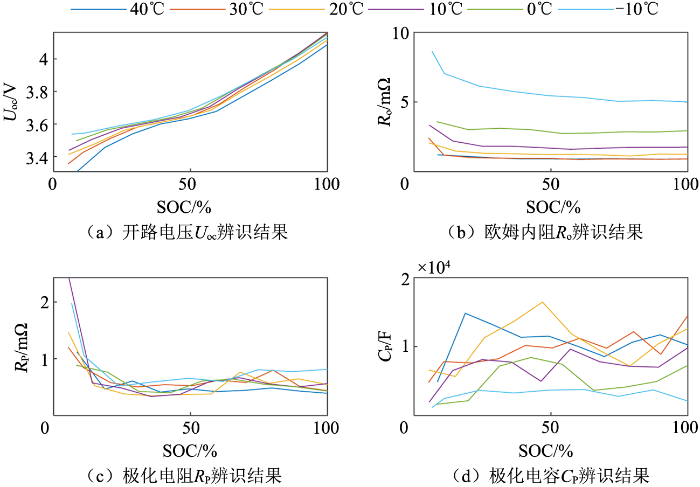
不同温度下的Thévenin 模型参数变化曲线
Fig.3
Thévenin model parameter variation curve at different temperatures
图3 (a)为不同温度下的U OC - SOC曲线,从图中可以看出,不同温度下的U OC 变化趋势一致。在SOC>20%时,不同温度下开路电压差距不大;在SOC<20%时,差异变大,温度较低时,其开路电压较高。
图3 (b)为不同温度下的R O - SOC曲线,从图中可以看出,在SOC>20%时,各温度下,欧姆内阻值相对平缓,无明显变化,可以取均值,视为欧姆内阻不变;在SOC<20%时,欧姆内阻值迅速变大。同时,40 ℃和30 ℃曲线基本重合,可以认为其欧姆内阻相同,随着温度降低,欧姆内阻增大,且每下降10 ℃,欧姆内阻加速增大。
图3 (c)为不同温度下的R p - SOC曲线,从图中可以看出,不同温度下的极化电阻R p 变化趋势一致。在SOC>20%时,极化电阻R p 无明显变化;在SOC<20%时,极化电阻R p 变大,且不同温度下的极化电阻R p 无明显区分,表明温度变化对极化电阻R p 影响相对较小。
图3 (d)为不同温度下的C p - SOC曲线,从图中可以看出,不同温度下的极化电容C p 变化相对较乱。但可以看出在SOC<20%时,不同温度下极化电容C p 都变小。随着温度的降低,极化电容C p 有较小程度的减小。
2.1.2 模型参数处理
由上述分析可知在温度不变且SOC>20%时,欧姆内阻无明显变化,故取均值。考虑温度的影响,以20 ℃下欧姆内阻值1.2391 mΩ为基准1,其他温度下的欧姆内阻值除以1.2391,得到温度影响系数ξ ,具体值如表2 所示。
选取表2 中数据根据最小二乘原理以多项式拟合的方式建立温度影响系数ξ 和温度T 的函数。这里选取三阶多项式拟合得到函数关系如式(8)所示。
ξ = 2.427 - 0.1424 T + 0.004379 T 2 - 0.000047 T 3 (8)
当SOC<20%时,在温度一定时,考虑计算复杂程度,将20 ℃时的SOC与R O 的关系用一阶线性函数表示,然后再在此之上叠加温度影响系数,最终得到R O 与SOC、T 的函数关系如式(9)所示。
R O = 1.2391 ξ S O C > 20 % ξ ( 2.813 - 7.467 × S O C ) S O C ≤ 20 % (9)
由图3 分析知温度对极化内阻、极化电容、开路电压影响较小,故选择20 ℃下所辨识的开路电压、极化内阻、极化电容值,根据最小二乘原理通过多项式拟合的方式得到函数关系如式(10)所示。
U O C = 3.352 + 1.149 × S O C - 1.617 × S O C 2 - 0.163 × S O C 3 + 3.537 × S O C 4 - 2.145 × S O C 5 R P = 0.6 S O C > 20 % 1.766 - 5.621 × S O C S O C ≤ 20 % C P = 10446 S O C > 20 % 5230 + 25150 × S O C S O C ≤ 20 % (10)
2.2 SOC估算验证
通过在不同温度、不同SOC值时进行上述HPPC实验,并基于实验数据进行参数辨识,将辨识得到的Thévenin模型参数值为纵坐标,以SOC为横坐标连点成线如图3 所示。根据2.1节所辨识出的Thévenin模型参数,选择在MATLAB上进行仿真验证在该模型下的SOC估算效果,具体模型如图4 所示。
图4
图4
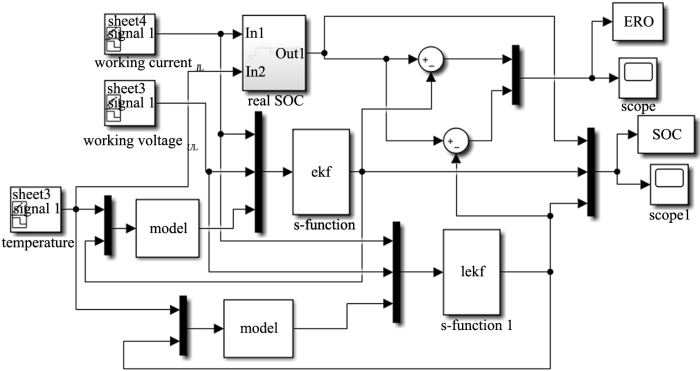
基于simulink 的SOC 估算仿真验证图
Fig.4
Simulation verification diagram of SOC estimation based on MATLAB/simulink
图4 所示仿真中,导入实验采集的真实电池电流电压温度数据到模块中作为输入,主要有三个模块,分为是根据温度和电流计算实际SOC,根据输入温度和SOC值的model函数模块,根据输入电流、电压、模型参数的EKF算法模块。这里采用的工况数据为参考北京公交动态测试(Beijing bus dynamic stress test,BBDST)工况度电池进行实验,将实验数据进行SOC估算验证。当天电池温差达到10 ℃,最低温度16 ℃,最高温度26 ℃。设定其SOC初值为90%,实际为充满电,即SOC为100%。仿真结果如图5 所示。
图5
图5
SOC 估算结果
Fig.5
SOC estimation curve
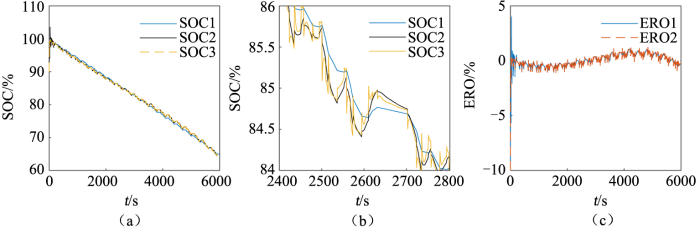
在图5 (a)中,SOC1是真实SOC值,SOC2是使用EKF算法的SOC估计值,SOC3是使用改进EKF算法的SOC估计值。图5 (b)为SOC估算结果的局部放大,这里选取84%~86%。图5 (c)是估算SOC值与实测SOC相减所得的误差曲线,ERO1是改进EKF算法估算误差,ERO2是EKF算法估算误差。
从图中可以看出,在初始误差达到10%时,算法能迅速修正初始SOC误差。迭代50s后,基于所使用变温度下的Thévenin等效电路模型运用改进EKF进行SOC估算的最大误差小于1.5%,将误差取绝对值,获得平均误差为0.37%。
3 结论
(1)温度对三元动力锂电池的欧姆内阻影响极大。在-10~40 ℃间,随着温度升高,电池欧姆内阻减小,当温度上升到30 ℃以后,欧姆内阻无明显变化。相比之下,温度对开路电压、极化电阻、极化电容影响较小。
(2)在温度一定,SOC高于20%时,三元锂电池极化电阻、极化电容、欧姆内阻值相对稳定,在SOC低于20%时,欧姆内阻、极化电阻明显增大,极化电容略微减小。
(3)改进EKF算法用于动力锂电池SOC估算,可以修正锂电池初始SOC值误差,并使最大估算误差低于1.5%,平均误差为0.37%。
(4)改进EKF算法与EKF算法比较,在粗估阶段,有较大波动,在精估阶段,改进EKF曲线相对平稳,估算更平稳。
参考文献
View Option
[1]
梁奇 , 于春梅 , 王顺利 , 等 基于PNGV电路模型的航空钴酸锂电池内阻研究
[J]. 电源学报 , 2017 , 15 (2 ): 153 -158 .
[本文引用: 1]
LIANG Qi YU Chunmei WANG Shunli et al Research on internal resistance of aviation battery based on PNGV circuit model
[J]. Journal of Power Supply , 2017 , 15 (2 ): 153 -158 .
[本文引用: 1]
[2]
WANG Shunli FERNANDEZ C ZOU Chuanyun Open circuit voltage and state of charge relationship functional optimization for the working state monitoring of the aerial lithium-ion battery pack
[J]. Journal of Cleaner Production , 2018 . 198 : 1090 -1104 .
[本文引用: 1]
[3]
蒋超宇 , 王伟超 , 杨学平 混合动力汽车磷酸铁锂动力电池建模与SOC计算
[J]. 储能科学与技术 , 2018 , 7 (5 ): 897 -901 .
[本文引用: 1]
JIANG Chaoyu WANG Weichao YANG Xueping Modeling and SOC calculations of hybrid electrical vehicles (HEV) powered by lithium iron phosphate
[J]. Energy Storage Science and Technology , 2018 , 7 (5 ): 897 -901 .
[本文引用: 1]
[4]
李争 , 张丽平 基于无迹卡尔曼滤波的锂离子电池SOC估计
[J]. 电池 , 2018 , 48 (5 ): 313 -317 .
[本文引用: 1]
LI Zheng ZHANG Liping SOC estimation of Li-ion battery based on unscented Kalman filter
[J]. Battery Bimonthly , 2018 , 48 (5 ): 313 -317 .
[本文引用: 1]
[5]
凡旭国 , 周金治 基于PNGV模型和高斯-厄米特滤波的SOC估算研究
[J]. 自动化仪表 , 2017 , 38 (12 ): 21 -26 .
[本文引用: 1]
FAN Xuguo ZHOU Jinzhi Research on SOC estimation based on PNGV Model and Gauss-Hermite filter
[J]. Process Automation Instrumentation , 2017 , 38 (12 ): 21 -26 .
[本文引用: 1]
[6]
HE Jiangtao FENG Daiwei HU Chuan Two-layer online state-of-charge estimation of lithium-ion battery with current sensor bias correction
[J]. International Journal of Energy Research , 2019 , 43 (8 ): 3837 -3852 .
[本文引用: 1]
[7]
ZENG Zhibing TIAN Jindong LI Dong An online state of charge estimation algorithm for lithium-ion batteries using an improved adaptive cubature Kalman filter
[J]. Energies , 2018 , 11 (1 ): 59 .
[本文引用: 1]
[8]
LAI Xin ZHENG Yuejiu SUN Tao A comparative study of different equivalent circuit models for estimating state-of-charge of lithium-ion batteries
[J]. Electrochimica Acta , 2018 , 259 : 566 -577 .
基于PNGV电路模型的航空钴酸锂电池内阻研究
1
2017
... 随着新能源产业的发展,锂离子电池的使用需求日益增长.与一些传统的如铅酸、镍镉等电池相比,锂电池具有能量高、自放电率低、快速充放电、无毒、无记忆效应、循环寿命长等优点.锂电池在新能源汽车、航空和配电储能系统等电源应用场景中发挥着重要作用.尽管锂电池具有很多优点,但它们也受到诸如电池材料和当前制造工艺的因素的限制,导致单体锂电池之间存在内阻、容量、电压等差异[1 ,2 ] .在实际应用中,电池组内的单个电池容易散热不均匀或过度充电和放电.随着时间的推移,这些处于恶劣工作条件下的电池可能会提前损坏,并且电池组的整体寿命大大缩短.锂电池的安全使用仍然是一个问题,直接影响其容量和寿命的利用效率.为了确保动力电池安全可靠的运行,准确估计锂电池荷电状态(state of charge,SOC)对于能量和安全管理至关重要.目前荷电状态估算方法有安时积分、神经网络、粒子滤波、卡尔曼滤波及其改进算法等[3 ,4 ,5 ,6 ,7 ] .温度对于锂电池具有极大影响,中国大部分地区一年温差超过30 ℃,在实际使用中,动力锂电池必须考虑温度的影响. ...
基于PNGV电路模型的航空钴酸锂电池内阻研究
1
2017
... 随着新能源产业的发展,锂离子电池的使用需求日益增长.与一些传统的如铅酸、镍镉等电池相比,锂电池具有能量高、自放电率低、快速充放电、无毒、无记忆效应、循环寿命长等优点.锂电池在新能源汽车、航空和配电储能系统等电源应用场景中发挥着重要作用.尽管锂电池具有很多优点,但它们也受到诸如电池材料和当前制造工艺的因素的限制,导致单体锂电池之间存在内阻、容量、电压等差异[1 ,2 ] .在实际应用中,电池组内的单个电池容易散热不均匀或过度充电和放电.随着时间的推移,这些处于恶劣工作条件下的电池可能会提前损坏,并且电池组的整体寿命大大缩短.锂电池的安全使用仍然是一个问题,直接影响其容量和寿命的利用效率.为了确保动力电池安全可靠的运行,准确估计锂电池荷电状态(state of charge,SOC)对于能量和安全管理至关重要.目前荷电状态估算方法有安时积分、神经网络、粒子滤波、卡尔曼滤波及其改进算法等[3 ,4 ,5 ,6 ,7 ] .温度对于锂电池具有极大影响,中国大部分地区一年温差超过30 ℃,在实际使用中,动力锂电池必须考虑温度的影响. ...
Open circuit voltage and state of charge relationship functional optimization for the working state monitoring of the aerial lithium-ion battery pack
1
2018
... 随着新能源产业的发展,锂离子电池的使用需求日益增长.与一些传统的如铅酸、镍镉等电池相比,锂电池具有能量高、自放电率低、快速充放电、无毒、无记忆效应、循环寿命长等优点.锂电池在新能源汽车、航空和配电储能系统等电源应用场景中发挥着重要作用.尽管锂电池具有很多优点,但它们也受到诸如电池材料和当前制造工艺的因素的限制,导致单体锂电池之间存在内阻、容量、电压等差异[1 ,2 ] .在实际应用中,电池组内的单个电池容易散热不均匀或过度充电和放电.随着时间的推移,这些处于恶劣工作条件下的电池可能会提前损坏,并且电池组的整体寿命大大缩短.锂电池的安全使用仍然是一个问题,直接影响其容量和寿命的利用效率.为了确保动力电池安全可靠的运行,准确估计锂电池荷电状态(state of charge,SOC)对于能量和安全管理至关重要.目前荷电状态估算方法有安时积分、神经网络、粒子滤波、卡尔曼滤波及其改进算法等[3 ,4 ,5 ,6 ,7 ] .温度对于锂电池具有极大影响,中国大部分地区一年温差超过30 ℃,在实际使用中,动力锂电池必须考虑温度的影响. ...
混合动力汽车磷酸铁锂动力电池建模与SOC计算
1
2018
... 随着新能源产业的发展,锂离子电池的使用需求日益增长.与一些传统的如铅酸、镍镉等电池相比,锂电池具有能量高、自放电率低、快速充放电、无毒、无记忆效应、循环寿命长等优点.锂电池在新能源汽车、航空和配电储能系统等电源应用场景中发挥着重要作用.尽管锂电池具有很多优点,但它们也受到诸如电池材料和当前制造工艺的因素的限制,导致单体锂电池之间存在内阻、容量、电压等差异[1 ,2 ] .在实际应用中,电池组内的单个电池容易散热不均匀或过度充电和放电.随着时间的推移,这些处于恶劣工作条件下的电池可能会提前损坏,并且电池组的整体寿命大大缩短.锂电池的安全使用仍然是一个问题,直接影响其容量和寿命的利用效率.为了确保动力电池安全可靠的运行,准确估计锂电池荷电状态(state of charge,SOC)对于能量和安全管理至关重要.目前荷电状态估算方法有安时积分、神经网络、粒子滤波、卡尔曼滤波及其改进算法等[3 ,4 ,5 ,6 ,7 ] .温度对于锂电池具有极大影响,中国大部分地区一年温差超过30 ℃,在实际使用中,动力锂电池必须考虑温度的影响. ...
混合动力汽车磷酸铁锂动力电池建模与SOC计算
1
2018
... 随着新能源产业的发展,锂离子电池的使用需求日益增长.与一些传统的如铅酸、镍镉等电池相比,锂电池具有能量高、自放电率低、快速充放电、无毒、无记忆效应、循环寿命长等优点.锂电池在新能源汽车、航空和配电储能系统等电源应用场景中发挥着重要作用.尽管锂电池具有很多优点,但它们也受到诸如电池材料和当前制造工艺的因素的限制,导致单体锂电池之间存在内阻、容量、电压等差异[1 ,2 ] .在实际应用中,电池组内的单个电池容易散热不均匀或过度充电和放电.随着时间的推移,这些处于恶劣工作条件下的电池可能会提前损坏,并且电池组的整体寿命大大缩短.锂电池的安全使用仍然是一个问题,直接影响其容量和寿命的利用效率.为了确保动力电池安全可靠的运行,准确估计锂电池荷电状态(state of charge,SOC)对于能量和安全管理至关重要.目前荷电状态估算方法有安时积分、神经网络、粒子滤波、卡尔曼滤波及其改进算法等[3 ,4 ,5 ,6 ,7 ] .温度对于锂电池具有极大影响,中国大部分地区一年温差超过30 ℃,在实际使用中,动力锂电池必须考虑温度的影响. ...
基于无迹卡尔曼滤波的锂离子电池SOC估计
1
2018
... 随着新能源产业的发展,锂离子电池的使用需求日益增长.与一些传统的如铅酸、镍镉等电池相比,锂电池具有能量高、自放电率低、快速充放电、无毒、无记忆效应、循环寿命长等优点.锂电池在新能源汽车、航空和配电储能系统等电源应用场景中发挥着重要作用.尽管锂电池具有很多优点,但它们也受到诸如电池材料和当前制造工艺的因素的限制,导致单体锂电池之间存在内阻、容量、电压等差异[1 ,2 ] .在实际应用中,电池组内的单个电池容易散热不均匀或过度充电和放电.随着时间的推移,这些处于恶劣工作条件下的电池可能会提前损坏,并且电池组的整体寿命大大缩短.锂电池的安全使用仍然是一个问题,直接影响其容量和寿命的利用效率.为了确保动力电池安全可靠的运行,准确估计锂电池荷电状态(state of charge,SOC)对于能量和安全管理至关重要.目前荷电状态估算方法有安时积分、神经网络、粒子滤波、卡尔曼滤波及其改进算法等[3 ,4 ,5 ,6 ,7 ] .温度对于锂电池具有极大影响,中国大部分地区一年温差超过30 ℃,在实际使用中,动力锂电池必须考虑温度的影响. ...
基于无迹卡尔曼滤波的锂离子电池SOC估计
1
2018
... 随着新能源产业的发展,锂离子电池的使用需求日益增长.与一些传统的如铅酸、镍镉等电池相比,锂电池具有能量高、自放电率低、快速充放电、无毒、无记忆效应、循环寿命长等优点.锂电池在新能源汽车、航空和配电储能系统等电源应用场景中发挥着重要作用.尽管锂电池具有很多优点,但它们也受到诸如电池材料和当前制造工艺的因素的限制,导致单体锂电池之间存在内阻、容量、电压等差异[1 ,2 ] .在实际应用中,电池组内的单个电池容易散热不均匀或过度充电和放电.随着时间的推移,这些处于恶劣工作条件下的电池可能会提前损坏,并且电池组的整体寿命大大缩短.锂电池的安全使用仍然是一个问题,直接影响其容量和寿命的利用效率.为了确保动力电池安全可靠的运行,准确估计锂电池荷电状态(state of charge,SOC)对于能量和安全管理至关重要.目前荷电状态估算方法有安时积分、神经网络、粒子滤波、卡尔曼滤波及其改进算法等[3 ,4 ,5 ,6 ,7 ] .温度对于锂电池具有极大影响,中国大部分地区一年温差超过30 ℃,在实际使用中,动力锂电池必须考虑温度的影响. ...
基于PNGV模型和高斯-厄米特滤波的SOC估算研究
1
2017
... 随着新能源产业的发展,锂离子电池的使用需求日益增长.与一些传统的如铅酸、镍镉等电池相比,锂电池具有能量高、自放电率低、快速充放电、无毒、无记忆效应、循环寿命长等优点.锂电池在新能源汽车、航空和配电储能系统等电源应用场景中发挥着重要作用.尽管锂电池具有很多优点,但它们也受到诸如电池材料和当前制造工艺的因素的限制,导致单体锂电池之间存在内阻、容量、电压等差异[1 ,2 ] .在实际应用中,电池组内的单个电池容易散热不均匀或过度充电和放电.随着时间的推移,这些处于恶劣工作条件下的电池可能会提前损坏,并且电池组的整体寿命大大缩短.锂电池的安全使用仍然是一个问题,直接影响其容量和寿命的利用效率.为了确保动力电池安全可靠的运行,准确估计锂电池荷电状态(state of charge,SOC)对于能量和安全管理至关重要.目前荷电状态估算方法有安时积分、神经网络、粒子滤波、卡尔曼滤波及其改进算法等[3 ,4 ,5 ,6 ,7 ] .温度对于锂电池具有极大影响,中国大部分地区一年温差超过30 ℃,在实际使用中,动力锂电池必须考虑温度的影响. ...
基于PNGV模型和高斯-厄米特滤波的SOC估算研究
1
2017
... 随着新能源产业的发展,锂离子电池的使用需求日益增长.与一些传统的如铅酸、镍镉等电池相比,锂电池具有能量高、自放电率低、快速充放电、无毒、无记忆效应、循环寿命长等优点.锂电池在新能源汽车、航空和配电储能系统等电源应用场景中发挥着重要作用.尽管锂电池具有很多优点,但它们也受到诸如电池材料和当前制造工艺的因素的限制,导致单体锂电池之间存在内阻、容量、电压等差异[1 ,2 ] .在实际应用中,电池组内的单个电池容易散热不均匀或过度充电和放电.随着时间的推移,这些处于恶劣工作条件下的电池可能会提前损坏,并且电池组的整体寿命大大缩短.锂电池的安全使用仍然是一个问题,直接影响其容量和寿命的利用效率.为了确保动力电池安全可靠的运行,准确估计锂电池荷电状态(state of charge,SOC)对于能量和安全管理至关重要.目前荷电状态估算方法有安时积分、神经网络、粒子滤波、卡尔曼滤波及其改进算法等[3 ,4 ,5 ,6 ,7 ] .温度对于锂电池具有极大影响,中国大部分地区一年温差超过30 ℃,在实际使用中,动力锂电池必须考虑温度的影响. ...
Two-layer online state-of-charge estimation of lithium-ion battery with current sensor bias correction
1
2019
... 随着新能源产业的发展,锂离子电池的使用需求日益增长.与一些传统的如铅酸、镍镉等电池相比,锂电池具有能量高、自放电率低、快速充放电、无毒、无记忆效应、循环寿命长等优点.锂电池在新能源汽车、航空和配电储能系统等电源应用场景中发挥着重要作用.尽管锂电池具有很多优点,但它们也受到诸如电池材料和当前制造工艺的因素的限制,导致单体锂电池之间存在内阻、容量、电压等差异[1 ,2 ] .在实际应用中,电池组内的单个电池容易散热不均匀或过度充电和放电.随着时间的推移,这些处于恶劣工作条件下的电池可能会提前损坏,并且电池组的整体寿命大大缩短.锂电池的安全使用仍然是一个问题,直接影响其容量和寿命的利用效率.为了确保动力电池安全可靠的运行,准确估计锂电池荷电状态(state of charge,SOC)对于能量和安全管理至关重要.目前荷电状态估算方法有安时积分、神经网络、粒子滤波、卡尔曼滤波及其改进算法等[3 ,4 ,5 ,6 ,7 ] .温度对于锂电池具有极大影响,中国大部分地区一年温差超过30 ℃,在实际使用中,动力锂电池必须考虑温度的影响. ...
An online state of charge estimation algorithm for lithium-ion batteries using an improved adaptive cubature Kalman filter
1
2018
... 随着新能源产业的发展,锂离子电池的使用需求日益增长.与一些传统的如铅酸、镍镉等电池相比,锂电池具有能量高、自放电率低、快速充放电、无毒、无记忆效应、循环寿命长等优点.锂电池在新能源汽车、航空和配电储能系统等电源应用场景中发挥着重要作用.尽管锂电池具有很多优点,但它们也受到诸如电池材料和当前制造工艺的因素的限制,导致单体锂电池之间存在内阻、容量、电压等差异[1 ,2 ] .在实际应用中,电池组内的单个电池容易散热不均匀或过度充电和放电.随着时间的推移,这些处于恶劣工作条件下的电池可能会提前损坏,并且电池组的整体寿命大大缩短.锂电池的安全使用仍然是一个问题,直接影响其容量和寿命的利用效率.为了确保动力电池安全可靠的运行,准确估计锂电池荷电状态(state of charge,SOC)对于能量和安全管理至关重要.目前荷电状态估算方法有安时积分、神经网络、粒子滤波、卡尔曼滤波及其改进算法等[3 ,4 ,5 ,6 ,7 ] .温度对于锂电池具有极大影响,中国大部分地区一年温差超过30 ℃,在实际使用中,动力锂电池必须考虑温度的影响. ...
A comparative study of different equivalent circuit models for estimating state-of-charge of lithium-ion batteries
0
2018