近年来，我国大力发展新能源汽车，新能源装机容量占比日益提高^[1]。新能源电动汽车作为可持续交通系统的重要组成部分，是我国实施节能减排的重要举措。然而动力电池技术是目前制约电动车辆发展的关键瓶颈问题^[2]，其直接影响到电池汽车续航里程、充放电技术和安全性等问题。动力电池技术是一个多领域、多学科问题，动力电池化学反应过程较为复杂，受外部环境：如温度、充放电倍率；内部结构：如材料、几何尺寸等多因素影响。一直以来，如何表征电池特性是学术界研究的重点和难点，目前常用的表征电池特性模型^[3]有电化学模型和等效电路模型。电化学模型^[4,5]是通过微分方程对电池工作时内部产生的化学反应进行描述，其模型的精度依赖所建立的微分方程，但电池内部的化学反应十分复杂，几乎无法完全考虑，因此电化学模型多应用于实验室研究。等效电路模型辨识简单，是目前使用最广泛的电池模型，使用可控电压源描述电池的热力学平衡电势，RC并联网络描述电池的动力学特性。国内外学者对等效电路模型^{[6,7,8,9,10,11,12]}进行了一些研究，并取得一些成果。Barai等^[7]提出零状态滞后模型，考虑滞回测试过程中容量以及时间变化的问题，通过4种不同锂电池进行滞回特性的评估，结果表明滞回现象仅发生在放电快结束时。孙涛等^[8]根据动力电池内部参数随负载变化情况，基于Thevenin模型进行了最小二乘法参数辨识，未对模型进行动态特性分析。杨世春等^[9]以磷酸铁锂动力电池为对象，基于PNGV改进的等效电路模型，重点研究卡尔曼滤波法结合安时积分法估算电池荷电状态（SOC）的方法，以恒流工况和动态工况分析了回弹特性和滞回特性对SOC估计的影响，对模型的精度和复杂度的平衡情况分析不足。毕军等^[10]基于Nernst 经验模型，利用遗忘因子递推最小二乘法对模型参数进行在线辨识，解决模型参数不能通过实时数据获得的问题，工程应用性较强。熊瑞等^[11]分析了健康状态、电池种类、环境温度对动力电池模型预测精度的影响，借用AIC信息准则对n阶RC模型进行分析，得出二阶RC模型为最佳模型，并且基于数据融合的方法对二阶RC模型进行了状态估计。任晓霞等^[12]基于电池集总参数RC等效电路模型进行研究，主要考虑电池的极化效应和迟滞电压特性对二阶RC模型的预测精度的影响，未与其他模型进行分析对比。

以上模型主要通过描述输入电流和输出电压的关系来表征电池的复杂电化学过程。但随着动力电池运行工况愈加复杂，单方面考虑电池充放电电流和电压的状态，已经不足以模拟完整的电池动态运行状态。因此，本文通过分析动力电池输出电压与欧姆极化、电化学极化、浓差、不平衡电势、迟滞特性等之间的关系，结合容量、温度、倍率、迟滞、自放电等因素^[13]对运行工况的影响，提出动态的综合型等效电路模型（dynamic synthesis equivalent circuit model，DS-ECM），为进一步实现SOC估算提供一个较优的电池模型。

等效电路模型常被用来模拟电池内部复杂的电化学反应，简单的模型无法反映电池内部动态特性，而复杂的模型需要辨识较多的参量，使得计算量过大，不具有实际操作性。通过分析比较常见的几种等效电路模型，研究对应空间方程以及各自特点，为本文后续研究提供依据，具体内容如表1所示。

现研究的等效电路模型，大多是对上述模型进行改进。常用的方法是增加RC并联网络表征电池内部的动态特性，但是随着RC网络的增加，SOC估算精度并未得到较好的提高，反而增加了辨识难度、降低了辨识效率。基于二阶RC模型，从动力电池的温度特性、松弛现象^[14]与迟滞效应^[15]三个角度分别研究充电和放电过程的等效模型，引进AIC误差分析方法验证本文提出DS-ECM模型优于Rint、PNGV、二阶RC模型的观点。

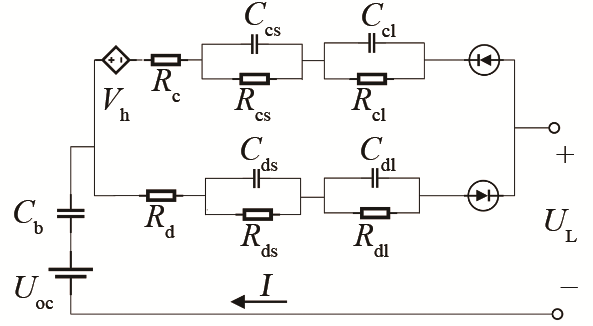
DS-ECM模型是在二阶RC模型的基础上将充电和放电回路加以区分，增加两个二极管，分别控制充放电支路导通与关断，研究充放电过程中的迟滞现象；同时分别在各支路中增加电阻（R_c、R_d），研究充放电过程中内阻的变化情况；在充电回路中增加受控电压源V_h，来表征电池迟滞电压和修正充放电过程中端电压的不一致性。完整的DS-ECM等效电路图如图1所示。

图1中，U_oc是开路电压；C_b是储能电容，表征电池稳态的变化；充放电内阻R_c、R_d与两组二阶RC并联回路，分别表征电池充放电时的极化效应；其他参数与二阶RC表示相同。

本文主要研究模型参数受负载和工况变化影响的情况，电池模型输出状态方程简要的表达见式(1)，该方程是以放电方向为正方向。

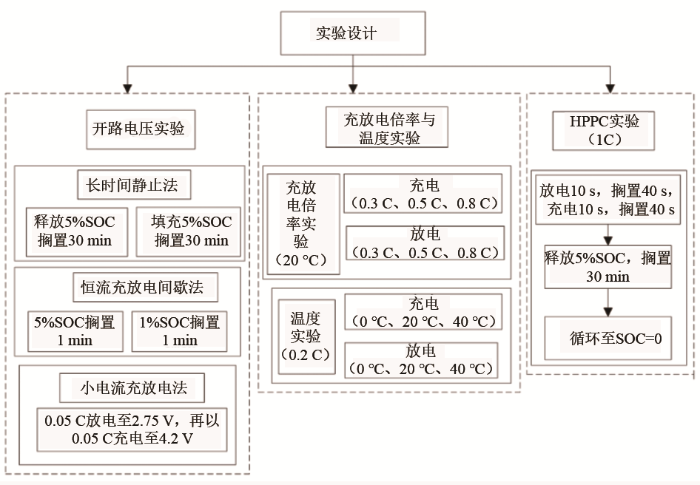
为研究电池容量、温度、倍率、迟滞、自放电等因素对动力电池模型建立的影响，分析动力电池端电压与欧姆极化、电化学极化、浓差极化、不平衡电势、迟滞特性之间的关系。本文设计了3个实验：①不同充放电倍率及搁置时间的开路电压实验；②不同充放电倍率及温度的影响因素实验；③验证模型精度的HPPC动态工况实验。具体实验步骤如图2所示。

三元锂电池俗称“三元动力电池”，正极材料由LiCoO₂、LiNiO₂、LiMnO₂三种组分构成，负极材料由石墨构成。在电化学性能上3种正极材料结构互补，性能好于单一组分正极材料电池，且具有单一组分正极材料电池的特性，能够较好地表征常规锂离子电池的特性。因此，本文以标称容量为1.8 A·h的三元锂电池作为动力锂离子电池的代表进行研究。电池的放电温度范围：0～60 ℃；充电温度：0～45 ℃；工作温度：-20～50 ℃；最佳工作温度：20～40 ℃。其中充电截止电压4.2 V，放电截止电压2.75 V。标准充电方式为先以0.3 C恒流充电至4.2 V，再以4.2 V恒压充电至截止电流2.5 A结束。

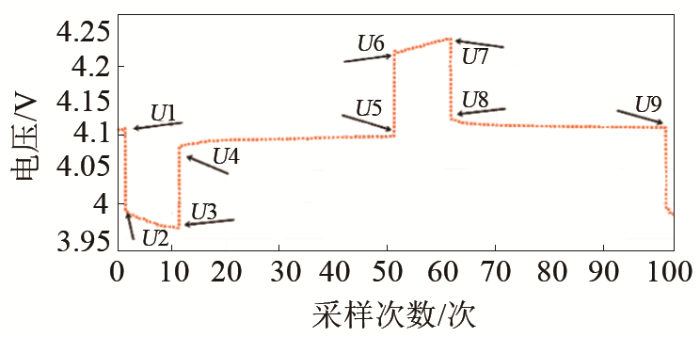
参数辨识方法可分为静态辨识与动态辨识。静态辨识是用一个固定的参数值衡量电路元件，其缺点为忽略动力电池工作时是一个动态过程，参数值会随电池SOC变化而变化。动态辨识是用一个随SOC变化的参数值衡量电路元件，参数值随负载和工况的实际情况更新，以此获取可靠的估算结果。模型参数的准确性较大程度依赖辨识的方法，考虑电池的动态特性和应用性，选用混合动力脉冲能力特性（HPPC）实验法辨识电池内部参数，分析SOC变化过程中的激励与响应之间的关系，获得动力电池DS-ECM模型参数。HPPC的实验数据样本包含电池充电、放电、搁置等过程，如图3所示。

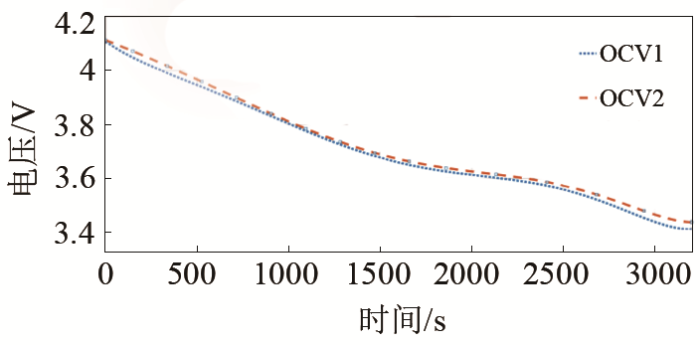
相同SOC情况下充电与放电时开路电压的差值称为迟滞电压。在工程学中把这种现象定义为迟滞效应。实验得到的充放电开路电压状态曲线如图4所示，OCV1、OCV2分别为DS-ECM模型的放电、充电时开路电压曲线。

电池的充放电过程其实是锂离子在正负极之间来回嵌入和脱出的过程。当电池放电后进行搁置时，正极上锂离子占比将会下降，负极上锂离子占比上升，这样就会造成电池放电静止后开路电压下降；反之，当电池充电后进行搁置时，电池的开路电压将会上升，使得OCV-SOC不是一一映射的关系，而是会受到电池上一时刻状态的影响，且充电时OCV2略大于放电时OCV1。

常见消除迟滞电压的方法有两种：一种是取充放电OCV平均值，然后在此基础加上或减去某个常数，但此方法补偿SOC 两端区间的OCV时误差较大；另一种是把迟滞电压变化分成三段^[16]，对每一段分别进行线性化处理，该方法考虑了迟滞电压在两端误差较大的现象，但线性度达不到要求。综合两种方法的优点，提出通过polyfit函数^[17]对曲线进行高阶拟合，以放电时开路电压为基础，对充电时开路电压进行补偿的方法，结果如图5所示。

由图5可知，迟滞电压与SOC之间的关系：在SOC（0～0.15，0.85～1）区间，相同的SOC对应的迟滞电压较大；在SOC（0.15～0.85）区间，迟滞电压较平稳，趋于一个固定值。

为了客观反映拟合效果，利用数理统计回归分析法计算SSE、R-square、Adjusted R-square、RMSE反应拟合程度，结果如表2所示。

由表2结果和文献[17]可知，7阶拟合曲线来修正电池的迟滞电压为最佳。

由图3可知，电池在充放电开始瞬间电压会瞬间降低或升高，主要由电池内部欧姆极化导致。在DS-ECM模型上反映为充放电内阻的不一致性上，即放电内阻R_d和充电内阻R_c不相同。根据欧姆定律可求R_d、R_c，见式(2),(3)。

电池在充放电过程中存在严重的极化效应，主要包括瞬时欧姆内阻极化和稳态电化学极化。DS-ECM模型使用4组RC网络分别表征充、放电过程中的电池的浓差极化与活化极化。以放电作为研究过程，在U₄～U₅阶段，RC回路为零输入响应，如式4所示。

使用Cftool工具箱对U₄-U₅段变化曲线进行拟合，可求得U_s(0)、U_l(0)、τ_s、τ_l。

电池搁置1 h后得U₂，内部极化效应基本消失。因此U₂～U₃段视为零状态响应，极化电容两端电压为

U₃点到U₄点的瞬间电池极化电压基本不变，由此可得：

式中，t_s是U₂到U₃放电脉冲的时间。将已求的Us(0)、Ul(0)、τ_s、τ_l代入式(7),(8)可以求得R_s和R_l，然后再根据时间常数表达式求出C_s、C_l。

根据2.2节的方法，将开路电压、温度、倍率和充放电实验数据作为影响模型参数的外部因素，对DS-ECM模型所有参数进行修正。f(x)=p₀x⁷+p₁x⁶+p₂x⁵+p₃x⁴+p₄x³+p₅x²+p₆x+p₇，式中，x为SOC，f(x)为待拟合参数曲线，p₀、p₁、p₂、p₃、p₄、p₅、p₆、p₇为辨识参数的系数，结果如表3所示。

为了验证DS-ECM模型优于Rint、PNGV、二阶RC模型，针对温度变化的工况进行模拟仿真，对比分析4种模型动态变化情况。选取10 ℃下的HPPC测试数据对4种模型仿真，端电压动态变化仿真结果如图6所示，充电过程端电压变化如图7所示，仿真结果与理论值误差如图8所示。

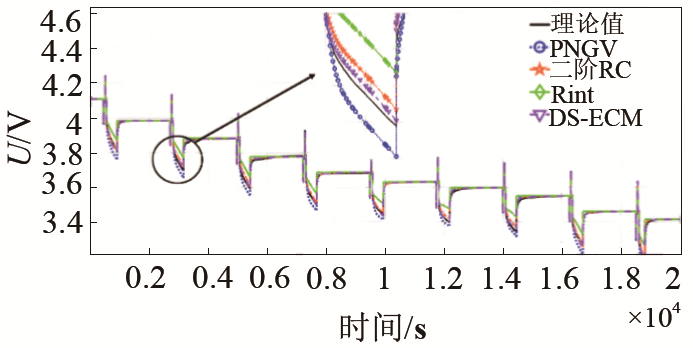
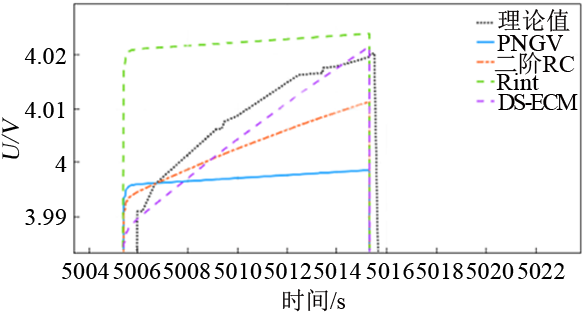
由图6可知，Rint模型估计值比理论值偏大，因为Rint模型只考虑欧姆极化效应，未考虑电化学极化造成的电池内部的电压损耗，因此无法体现动态工作过程。PNGV模型估计值比理论值偏小，因为PNGV模型用一组RC网络表征活化极化和浓差极化，未考虑活化极化和浓差极化随工况变化速率不同，单一的RC网络无法表征两种极化现象，导致拟合的电压损耗大于电池内部实际电压损耗。二阶RC和DS-ECM模型在放电过程中的拟合值接近于理论值，因为充分考虑了电池内部的极化效应。

由图7可知，充电过程中，二阶RC模型平均误差为15.2 mV，相对误差为1.94%；DS-ECM模型平均误差为5 mV，相对误差为1.31%。DS-ECM模型比二阶RC模型平均误差降低67.1%。因为二阶RC模型未考虑充、放电过程中电池内部电解液分解速度变化情况，将放电过程中OCV-SOC的关系映射到充电过程。DS-ECM模型在考虑了充、放电过程的迟滞效应基础上增加了修正电压V_h，使得图7中仿真效果为最佳。

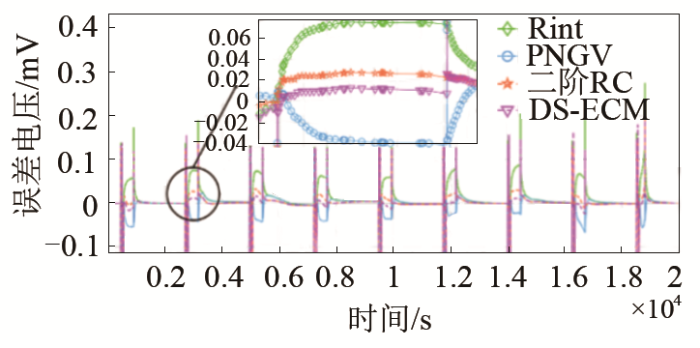
由图8可知，Rint和PNGV模型产生误差较大。二阶RC模型放电过程中平均误差为24.1 mV，相对误差为1.6%；DS-ECM模型放电过程中平均误差为11.5 mV，相对误差为0.84%。DS-ECM模型比二阶RC模型的平均误差降低了52.3%，因为DS-ECM模型的参数的值是动态的，随负载和工况的变化而变化，能够很好的消除迟滞电压、温度等外部因素对端电压估算的影响。

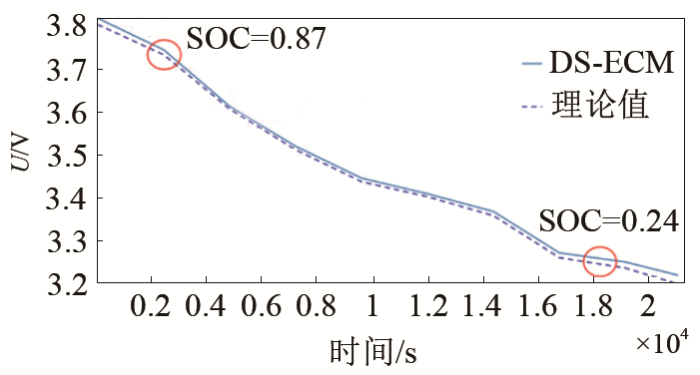
在动态工况下，完整的一次充放电视为动力电池的全寿命周期。为验证该模型对三元锂离子电池在整个生命周期过程中的驱动能力，以放电为例，每次放电开始至5 min后取一个端电压数据点，将DS-ECM模型仿真的值与理论值拟合比较，结果如图9所示。

由图9可知，可将动态工况放电过程分为两个阶段：可靠的模拟阶段，在SOC值为1～0.87和0.24～0区间；精准模拟阶段，在SOC值为0.87～0.24区间。对三元锂离子电池而言，DS-ECM模型在全寿命周期精准模拟存在不足，但整个放电过程的模拟误差相对较小。

借用赤池信息准则（AIC）分析方法对Rint、PNGV、二阶RC和DS-ECM模型的复杂度与准确度进行客观评价。AIC是衡量统计模型拟合优良性的一种标准，在评估模型中AIC表达方式如式(9)所示

式中，k是参数的数量；n为观察数；e2为残差平方和。

根据式(9)分别对Rint、PNGV、二阶RC和DS-ECM模型求AIC、最大误差、平均误差和辨识时间，结果如表4所示。

由于AIC是模型欠佳的指标，AIC最小值对应的模型视为最佳模型。由表4可知，PNGV模型的AIC最小，为最理想模型。因为PNGV相比Rint模型提高了精度，相比较二阶RC与DS-ECM模型减少了参量的个数，降低了模型的复杂度。

由于AIC值并不能完全反映电池模型的适合度，必须从最大误差、平均误差、仿真时间综合考虑电池模型的优良。DS-ECM较PNGV模型的最大误差降低了72%，平均误差降低71%，而AIC值和辨识时间增加相对较少。综上所述，DS-ECM模型优于其余几种模型，是精度和结构复杂度最佳的平衡模型。

文中针对1.8 A·h的三元锂电池，做了以下研究：①充、放过程中开路电压、温度、倍率等因素的基础实验和多因素的混合动力脉冲能力特性实验；②基于二阶RC模型提出DS-ECM模型；③对模型进行辨识，并提出7阶拟合修正参数方法；④验证模型的自适应性。最后得到以下结论。

（1）除欧姆极化、电化学极化外，浓差极化、温度变化、不平衡电势、迟滞特性对电池端电压也有影响。DS-ECM比二阶RC模型的平均误差降低了52.3%。

（2）DS-ECM模型提高精度的情况下，AIC值和计算量相对适中，能够应用于实际工程中。

总之，研究所提出的DS-ECM模型，综合考虑多因素不确定性，建立动力电池等效电路模型，能够准确地表征动力电池的电化学反应之外，实时性也较好。能够解决电池汽车续航里程、充放电技术和安全性电学模型研究问题，促进动力电池在能源结构上优化升级，实现清洁低碳发展。