近年来,新能源汽车得到了普遍的认可和广泛的使用。数据显示,2019年我国新能源汽车产量达124.2万辆,其中纯电动汽车102万辆,插电式混合动力汽车23.2万辆;预计到2020年底,我国新能源汽车保有量将达585.27万辆[1]。2019年全年,我国动力电池装机量高达62.38 GW·h,主要为三元锂电池及磷酸铁锂电池。锂电池作为当前新能源汽车的主要能量源,拥有低污染、高能量密度、高功率密度及长循环寿命等优势[2-3]。但由于电动汽车的使用工况复杂多变,容易造成锂电池组过流、过压、过充及过放等问题。这将会降低车辆续驶里程和加速电池老化,造成动力电池组过热甚至出现燃烧或爆炸等恶性事故。因此,有效的电池管理系统(battery management system,BMS)是电动车辆安全、高效运行的关键。
电池管理系统通过监测电池组运行中电压、电流及温度等数据,对电池内部状态进行估计,最终实现充放电控制、热管理及故障诊断等功能。因此,精确、高效的电池模型对于电池管理系统的功能实现极其重要。本文面向电池管理系统,针对电动汽车锂电池建模方法展开综述,重点描述适用于电池管理系统的锂电池建模方法及模型应用。
1 电池管理系统介绍
1.1 电池管理系统基本功能
受锂电池的能量密度所限,目前电动汽车行驶时的能量由数百节单体电池组成的电池组提供,电动汽车都需配备电池管理系统。电池管理系统的主要任务是:保障电池组在适宜工作条件下高效运行,从电池系统的安全性、耐久性及动力性三方面发挥作用。其主要功能如下[4]。
(1)参数监测。包括总电压、总电流、单体电池电压监测、温度监测、烟雾监测、绝缘监测及碰撞监测等。
(2)状态估计。包括荷电状态(state of charge,SOC)、健康状态(state of health,SOH)及故障安全状态(state of safety,SOS)等。
(3)充电控制。根据监测值及估计值,对电池充电电压、电流进行管理,避免过充、过放及过热等问题。
(4)电池均衡[5]。根据电池信息,采用主动或被动、耗散或非耗散等均衡方式,减小电池组的不一致性。
(5)热管理。根据电池组内温度信息及充放电需求,决定主动加热或散热的时机和强度,使得电池尽可能工作在最适合的温度,充分发挥电池的性能。
(6)网络通信。与整车控制器等网络节点进行通信,实现在线标定、监控、自动代码生成和程序下载等功能。
(7)数据存储。存储关键数据用于后续分析、标定及算法改进。
1.2 电池管理系统基本结构
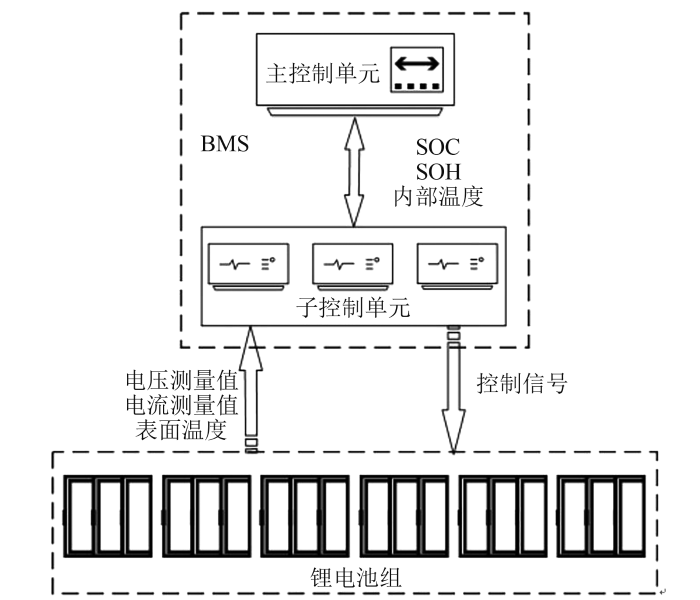
电池管理系统的结构主要有分散式结构及模组式结构[6]。分散式结构中各电池单体均配有监控模块,其结构简单且能及时掌握各单体电池的状态,安全性较高;但其模块较多,容易引起数据丢失等问题,系统效率及稳定性较差。模组式结构将电池组分解为多个模组,并由主控单元对各电池模组分别监控、管理。该结构采集精度高、可靠性好且拓展性强,适用于电动汽车等电池数量较多的电池系统。
图1
图1
电池管理系统功能及结构
Fig.1
Diagram of function and structure of battery management system
2 锂电池建模方法
根据模型中参数处理方法的不同,锂电池模型主要分为电学特性模型、热模型及电-热耦合模型。
2.1 电学特性模型
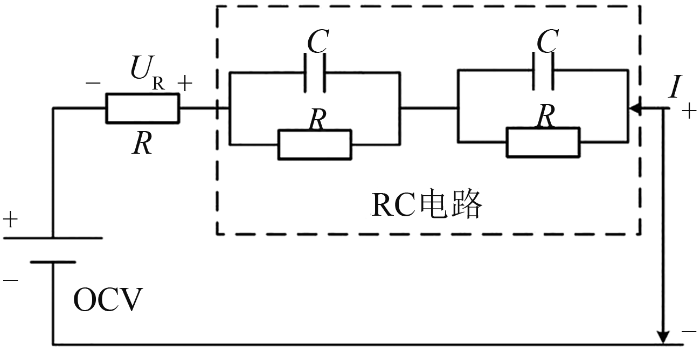
等效电路模型使用电压源、电阻及电容等组成电路,用来模拟锂电池的动态特性。典型的等效电路模型框架如图2所示。
图2
2.2 热模型
均匀参数热模型假设电池内部产热均匀,将锂电池整体或其内部某区域视为均匀热源。其生热量计算通常基于Bernardi等[23]提出的电池内部均匀发热模型,常规充放电条件下生热速率为
式中,q为电池生热速率;I为充放电电流;V为电池生热域的体积;Uoc为开路电压;U为电池工作电压;T为电池温度;∂Uoc/∂T为电池开路电压受温度影响的系数。
在此模型基础上,许多研究人员对电池热量生成、积累、传导和对流进行解释[24],并对电池单体及模组的热行为进行模拟、预测及管理。雷治国等[25]以35 A·h方形锰酸锂电池为对象,对电池充放电生热特性进行建模仿真和试验,结果表明随着放电电流增大,电池温升快速提高,可在低温环境下利用电池放电生热以改善电池性能。Gümüssu等[26]针对松下18650B型锂电池建立了三维CFD模型,在假设电池为均匀热源的情况下研究了电池在自然对流状态下的生热及对流换热问题。张彩萍等[14]假设电池表面温度分布均匀,使用平均电容作为计算参数,提出一种改进的生热模型并将其应用于电动汽车快充策略优化,使充电时间缩短50%。均匀参数热模型因忽略电池内部温度分布,多用于小型电池低倍率充放电工况及实际工程。
分布参数热模型认为电池内部产热不均匀,依据电池内部电流密度与温度的关系计算电池温度分布。基于电流密度的生热率q、电流密度J的计算方法如
式中,φs、φe分别为固相以及液相中的电势;σeff为固相颗粒的电导率;keff为电化学反应速率常数;kDeff为液相离子电导率;ce为电解质浓度;cs,max为固相中插入的锂离子最大浓度;cs,surf为固相表面的锂离子浓度;F为法拉第常数;R为气体常数;η为电化学反应超电势。
此类模型能较为精确地反映电池内部的温度分布,以指导电池的材料选择及结构设计。Kim等[28]应用有限元方法对VK公司的10 A·h方包锂电池进行简化建模,分析了不同电池结构(电极长宽比、集流片位置)和放电倍率下电流密度和温度分布,并通过红外成像试验验证了模型的正确性。部分商业软件也针对电池热模型开发了应用包[29-30],但这类软件因耦合多个复杂的偏微分方程,对计算能力有较高的要求而难以在电池管理系统中应用。为此,一些降阶分布参数热模型被用于高效计算和热管理控制。Hu等[31]基于计算流体力学提出一种降阶状态空间模型,在保证计算量较小的同时能提供与CFD模型相近的结果。Richardson等[32]提出了一种考虑瞬态生热、各向异性热传导及非均匀对流边界条件的低阶二维热模型,通过与有限元计算结果的比较,验证了模型的计算效率及精度。
2.3 电-热耦合模型
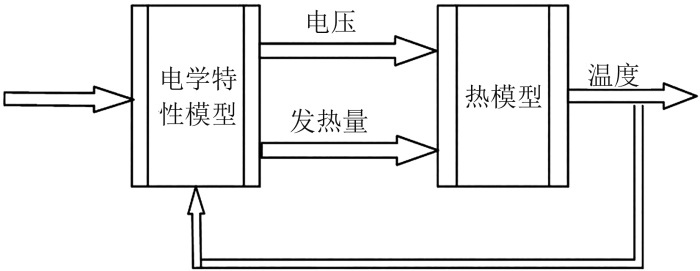
锂电池的电学效应与热特性通过发热量形成强耦合。电池温度直接影响电学特性模型的重要参数(如内阻、电压等),而这些参数同时也影响电池的发热量,其电热耦合关系如图3所示。
图3
为同时精确获得电池的电效应(例如电流、电压和SOC)和热特性(例如温度分布),学者们建立了一系列电热耦合模型。常见的电热耦合模型可分为电化学-热耦合模型及电-热耦合模型。
3 锂电池模型在BMS中的应用
由于锂电池的内部参数不能直接测量,只能借助于相关的算法对其内部状态(SOC、SOH及内部温度等)进行估计。对于电池组而言,电池单体的不一致性加剧了BMS管理的难度。因此,前述锂电池的电学特性模型、热模型及电-热耦合模型的鲁棒性对于BMS精准管理具有重要意义。
3.1 SOC估计
锂电池的荷电状态(SOC)通常是指在相同情况下,电池当前剩余容量占额定容量的百分比。精确的SOC估计能提高电池管理系统的控制效率,进而提升车辆的续驶里程。目前,对SOC的研究已较为成熟,常用的方法可分为直接评估法和基于模型的方法。
直接评估法基于对电流及电压的直接测量,又分为安时积分法及开路电压法。安时法的计算公式如下:
式中,SOC0为初始的荷电状态;η为库仑效率;i(t)为放电电流。由于安时积分法高度依赖起始状态SOC0及荷电状态误差累积效应,开路电压法因需要充分静置以达到平衡电动势耗时较长等问题,均未能有效应用于电池管理系统。因此,基于模型的SOC估计方法在电池管理系统中得到了较为广泛的应用。
3.2 SOH估计
锂电池的健康状态(SOH)是表征锂电池性能状态的重要指标,也是BMS重要的监测任务之一。其一般描述公式为
式中,SOH(t0)为电池初始的健康状态;δfunc为电池老化率函数(取决于电流、温度、SOC等因素);others为其他因素如机械振动和过电势等。目前,对锂电池SOH的评判指标主要有最大可用容量及电池内阻,估计方法主要有实验法、模型法、数据驱动法及融合法。
3.3 内部温度估计
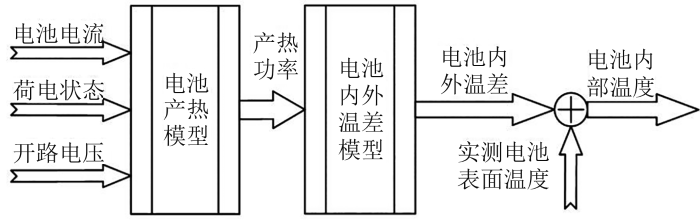
动力电池组温度对于电池容量、放电效率、循环寿命及安全性均有重要影响,因此也是BMS监测的重要内容之一。通过仪器可以直接测量电池表面的温度,为避免仪器侵入电池内部造成电解液的泄漏,故只能使用热模型进行估计。准确的内部温度估计是BMS对电池组进行加温、散热等控制的主要判断依据。
图4
图4
电池内部温度估计流程
Fig.4
Estimation process of inside temperature of lithium battery
4 结 语
本文简要介绍了车用动力电池管理系统的功能及结构。模组式电池管理系统因其采集精度高、可靠性好且拓展性强等优点,在车辆电池系统发挥着巨大作用。对适用于电池管理系统的锂电池建模方法进行梳理,表明降阶的电化学模型、等效电路模型、集中参数热模型、简化的分布参数热模型及部分电-热耦合模型能有效的应用于电池管理系统。对基于电池管理系统的建模方法在锂电池SOC估计、SOH估计及内部温度估计的应用进行了总结。
参考文献
中国新能源汽车行业发展水平分析及展望
[J].
Analysis and prospect of China's new energy vehicle industry development level
[J].
Recent developments and likely advances in lithium-ion batteries
[J].
Numerical analyses on optimizing a heat pipe thermal management system for lithium-ion batteries during fast charging
[J].
A review on the key issues for lithium-ion battery management in electric vehicles
[J].
用锂离子动力电池组均衡管理系统研究进展
[J].
Review on lithium-ion battery equilibrium technology applied for EVs
[J].
电池管理系统的设计与实现
[J].
Design and implementation of battery management system
[J].
Micro-macroscopic coupled modeling of batteries and fuel cells (I): Model development
[J].
Modeling of galvanostatic charge and discharge of the lithium polymer insertion cell
[J].
Electrochemical model of a lithium-ion battery implemented into an automotive battery management system
[J].
A framework for simplification of PDE-based lithium-ion battery models
[J].
State of charge estimation based on a simplified electrochemical model for a single LiCoO2 battery and battery pack
[J].
Identification and modelling of lithium ion battery
[J].
A comparative study of equivalent circuit models of ultracapacitors for electric vehicles
[J].
A comparative study of equivalent circuit models for Li-ion batteries
[J].
State-space model with non-integer order derivatives for lithium-ion battery
[J].
锂电池分数阶建模与荷电状态研究
[J].
Fractional model and state of charge of lithium battery
[J].
Charging optimization in lithium-ion batteries based on temperature rise and charge time
[J].
电动汽车动力电池健康状态估计方法研究
[D].
Research of state of health estimation method for electric vehicle lithium-ion power batter
[D].
Support vector machine based battery model for electric vehicles
[J].
Equivalent circuit model parameters of a high-power li-ion battery: thermal and state of charge effects
[J].
Effective modeling of temperature effects on lithium polymer cells
[C]//
基于寿命量化的混合储能系统协调控制参数优化
[J].
Optimization of coordinated control parameters for hybrid energy storage system based on life quantization
[J].
A general energy balance for battery systems
[J].
锂离子电池热管理和安全性研究
[J].
Research on thermal management and safety of Li-ion batteries
[J].
电动汽车用锂离子电池热特性和热模型研究
[J].
Research on thermal characteristics and thermal model of EVs lithium-ion battery
[J].
3-D CFD modeling and experimental testing of thermal behavior of a Li-ion battery
[J].
锂离子电池单体热模型研究动态
[J].
A review on the research of thermal models for lithium ion battery cell
[J].
Effect of electrode configuration on the thermal behavior of a lithium-polymer battery
[J].
Graphene-enhanced hybrid phase change materials for thermal management of Li-ion batteries
[J].
Controlling factors of cell design on large-format Li-ion battery safety during nail penetration
[J].
A transient reduced order model for battery thermal management based on singular value decomposition
[C]//
On-board monitoring of 2-D spatially-resolved temperatures in cylindrical lithium-ion batteries (I): Low-order thermal modeling
[J].
A pseudo three-dimensional electrochemical-thermal model of a prismatic LiFePO4 battery during discharge process
[J].
Investigation of 3-D multilayer approach in predicting the thermal behavior of 20 A·h Li-ion cells
[J].
A lumped-parameter electro-thermal model for cylindrical batteries
[J].
Coupled electrochemical thermal modelling of a novel Li-ion battery pack thermal management system
[J].
电动汽车动力电池热管理技术的研究与实现
[J].
Study and implementation of thermal management technology for the power batteries of electric vehicles
[J].
On-line battery state-of-charge estimation based on an integrated estimator
[J].
A comparative study of lumped equivalent circuit models of a lithium battery for state of charge prediction
[J].
State-of-health estimation of lithium-ion battery packs in electric vehicles based on genetic resampling particle filter
[J].
On-board state of-health monitoring of lithium-ion batteries using linear parameter-varying models
[J].
The estimation of temperature distribution in cylindrical battery cells under unknown cooling conditions
[J].
Online parameterization of lumped thermal dynamics in cylindrical lithium-ion batteries for core temperature estimation and health monitoring
[J].
锂离子电池内部温度场的传递函数在线估计
[J].
Online estimation of internal temperature fields of lithium-ion batteries using a transfer function
[J].