三元锂离子电池多目标热优化

doi:10.19799/j.cnki.2095-4239.2020.0154

三元锂离子电池多目标热优化

丁昌明^,, 文　华^,

南昌大学机电工程学院，江西南昌 330031

Multi-objective thermal optimization of ternary lithium-ion battery

DING Changming^,, WEN Hua^,

School of Mechanic & Electronic Engineering, Nanchang University, Nanchang 330031, Jiangxi, China

通讯作者: 文华,副教授，研究方向为电动汽车电池热管理，E-mail:wenhua@ncu.edu.cn。

收稿日期: 2020-04-22 修回日期: 2020-05-18 网络出版日期: 2020-10-27

基金资助:

国家自然科学基金项目. 51762034

Received: 2020-04-22 Revised: 2020-05-18 Online: 2020-10-27

作者简介 About authors

丁昌明（1993—），男，硕士研究生，研究方向为锂离子电池热分析，E-mail：329016738@qq.com。 E-mail：329016738@qq.com。

摘要

锂离子电池的产热对其安全性和寿命有很重要的影响。本文基于COMSOL Multiphysics平台，针对51 A·h三元软包层叠式锂离子电池，提出了其与电极对耦合的三维电化学-热耦合有限元分析模型，结合响应面法研究正极厚度、极板宽度、正极极耳厚度、正极极耳宽度、负极极耳厚度、负极极耳宽度6个设计参数对温度场的影响，通过线性加权组合法和随机梯度下降法，求得降低电池平均温升和最大温差的最优方案。结果表明，正极厚度对温度场影响较大，与温升正相关，但是厚度小到一定程度后影响减弱。极板宽度与极耳尺寸的增加能降低放电末期电池的温升；其数值在一定范围内时，电池的最大温差达到最小值。这套优化方案误差小于2.68%，平均温升降低2.93 ℃，最大温差降低0.596 ℃，有助于提高电池的安全性和寿命，为其他电池的多目标热优化提供了参考。

关键词： 锂离子电池 ; 电化学-热耦合模型 ; 响应面法 ; 热分析 ; 多目标优化

Abstract

The heat production of the lithium-ion battery has a very important impact on its safety and life. Based on COMSOL Multiphysics, this study proposes a three-dimensional electrochemical thermal coupled finite element analysis model for a 51 A·h laminated lithium-ion pouch battery. The effects of six design parameters on the temperature field (i.e., positive electrode thickness, plate width, positive electrode tab thickness, positive electrode tab width, negative electrode tab thickness, and negative electrode tab width) are studied using the response surface method. The linear weighted sum and random gradient descent methods are used to obtain the optimal scheme to reduce the average temperature rise and the maximum temperature difference of the battery. The average temperature rise and the maximum temperature difference of the battery can be reduced by using the random gradient descent method. The results show that the positive electrode thickness greatly influences the temperature field positively related to the temperature rise; however, the influence is weakened when the thickness is reduced to a certain extent. The increase of the plate width and the tab size can reduce the temperature rise of the battery at the end of the discharge. In addition, the maximum temperature difference of the battery reaches the minimum value within a certain range. The error of the scheme is less than 2.68%. The temperature rise is reduced by 2.93 ℃. The temperature difference is reduced by 0.596 ℃, which is helpful in improving the safety and life of the battery, and provides a reference for the multi-objective thermal optimization of other batteries.

Keywords： lithium-ion battery ; electrochemical-thermal coupling model ; response surface methodology ; thermal analysis ; multi-objective optimization

PDF (4919KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

丁昌明, 文　华. 三元锂离子电池多目标热优化[J]. 储能科学与技术, 2020, 9(6): 1961-1968

DING Changming. Multi-objective thermal optimization of ternary lithium-ion battery[J]. Energy Storage Science and Technology, 2020, 9(6): 1961-1968

锂离子电池具有比能量高、循环寿命长、自放电率低、无污染等优点，已成为电动汽车的首选电源^[1]。然而，高能量密度的锂离子电池在充放电过程中会产生大量的热，如果不能及时散热，会极大威胁其安全性。除此之外，使用过程中锂离子电池温度分布的不均匀性会导致局部过充或过放，从而减少电池的寿命，降低电池(组)性能^[2-4]。极耳是影响软包叠片式电池温度分布不均匀、局部温度过高的主要因素^[5-8]。由于锂离子电池内部反应复杂以及实验设备的限制，需要通过建立精确的仿真模型去分析电池的温度场^[9]。

当前学者通常采用一维电化学模型分析温度场^[10]或者仅研究电池表面的温度分布^[11]。张志超等^[12]三维电化学热-热耦合模型研究单个电极对的电化学特性和温度场分布，但是该模型不能够反映叠片式电池的整体温度场。与此同时，为了提高锂离子电池的安全性和寿命，需要优化单体电池的结构尺寸^[13]。Liu等^[14]利用响应面法(RSM)分析正极厚度、孔隙率、活性颗粒半径等6个方面对电池平均温升的影响并提出温升的优化方案，然而缺少均温性的分析。因此本文提出电极对与电池耦合的三维电化学-热耦合模型，该模型计算量小，精度高，可与响应面法结合实现电池平均温升和最大温差的多目标优化。

1 模型介绍

1.1　电化学-热耦合模型

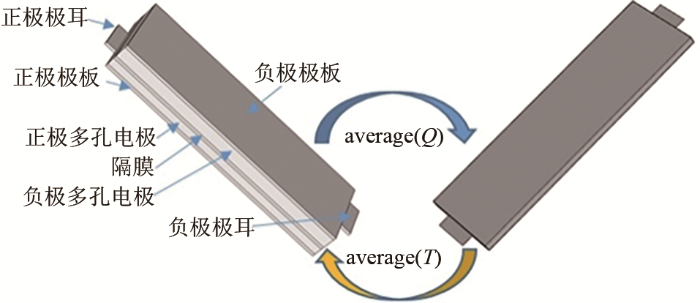
本文以恒大新能源科技集团生产的51 A·h层叠式锂离子软包电池为研究对象，该电池由53个电极对叠加而成，每个电极对都由正集流体(Al)、正极(LiNi_1/3Co_1/3Mn_1/3O₂)、隔膜(PP/PE/PP)、负极(Li_xC₆)、负集流体(Cu)组成。在放电过程中，电流从正极极耳流出，穿越隔膜以及正负极，最后流入负极。电池内部的温度场伴随着一系列复杂的化学反应和物质传输而变化。通过耦合质量、能量、电荷守恒和电化学动力学，将电极对的平均热量导入电芯中计算得到平均温度，而平均温度再反馈到电极对计算下一时刻的电芯热量，以此往复，建立起电极对和电池耦合的三维有限元模型。该模型的仿真参数以及控制方程和边界条件分别见表1、表2。由于研究1 C恒流放电的情况，因此假设正负极极耳发热量不变。模型如图1所示，左侧为电极对，为了方便观察，厚度方向做了放大处理，右侧为单体电池。

表1 仿真参数

Table 1 Parameters used in simulation

参数	单位	正极	隔膜	负极	其余	描述
L	μm	90^①	20^①	60^①		厚度
R_p	μm	3.5^①		6^①		活性颗粒粒子半径
ε₁		0.56^②		0.44^②		固相体积分数
ε₂		0.5556^②	0.4^②	0.4444^②		液相体积分数
c_1,max	mol/m³	19102^②		36100^②		最大可嵌锂浓度
c_2,0	mol/m³	1200^②	1200^②	1200^①		初始电解液锂浓度
k₀	m/s	4.38×10^-11③		1.63×10^-11③		反应速率常数
H×W×L	mm				342×109.5×9.5^①	电池长×宽×厚
TH_b	mm	0.3^①		0.2^①		极耳厚度
L_b	mm	16^①		16^①		极耳长度
W_b	mm	50^①		45^①		极耳宽度
c_p_a	J/(kg·K)				1299.4^①	电芯平均比热容
c_p_b	J/(kg·K)	900^①			385^①	极耳比热容
λ_a	W/(m·K)				1.2827^②	电芯平均热导率
λ_b	W/(m·K)	238^②		400^②		极耳热导率

①为厂家提供数据；②为计算所得数据；③为根据参考文献和基于文献调整所得。

新窗口打开| 下载CSV

表2 控制方程和边界条件

Table 2 Governing equations and boundary conditions

控制方程	边界条件
质量守恒
$\frac{\partial c_{1}}{\partial t} + \frac{1}{r^{2}} \frac{\partial}{\partial r} (- r^{2} D_{1} \frac{\partial c_{1}}{\partial r}) = 0$	${\frac{\partial c_{1}}{\partial t}\|}_{r = 0} = 0, {- D_{1} \frac{\partial c_{1}}{\partial r}\|}_{r = R_{p}} = \frac{j_{l o c}}{F}$
$ε_{2} \frac{\partial c_{2}}{\partial t} = \frac{\partial}{\partial x} (D_{2}^{e f f} \frac{\partial c_{2}}{\partial r}) + \frac{(1 - t_{+}) S_{a} j_{l o c}}{F}$	${\frac{\partial c_{2}}{\partial x}\|}_{x = 0} = {\frac{\partial c_{2}}{\partial x}\|}_{x = L} = 0$
电荷守恒
$\frac{\partial}{\partial x} (- σ_{1}^{e f f} \frac{\partial φ_{1}}{\partial x}) = - S_{a} j_{1 o c}$	${φ_{1}\|}_{x = 0} = 0, {- σ_{1}^{e f f} \frac{\partial φ_{1}}{\partial x}\|}_{x = L_{n} + L_{s} + L_{p}} = - I_{a p p}, {- σ_{1, n}^{e f f} \frac{\partial φ_{1}}{\partial x}\|}_{x = L_{n}} = {- σ_{1, p}^{e f f} \frac{\partial φ_{1}}{\partial x}\|}_{x = L_{n} + L_{s}} = 0$
$\nabla [- σ_{2}^{e f f} \nabla φ_{2} + \frac{2 R T σ_{2}^{e f f}}{F} (1 + \frac{\partial l n f_{\pm}}{\partial l n c_{2}}) (1 - t_{+}) \nabla l n c_{2}] = S_{a} j_{l o c}$	${\frac{\partial φ_{2}}{\partial x}\|}_{x = 0} = {\frac{\partial φ_{2}}{\partial x}\|}_{x = L_{n} + L_{s} + L_{p}} = 0$
电化学反应速率
$j_{l o c} = i_{0} (e x p \frac{α_{a} F η}{R T} - e x p \frac{α_{c} F η}{R T})$ , $η = φ_{1} - φ_{2} - U$ , $i_{0} = F k_{0} c_{2}^{α_{a}} {(c_{1, m a x} - c_{1, s u r f})}^{α_{a}} c_{1, s u r f}^{α_{c}}$
能量守恒
$ρ c_{p} \frac{\partial T}{\partial t} + \nabla \cdot (- λ \nabla T) = Q_{r e a} + Q_{a c t} + Q_{o h m}$ $Q_{r e a} = S_{a} j_{l o c} T \frac{\partial U}{\partial T} = S_{a} j_{l o c} T \frac{\partial S}{F}$ , $Q_{a c t} = S_{a} j_{l o c} η$ $Q_{o h m} = σ_{1}^{e f f} \nabla φ_{1} \cdot \nabla φ_{1} + [σ_{2}^{e f f} \nabla φ_{2} - \frac{2 R T σ_{2}^{e f f}}{F} (1 + \frac{\partial l n f_{\pm}}{\partial l n c_{2}}) (1 - t_{+}) \nabla (l n \nabla c_{2})] \cdot \nabla φ_{2}$	${- λ \frac{\partial T}{\partial x}\|}_{x = 0} = {- λ \frac{\partial T}{\partial x}\|}_{x = L_{n} + L_{s} + L_{p}} = h (T - T_{a m b})$

新窗口打开| 下载CSV

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 三维电化学-热耦合模型

Fig.1 Three-dimensional electrochemical-thermal coupling model

表2中，下标1指固相，2指液相，eff指有效值，n是负极，p是正极，s是隔膜；t为时间；r为活性颗粒的径向距离变量；c为浓度；φ为电势；D为扩散系数；f_±为离子迁移数；j_loc为局部电流密度；S_a为比表面积；R为通用气体常数；F为法拉第常数；α_a和α_c分别为阳极和阴极电极反应的转移系数；η为过电势；i₀为交换电流密度；U为开路电压；c_1,max为锂离子最大浓度；c_1,surf为颗粒表面的锂离子浓度；Q_rea为电化学反应热；Q_act和Q_ohm分别为极化热和欧姆热；ΔS为熵变；h为对流换热系数；T_amb为环境温度。

1.2　变量分析与优化

本文在COMSOL Multiphysics5.4平台上建立电化学-热耦合模型，获取实验点响应的温升和温差值。RSM采用Box-Behnken的实验设计方法，根据实验点的响应值将目标变量以二次多项式的近似函数模型表示，其中二次多项式模型如式(1)所示

y = A_{0} + \sum A_{i} x_{i} + \sum \sum A_{i j} x_{i} x_{j} + \sum A_{i i} x_{i i}^{2}

(1)

在Design Expert® software中通过方差分析(ANOVA)对近似函数模型进行拟合度分析。采用拟合度曲线来评价响应面拟合优度。图2和图3分别为平均温升和最大温差的残差正态分布。残差在图中基本遵循一条直线，表明复合相关系数R²靠近1，证明了近似函数模型的可靠性。

图2

新窗口打开| 下载原图ZIP| 生成PPT

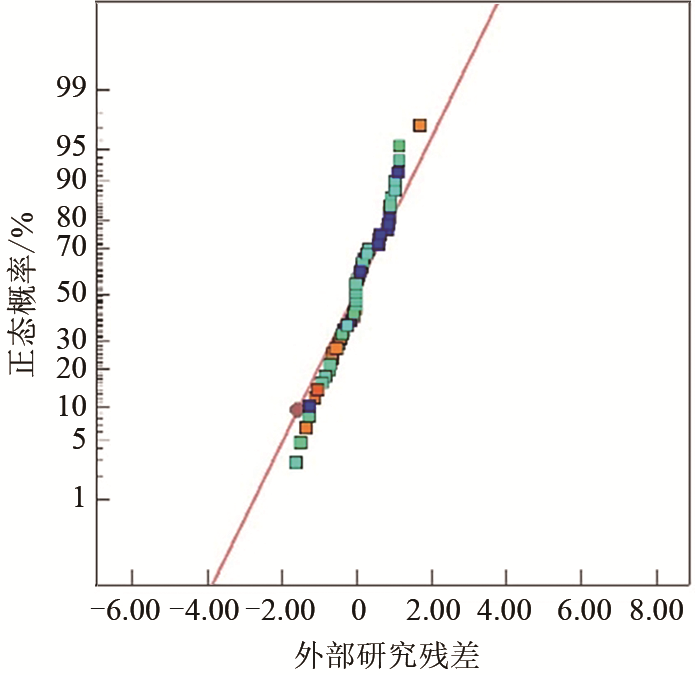
图2 平均温升残差概率分布

Fig.2 Normal probability plot of standardized residual for average temperature rise

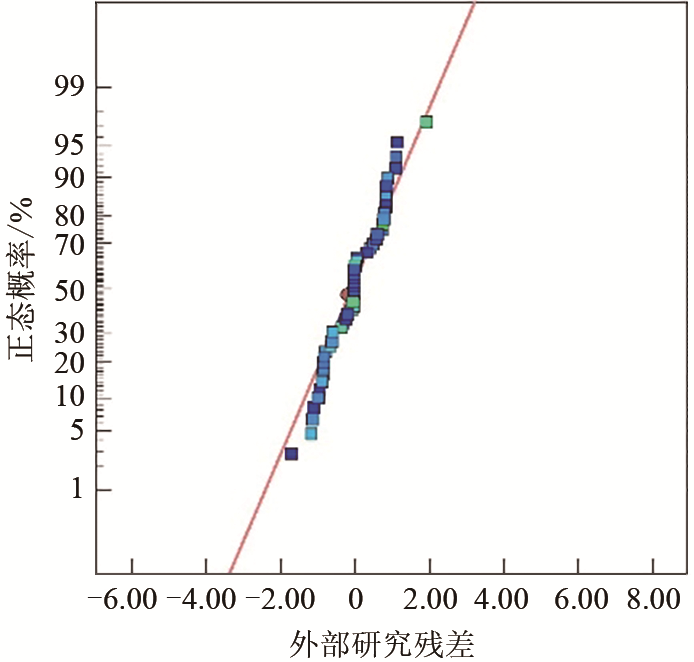
图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 最大温差残差概率分布

Fig.3 Normal probability plot of standardized residual for maximum temperature difference

基于线性加权组合法，将多目标处理成一个新的目标函数，之后从随机梯度下降法(SGD)^[15]得到的解集里找到最优解。新的目标函数如式(2)所示

m i n F (x) = {\{w^{2} {[\frac{c (x) - c_{m i n}}{c_{m a x} - c_{m i n}}]}^{2} + {(1 - w)}^{2} {[\frac{D (x) - D_{m i n}}{D_{m a x} - D_{m i n}}]}^{2}\}}^{1 / 2}

(2)

式中，c(x)和D(x)代表响应参数，max和min代表最大值和最小值；w为权值，范围在0和1之间。w值反映了响应参数的重要程度，其值越大，结果越有利于c(x)。一般w值都是根据经验所得。优化过程的响应参数是电池的平均温升T_ave和最大温差ΔT_max，这两个参数对电池寿命和安全性均有较大影响，然而现阶段没有精确数值衡量影响程度，因此本文中定性认为这两个值有同等的重要性^[16]，因此w取值为0.5。设计参数的选择要考虑成本和相关性，因此电池的设计参数包含正负极极耳的宽和厚，正极厚度以及极板的长和宽。为了不影响电池容量，在保证极板的面积是定值的基础上调整极板的长和宽来研究极板尺寸对电池产热的影响。电池放电倍率为1 C，环境温度为室温。采取六因素三水平的实验设计方案，取值范围见表3。研究设计参数的交互影响时，其他设计参数均取中等值。

表3 设计参数范围

Table 3 Range of designed parameters

因素	Level-1	Level 0	Level +1
正极厚度L_pos/μm	50	90	130
极板宽度W_p/mm	10.95	22.575	34.2
正极极耳厚度TH_pos/mm	0.1	0.4	0.7
正极极耳宽度W_pos/mm	30	60	90
负极极耳厚度TH_neg/mm	0.1	0.4	0.7
负极极耳宽度W_neg/mm	30	60	90

新窗口打开| 下载CSV

1.3　验证实验设计

将电池置于温度为(25±2)℃的高低温防爆箱中，并将正负极耳连接至5 V/300 A恒翼能动力电池测试系统。将T型热电偶贴在电池表面，利用多路温度记录仪测量电池表面温度。图4为电池的热电偶布置。用0.33 C(16.8 A)的恒流充电至电压达到4.25 V，然后用4.25 V的恒流充电至充电电流小于2.5 A(C/20)。静置1 h。将充满电的电池以1 C放电速率放电，直至电压达到2.5 V。根据电池温度的实验数据，采用文献[17]中的静温降法计算对流换热系数h，其值为5.14 W/(m²·K)。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 热电偶位置分布

Fig.4 Thermocouple position distribution

2 结果与分析

2.1　模型验证

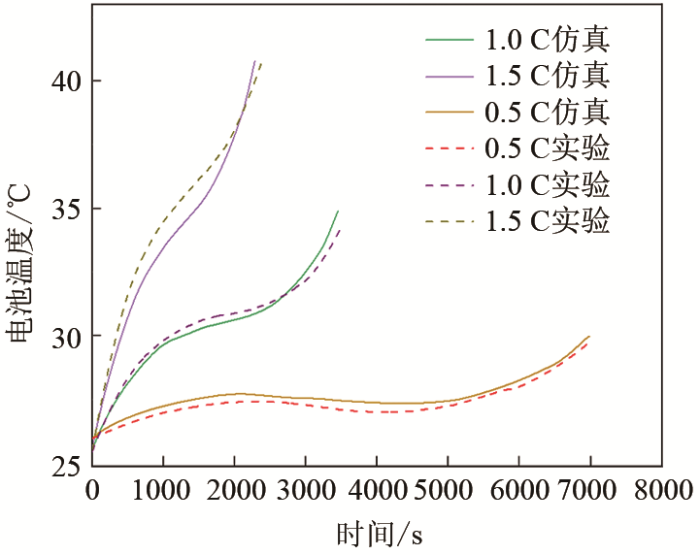
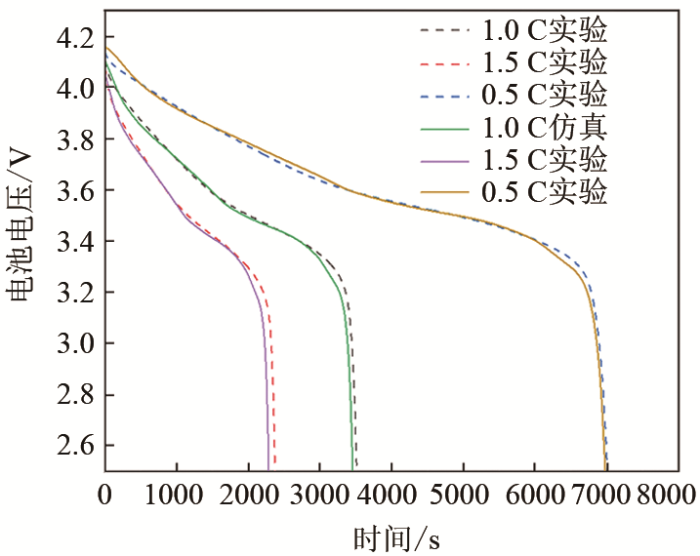
由于电池内部反应复杂，内部参数变化难以用实验设备直接测量，因此本文使用电池的电压和温度变化曲线来验证电化学-热耦合模型的准确性。图5和图6分别为电池在室温下，以0.5 C、1 C、1.5 C的恒流放电的放电电压仿真与实验结果对比和温升仿真与实验结果对比，误差随着放电倍率增加而略微增加，最大相对误差为3.08%，其余绝大部分相对误差在1.5%以内，低于实验误差所允许的5%以内^[14]。可以看出仿真和实验结果一致性较好，模型的准确性得到了验证。模型与实验的微小偏差是由于参数设置的结果，例如正负极反应速率常数来源于参考文献，与实际情况略微有所偏差，影响电池的极化程度，使得偏离量随着放电倍率增加而增加，最终导致上述误差。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 仿真与实验温度数据

Fig.5 Simulation and experimental temperature data

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 仿真与实验电压数据

Fig.6 Simulation and experimental voltage data

2.2　RSM分析

表4是实验因素的局部灵敏度表，其中p来源于ANOVA，它的大小反映对响应参数的灵敏程度，其值越小影响结果越大。在本文中当p值小于0.05时，该因素的影响是显著的。当p值小于0.01时，该因素极其显著。对电池平均温升而言，A、B、C、D、E、F、AB、AC、AF、CF的影响极为显著。对电池的最大温差而言，AC影响显著，A、AF、CF影响极为显著。图7与图8分别为上述重要因素对响应参数的交互影响等值线。

表4 局部灵敏度

Table 4 Local sensitivity

实验因素	温升p值	显著性	温差p值	显著性
A(正极厚度)	<0.0001	极其显著	<0.0001	极其显著
B(极板宽度)	<0.0001	极其显著	0.4326
C(正极极耳厚度)	<0.0001	极其显著	0.1331
D(正极极耳宽度)	0.0037	极其显著	0.4960
E(负极极耳厚度)	0.0021	极其显著	0.2772
F(负极极耳宽度)	<0.0001	极其显著	0.0623
AB	0.0031	极其显著	0.9684
AC	0.0009	极其显著	0.0292	显著
AD	0.4102		0.9823
AE	0.1055		0.3880
AF	<0.0001	极其显著	0.0088	极其显著
BC	0.9222		0.8661
BD	0.6964		0.9646
BE	0.8901		0.7789
BF	0.2878		0.8089
CD	0.0875		0.5649
CE	1.0000		0.3988
CF	<0.0001	极其显著	0.0100	极其显著
DE	0.9222		0.8547
DF	0.0592		0.4580
EF	0.0875		0.4200

新窗口打开| 下载CSV

图7

新窗口打开| 下载原图ZIP| 生成PPT

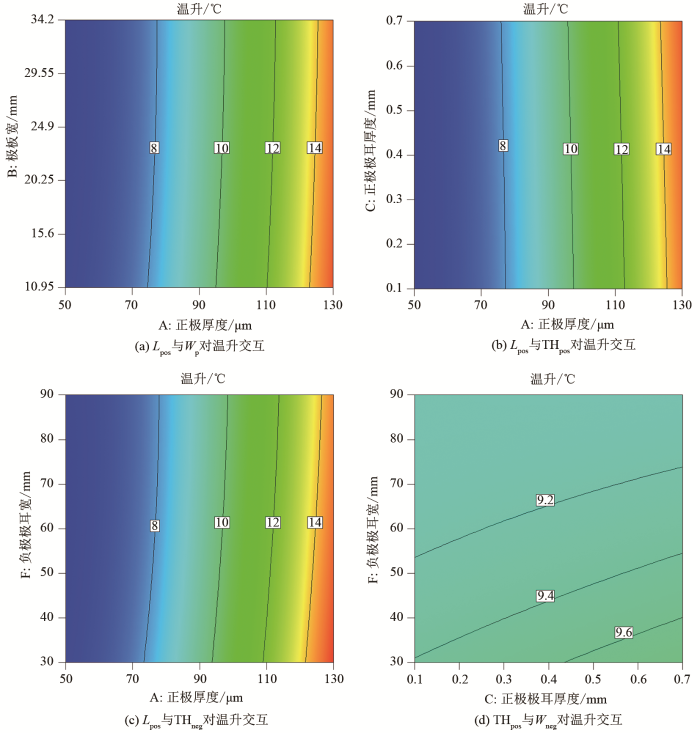
图7 重要参数对温升的交互影响等值线

Fig.7 Contour of interaction of important parameters on temperature rise

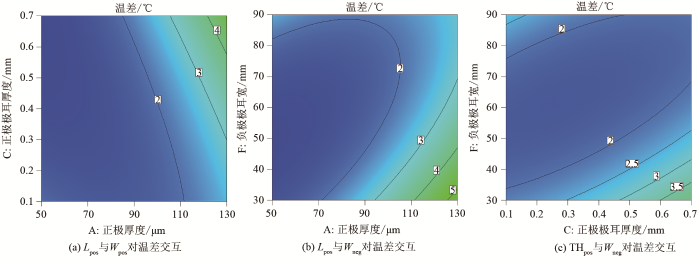
图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 正极厚度与其他参数交互对温差影响等值线

Fig.8 Contour of influence of positive electrode thickness and other parameters on temperature difference

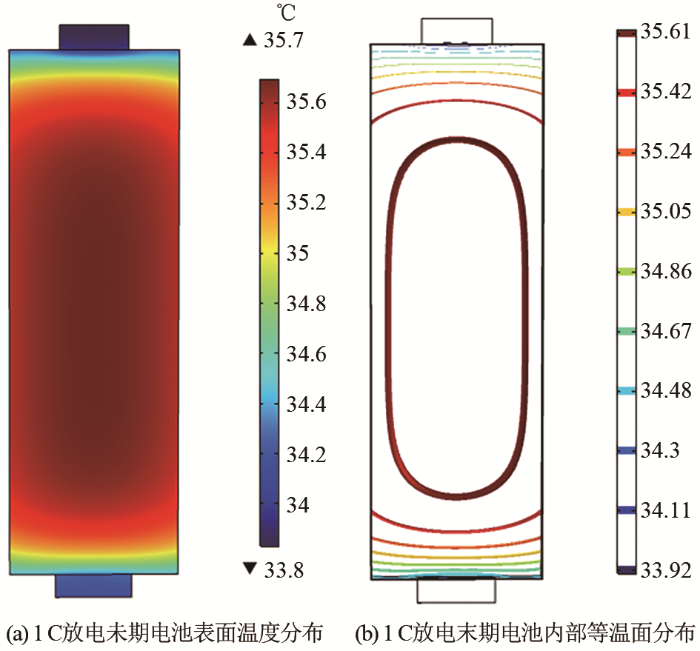
从图7(a)～(c)可知，平均温升随着正极厚度的增加而增加，这是由于正极厚度增加使得厚度方向的锂离子浓度梯度增大，导致极化内阻增加，不可逆热增大，最终电池温度增加。等高线密度随着正极厚度增加而增加，温升趋势增快。正极厚度低到一定程度以后对温升的影响就不明显了，反而会影响电池容量，因此正极厚度不宜过低。极板宽度和负极极耳宽的增加能略微减缓温升的增加程度。这是由于极板和负极的热导率较大，宽度增加以后电池的横截面积增大，电池中心热量更容易传向电池两侧，提高了降温能力。图7(d)表明正极极耳厚度与负极极耳宽度交互时，温升几乎不会沿着正极极耳厚度方向增加。

根据图8(b)可知，正极厚度在50～70 μm时，随着负极极耳宽的增加，电池温差先减小后增加，最小值出现在70～80 mm。这可能是由于负极极耳宽度的增加引起其产热密度减小，它的值逐渐先靠近而后又远离电芯的产热密度，导致与电芯的换热量先减小后增加。图8(a)表明温差最小值出现于正极极耳厚度0.6～0.7 mm的区间。如图8(c)所示极耳的厚度与宽度对电池温差的影响都不是单调的，在一定区间内存在最小值。

图9为放电末期实验电池的表面温度分布和内部等温面分布。根据有限元模型的结果，电池的最大温度和最大温差均在放电末期，最大温度点处在电池中心偏向正极侧（图中下侧）。温度最低点出现在极耳端，因此显然能判断出极耳尺寸直接影响最低温度点的数值和分布，所以在合理范围内调节负极极耳的尺寸能够改善电池的热均匀性。

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 电池放电末期温度分布

Fig.9 Temperature distribution at end of battery discharge

2.3　优化结果

将SGD极值所得的最优解参数输入到电化学-热耦合模型里验证优化后的效果，优化前后与圆整后的结果见表5。优化以后的平均温升为6.452 ℃，最大温差为1.126 ℃，与验证值误差均不超过2.68%，由此证明了模型优化的精确性。考虑加工制造成本，将设计参数取圆整值，平均温升比优化前降低了2.93 ℃，最大温差降低了0.596 ℃。电池的均温性和温升得到了较大改善，达到了产品多目标优化的目的。

表5 优化结果对比

Table 5 Comparison of optimization results

项目	L_pos/μm	W_p/cm	TH_pos/mm	W_pos/mm	TH_neg/mm	W_neg/mm	T_ave/℃	ΔT_max/℃
优化前	90	10.95	0.3	50	0.2	45	9.49	1.771
优化后	50.521	33.203	0.653	58.352	0.694	73.009	6.452	1.126
验证值	50.521	33.203	0.653	58.352	0.694	73.009	6.53	1.157
圆整值	51	33	0.7	58	0.7	73	6.56	1.175

新窗口打开| 下载CSV

3 结论

通过将电极对与单体电池耦合，提出了一种便捷计算的三维电化学-热耦合模型，利用响应面法，线性加权组合法和随机梯度下降法分析正极厚度，极板尺寸和正负极耳尺寸对电池温度的影响，主要结论为：①通过耦合电极对与单体电池建立三维有限元模型能够准确分析电池温度场；②正极厚度与平均温升正相关，但是厚度低到一定程度以后对其影响就不明显了，极板宽度、极耳宽度和极耳厚度的增加能够降低电池温升，但是超过一定范围时会降低电池的均温性；③经优化以后，电池的平均温升降低2.93 ℃，最大温差降低0.596 ℃，方案误差小于2.68%。电池的最大温升为6.56 ℃，比优化前降低了30.9%；最大温差为1.175 ℃，比优化前降低了33.7%。本文建立的多目标优化方法可用于其他电池的设计参数优化，在指导锂离子电池单体结构设计上具有良好的参考意义。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

ARAI

, YAMAKI

, YAMAUCHI

, et al.

Development of a high power lithium secondary battery for hybrid electric vehicles

[J]. Journal of Power Sources, 2005, 146(1): 788-792.