图3
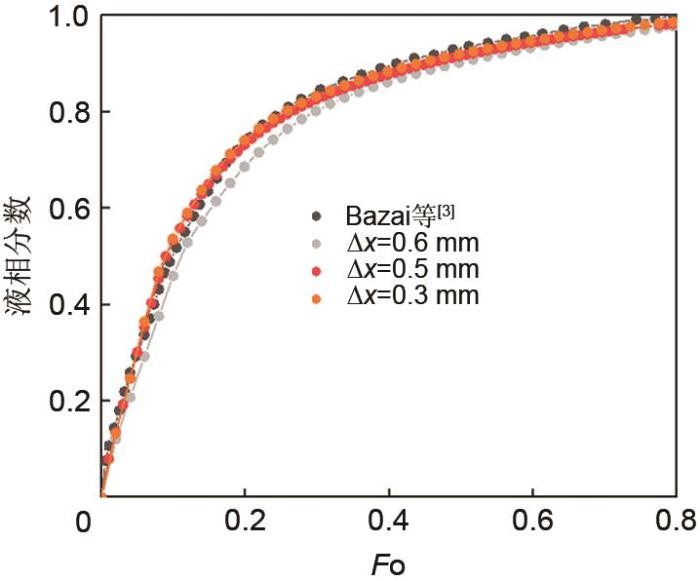
网格无关性验证
Fig. 3
Grid independence verification
图4
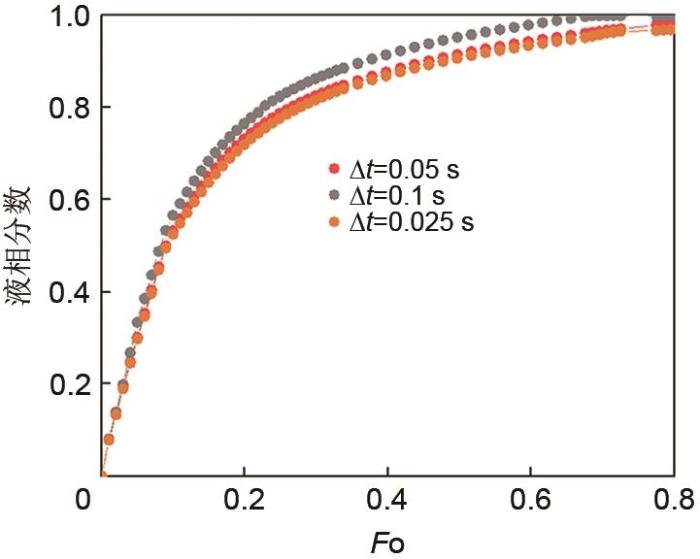
时间步长无关性验证
Fig. 4
Time step independence verification
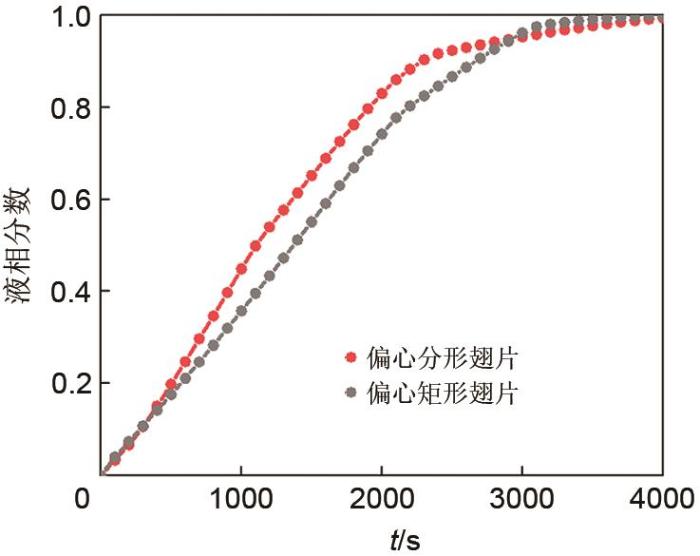
图5
熔化分数对比
Fig. 5
Correlation of melting fraction
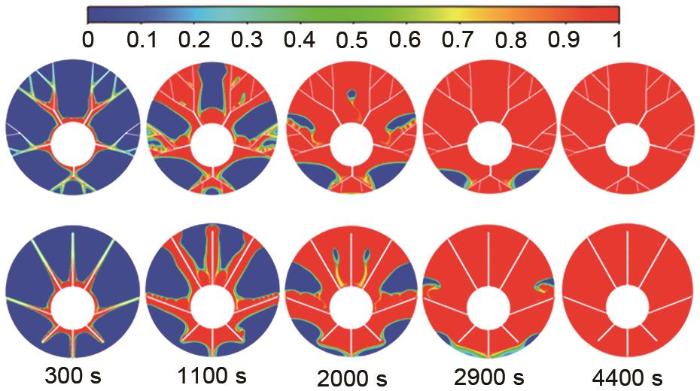
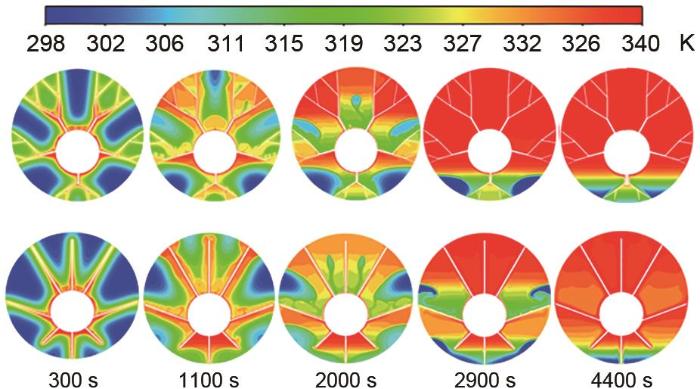
图6
熔化分数云图
Fig. 6
Fusion fraction cloud image
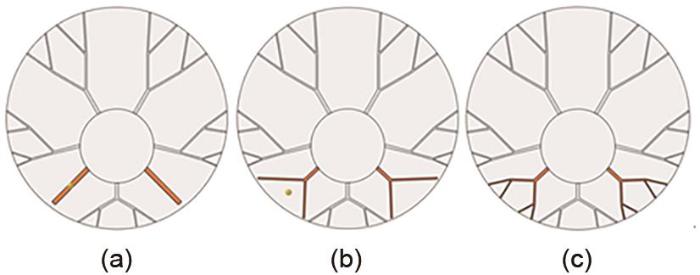
图8
局部强化结构
Fig. 8
Locally strengthened structure
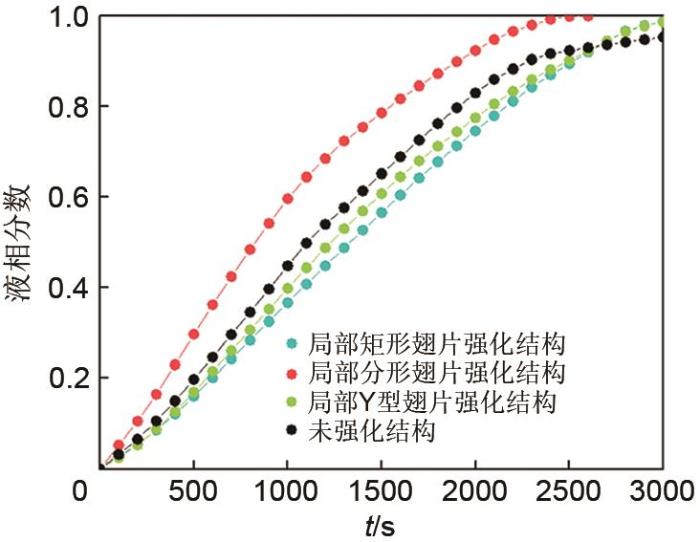
图9
液相分数对比
Fig. 9
Liquid fraction correlation
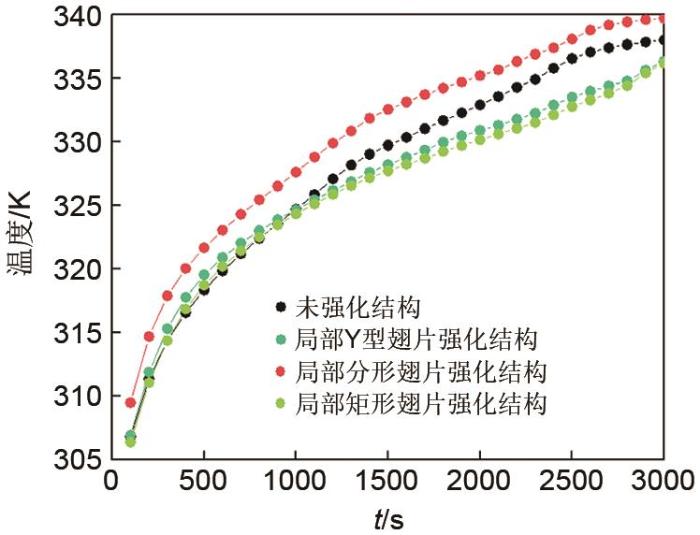
图10
液相温度对比
Fig. 10
Liquid phase temperature correlation
[1]
吴学红, 翟亚妨, 姜文涛, 等. 套管式相变蓄热器强化传热研究[J]. 可再生能源, 2016, 34(7): 983-989.
[本文引用: 1]
WU X H, ZHAI Y F, JIANG W T, et al. Heat transfer enhancement for sleeve thermal energy storage exchanger using phase change materials[J]. Renewable Energy Resources, 2016, 34(7): 983-989.
[本文引用: 1]
[2]
顾煜炯, 张晨, 耿直, 等. 新型套管式相变蓄热器结构优化及传热研究[J]. 热力发电, 2018, 47(1): 33-37.
[本文引用: 1]
GU Y J, ZHANG C, GENG Z, et al. Structure optimization and heat transfer research for new type casing phase change heat sequencer[J]. Thermal Power Generation, 2018, 47(1): 33-37.
[本文引用: 1]
[3]
BAZAI H, MOGHIMI M A, MOHAMMED H I, et al. Numerical study of circular-elliptical double-pipe thermal energy storage systems[J]. Journal of Energy Storage, 2020, 30: doi: 10.1016/j.est.2020.101440.
[本文引用: 2]
[4]
SAFARI V, ABOLGHASEMI H, DARVISHVAND L, et al. Thermal performance investigation of concentric and eccentric shell and tube heat exchangers with different fin configurations containing phase change material[J]. Journal of Energy Storage, 2021, 37: doi: 10.1016/j.est.2021.102458.
[本文引用: 1]
[5]
ALNAKEEB M A, ABDEL SALAM M A, HASSAB M A. Eccentricity optimization of an inner flat-tube double-pipe latent-heat thermal energy storage unit[J]. Case Studies in Thermal Engineering, 2021, 25: doi: 10.1016/j.csite.2021.100969.
[本文引用: 1]
[6]
PAHAMLI Y, HOSSEINI M J, RANJBAR A A, et al. Analysis of the effect of eccentricity and operational parameters in PCM-filled single-pass shell and tube heat exchangers[J]. Renewable Energy, 2016, 97: 344-357.
[本文引用: 1]
[7]
CAO X L, YUAN Y P, XIANG B, et al. Effect of natural convection on melting performance of eccentric horizontal shell and tube latent heat storage unit[J]. Sustainable Cities and Society, 2018, 38: 571-581.
[本文引用: 1]
[8]
YAZICI M Y, AVCI M, AYDIN O, et al. On the effect of eccentricity of a horizontal tube-in-shell storage unit on solidification of a PCM[J]. Applied Thermal Engineering, 2014, 64(1/2): 1-9.
[本文引用: 1]
[9]
KADIVAR M R, MOGHIMI M A, SAPIN P, et al. Annulus eccentricity optimisation of a phase-change material (PCM) horizontal double-pipe thermal energy store[J]. Journal of Energy Storage, 2019, 26: doi: 10.1016/j.est.2019.101030.
[本文引用: 1]
[10]
DARZI A R, FARHADI M, SEDIGHI K. Numerical study of melting inside concentric and eccentric horizontal annulus[J]. Applied Mathematical Modelling, 2012, 36(9): 4080-4086.
[本文引用: 1]
[11]
YAGCI O K, AVCI M, AYDIN O. Melting and solidification of PCM in a tube-in-shell unit: Effect of fin edge lengths' ratio[J]. Journal of Energy Storage, 2019, 24: doi: 10.1016/j.est.2019.100802.
[本文引用: 1]
[12]
KUMAR R, VERMA P. An experimental and numerical study on effect of longitudinal finned tube eccentric configuration on melting behaviour of lauric acid in a horizontal tube-in-shell storage unit[J]. Journal of Energy Storage, 2020, 30: doi: 10.1016/j.est.2020.101396.
[本文引用: 1]
[13]
MAHDI J M, LOHRASBI S, GANJI D D, et al. Accelerated melting of PCM in energy storage systems via novel configuration of fins in the triplex-tube heat exchanger[J]. International Journal of Heat and Mass Transfer, 2018, 124: 663-676.
[本文引用: 1]
[14]
夏天亮. 套管式相变储能单元肋片强化传热研究[D]. 扬州: 扬州大学, 2021.
[本文引用: 1]
XIA T L. Research of heat transfer enhancement by fins in the tube-and-tube phase change energy storage unit[D]. Yangzhou: Yangzhou University, 2021.
[本文引用: 1]
[15]
ZHANG S Q, PU L, XU L L, et al. Melting performance analysis of phase change materials in different finned thermal energy storage[J]. Applied Thermal Engineering, 2020, 176: 15425.
[本文引用: 1]
[16]
HOSSEINI M J, RANJBAR A A, RAHIMI M, et al. Experimental and numerical evaluation of longitudinally finned latent heat thermal storage systems[J]. Energy and Buildings, 2015, 99: 263-272.
[本文引用: 1]
[17]
朱玉熙. 翅片管相变储热系统数值模拟及结构优化[D]. 济南: 山东大学, 2021.
[本文引用: 1]
ZHU Y X. Numerical simulation and structural optimization of latent heat storage system with fins[D]. Jinan: Shandong University, 2021.
[本文引用: 1]
[18]
PU L, ZHANG S Q, XU L L, et al. Thermal performance optimization and evaluation of a radial finned shell-and-tube latent heat thermal energy storage unit[J]. Applied Thermal Engineering, 2020, 166: doi: 10.1016/j.applthermaleng.2019.114753.
[本文引用: 1]
[19]
ZHANG C B, LI J, CHEN Y P. Improving the energy discharging performance of a latent heat storage (LHS) unit using fractal-tree-shaped fins[J]. Applied Energy, 2020, 259: doi: 10.1016/j.apenergy.2019.114102.
[本文引用: 1]
[20]
SHEIKHOLESLAMI M, LOHRASBI S, GANJI D D. Numerical analysis of discharging process acceleration in LHTESS by immersing innovative fin configuration using finite element method[J]. Applied Thermal Engineering, 2016, 107: 154-166.
[本文引用: 1]
[21]
李杰. 树状肋储能换热器的固液相变传热特性研究及其结构优化[D]. 南京: 东南大学, 2019.
[本文引用: 1]
LI J. Study on the solid-liquid phase change heat transfer characteristics in thermal energy storage heat exchanger with tree-shaped fin and its structural optimization[D]. Nanjing: Southeast University, 2019.
[本文引用: 1]
[22]
SCIACOVELLI A, GAGLIARDI F, VERDA V. Maximization of performance of a PCM latent heat storage system with innovative fins[J]. Applied Energy, 2015, 137: 707-715.
[本文引用: 1]
[23]
柯彬彬. 圆管外石蜡相变传热过程数值模拟及传热强化[D]. 镇江: 江苏大学, 2016.
[本文引用: 1]
KE B B. Numerical simulation and heat transfer enhancement of paraffin phase change heat transefer process at outer tube[D]. Zhenjiang: Jiangsu University, 2016.
[本文引用: 1]
[24]
RABIENATAJ DARZI A A, JOURABIAN M, FARHADI M. Melting and solidification of PCM enhanced by radial conductive fins and nanoparticles in cylindrical annulus[J]. Energy Conversion and Management, 2016, 118: 253-263.
[本文引用: 1]
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
2
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
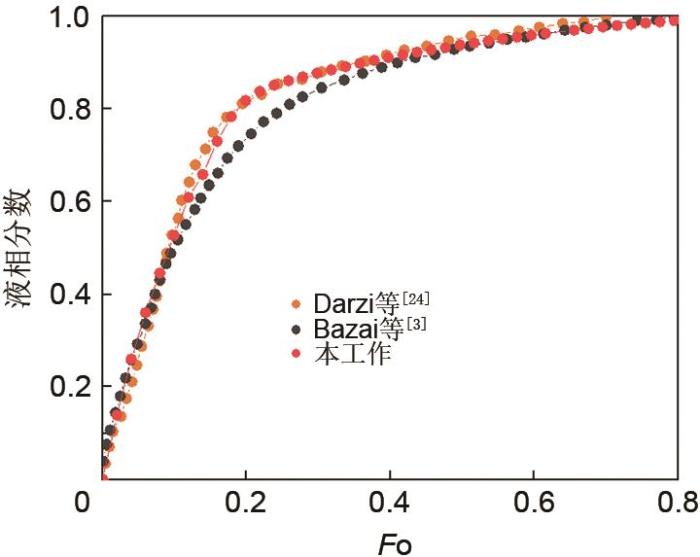
... 为了验证所得到的结果,用Darzi等[24 ] 和Bazai等[3 ] 的研究来对本工作所用模型进行验证,如图2 所示.文献所用的相变材料为正二十烷,其物性参数见表4 .其边界条件为内管壁T w =329.15 K,外管壁q =0,PCM初始温度为T pre =308.15 K. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 吴学红等[1 ] 对相变材料的融化凝固性能进行了实验研究,发现供热管道间翅片和斜翅片的添加改善了蓄热器内部的温度分层,缩短了温度达到均匀化的时间.顾煜炯等[2 ] 对换热器的管束应用不同的排布方式,数值模拟后发现同心圆排列所需的融化时间最短.Bazai等[3 ] 用数值模拟研究了内管直径在不同长宽比下以及内椭圆管在不同角度下的熔化凝固过程,结果显示融化过程中最佳纵横比是⅓H ,最佳角度是90°,凝固过程纵横比影响不显著.Safari等[4 ] 通过实验和数值模拟的方式研究了矩形翅片和分形翅片在不同排列以及组合方式下石蜡完全融化时间的变化.Alnakeeb等[5 ] 用数值模拟对内扁平管双管潜热储存单元在不同长宽比下不同的偏心率对PCM总熔化时间的影响做了研究.Pahamli等[6 ] 得出增大偏心率会提高熔化结束阶段的传热速率和平均温度.Cao等[7 ] 采用实验研究与数值模拟相结合的方法分析了随着Ra 的增加,不同偏心率下壳管潜热蓄热装置的时间平均传热系数的变化.Yazici等[8 ] 通过对石蜡的凝固过程进行实验研究得出随着偏心率增加,无论内管向上还是向下偏移,均会使凝固时间增加.Kadivar等[9 ] 对内管进行了径向和轴向偏心,用数值模拟分析了偏心比对熔化特性的影响,用响应面得出了最佳偏心几何形状,使熔化时间快了7倍.Darzi等[10 ] 发现在15 min前,同心和偏心熔化速率大致相同,之后同心熔化速率降低,这是由于自然对流的出现.Yagci等[11 ] 用实验方法得出减小翅片的上下长度比后,熔化时间缩短,凝固时间基本不受影响.Kumar等[12 ] 用数值模拟和实验研究分析了储存单元底部环空翅片夹角为60°、120°和180°时,在不同偏心位置的环形内PCM的熔化速率.Mahdi等[13 ] 用数值模拟计算得出使用不均匀翅片可以充分提高三管储能系统中相变材料熔化速率.夏天亮[14 ] 设计了一种内管带Y形肋的套管式相变储能单元,缩短了相变材料蓄放热时间.Zhang等[15 ] 采用双螺旋和四螺旋翅片提高了蓄热单元的热性能.Hosseini等[16 ] 用数值模拟和实验研究了翅片高度和Stefan对双管热交换器中相变材料充电性能的影响,结果表明Stefan的增加会使熔化速率加快且在低Stefan下增大翅片高度比高Stefan下更有效.朱玉熙[17 ] 提出非等径和非等距环形翅片布置,结果表明,两种优化方法显著改善了融化过程的传热.Pu等[18 ] 通过数值模拟对环形翅片的排列方式进行了探索,结果表明算术翅片的熔化时间最短,上翅片的熔化时间最长.Zhang等[19 ] 用数值模拟对树状翅片与矩形翅片的充放电性能进行了比较,得出树翅装置减少了完全凝固时间.Sheikholeslami等[20 ] 从放电性能和最大储能两个角度比较了PCM中纳米颗粒分散和添加不同结构的翅片对LHTESS性能的影响.结果表明雪花翅片的放电过程强化效果较纳米颗粒分散强,但并没有减少最大储能容量.李杰[21 ] 通过对树状肋储能换热器的凝固过程进行模拟发现,其释放能速率提高主要在中后期.Sciacovelli等[22 ] 将Y形分支翅片改进为双Y形分支,使放电效率增加了约24%. ...
1
... 物理模型如图1 所示,热流体管道的内管直径D 1 为50 mm,外管直径D 0 为150 mm,管材均为铝.图1 (a)为偏心矩形翅片储能单元模型,其结构参数见表1 ,其中L 1 代表顶部翅片长度,其余依次按逆时针排序为L 2 ~L 5 ;(b)为偏心分形翅片储能单元模型,其一级分支夹角60°,二级分支夹角30°,内管偏心率均为0.4[E =e (偏心距)/(R 0 -R 1 )],其结构参数见表2 ,其中L 10 代表顶部主干翅片长度,L 11 代表顶部一分支翅片长度,L 12 代表顶部二分支翅片长度,其余依次按逆时针排序为L 2 ~L 3 ,W 0 ~W 2 分别为主干、一分支和二分支翅片宽度.选择石蜡为蓄热材料,其热物性参数[23 ] 见表3 . ...
1
... 物理模型如图1 所示,热流体管道的内管直径D 1 为50 mm,外管直径D 0 为150 mm,管材均为铝.图1 (a)为偏心矩形翅片储能单元模型,其结构参数见表1 ,其中L 1 代表顶部翅片长度,其余依次按逆时针排序为L 2 ~L 5 ;(b)为偏心分形翅片储能单元模型,其一级分支夹角60°,二级分支夹角30°,内管偏心率均为0.4[E =e (偏心距)/(R 0 -R 1 )],其结构参数见表2 ,其中L 10 代表顶部主干翅片长度,L 11 代表顶部一分支翅片长度,L 12 代表顶部二分支翅片长度,其余依次按逆时针排序为L 2 ~L 3 ,W 0 ~W 2 分别为主干、一分支和二分支翅片宽度.选择石蜡为蓄热材料,其热物性参数[23 ] 见表3 . ...
1
... 为了验证所得到的结果,用Darzi等[24 ] 和Bazai等[3 ] 的研究来对本工作所用模型进行验证,如图2 所示.文献所用的相变材料为正二十烷,其物性参数见表4 .其边界条件为内管壁T w =329.15 K,外管壁q =0,PCM初始温度为T pre =308.15 K. ...