高能量密度锂离子电池老化半经验模型

doi:10.19799/j.cnki.2095-4239.2021.0725

高能量密度锂离子电池老化半经验模型

祝庆伟^,¹, 俞小莉², 吴启超², 徐一丹², 陈芬放², 黄瑞^,²

1.浙江大学工程师学院，浙江杭州 310015

2.浙江大学能源工程学院，浙江杭州 310027

Semi-empirical degradation model of lithium-ion battery with high energy density

ZHU Qingwei^,¹, YU Xiaoli², WU Qichao², XU Yidan², CHEN Fenfang², HUANG Rui^,²

1.Polytechnic Institute, Zhejiang University, Hangzhou 310015, Zhejiang, China

2.College of Energy Engineering, Zhejiang University, Hangzhou 310027, Zhejiang, China

通讯作者: 黄瑞，高级实验师，研究方向为汽车及动力机械实验教学、汽车及动力机械试验技术，E-mail：hrss@zju.edu.cn。

收稿日期: 2021-12-31 修回日期: 2022-01-13

基金资助:

浙江省自然科学基金项目. LQ20E060008
浙江大学实验技术研究项目. SYB202109

Received: 2021-12-31 Revised: 2022-01-13

作者简介 About authors

祝庆伟（1998—），男，硕士研究生，研究方向为电池老化与热管理，E-mail：qwzhu@zju.edu.cn； E-mail：qwzhu@zju.edu.cn。

摘要

电池循环老化过程中容量会不断衰退，内阻也会逐渐增长，从而影响电池的使用寿命与性能表现。为建立电池容量衰退与内阻增长半经验模型，缩短探究电池老化特性所需的实验时间，采用具有高能量密度的21700锂离子电池，在0 ℃、23 ℃和40 ℃条件下结合1 C和2 C两种放电倍率组成了六种工况，对电池进行循环老化实验，分析温度等因素对电池容量衰退与内阻增长特性的影响规律。在结合Arrhenius方程建立电池容量衰退半经验模型时，额外引入了两个关于循环次数的幂函数和常数项，拓展了容量衰退半经验模型的适用性，使其能够适用于不同温度下表现出的不同容量衰减趋势。采用双指数函数累乘的公式形式建立了电池内阻增长的半经验模型，能够有效地预测内阻在不同工况下的增长规律。并利用交叉验证的方法证明了容量衰退与内阻增长半经验模型的准确性，能够用于预测电池在其他温度条件下的老化规律。最后利用建立的电池老化半经验模型，预测了该电池在15 ℃、30 ℃和45 ℃的容量与内阻变化情况，有助于更全面地了解电池的老化特性，并避免了大量重复实验，有利于提高研究效率。

关键词： 锂离子电池 ; 容量衰退 ; 内阻增长 ; 老化半经验模型

Abstract

The capacity of the battery will continue to fall as the cycle ages, and the internal resistance will progressively grow, affecting the battery's service life and performance. To establish the semi-empirical model of capacity decline and internal resistance growth and shorten the time required to investigate the battery aging characteristics, the 21700 lithium-ion battery with high energy density is adopted to conduct the cycle aging experiment of the battery under six working conditions at 0 ℃, 23 ℃, and 40 ℃ combined with 1 C and 2 C discharge rates. The effect of temperature and other environmental conditions on battery capacity reduction and internal resistance increase is investigated.When the semi-empirical model of battery capacity decline is created by combining the Arrhenius equation, an additional power function and a constant term about the number of cycles are introduced, which can broaden the model's applicability and make it suitable for different capacity decline trends at different temperatures. A semi-empirical model of battery internal resistance growth is developed using the double exponential function multiplication formula, which can effectively predict the law of internal resistance growth under various working conditions. The cross-validation approach is used to demonstrate the accuracy of semi-empirical models of capacity decrease and internal resistance increase, which may be used to forecast the aging law of batteries at various temperatures. Finally, the semi-empirical model of battery aging is used to predict the capacity and internal resistance of the battery at 15 ℃, 30 ℃, and 45 ℃, allowing for a better understanding of the battery's aging characteristics while avoiding a large number of repeated experiments and increasing research efficiency.

Keywords： lithium-ion battery ; capacity decline ; internal resistance growth ; semi-empirical degradation model

PDF (2078KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

祝庆伟, 俞小莉, 吴启超, 徐一丹, 陈芬放, 黄瑞. 高能量密度锂离子电池老化半经验模型[J]. 储能科学与技术, 2022, 11(7): 2324-2331

ZHU Qingwei. Semi-empirical degradation model of lithium-ion battery with high energy density[J]. Energy Storage Science and Technology, 2022, 11(7): 2324-2331

近年来，新能源汽车产销量不断增加，而锂离子电池因具有绿色环保、能量密度高、无记忆效应以及自放电率低等优点成为了新能源汽车动力电池的首选。随着使用时间的不断累积，锂电池会不断地老化，表现为可用容量的逐渐衰减与内阻的不断增加^[1]。一般当电池的容量衰退20%，或内阻增加一倍后就不再使用该电池^[2]，因此需要在使用过程中对电池的健康状态进行预测^[3]。同时电池的内阻增长会导致电池在使用时产生更多的热量，严重时甚至会引发热失控。因此这两个性能参数与电池的使用寿命和安全性关系密切，对电池的老化研究至关重要。

目前的研究集中在不同的使用条件对电池老化性能的影响规律，并建立电池老化预测模型，从而进一步指导电池的实际使用。常考虑的老化影响因素有温度、充放电倍率、充放电截止电压等，在建立电池老化半经验模型时常采用Arrhenius公式、逆幂律公式和双指数公式等。

Waldmann等^[4]采用NCM/LMO混合正极电池在较大的温度范围内做了电池老化实验，发现除25 ℃以外，容量均近似线性衰减。Wang等^[5]考虑到LFP电池在不同DOD下循环时放电量的不同，结合Arrhenius公式，建立了容量与温度、倍率以及安时吞吐量的半经验模型。Li等^[6]除了关注温度与倍率外，还考虑了截止电压对LFP电池容量与内阻的影响，同时探究了双因素组合对电池老化的耦合作用，并结合Arrhenius公式与逆幂律公式建立多因素耦合的寿命预测模型。Lewerenz等^[7]研究发现LFP电池的容量衰退与内阻增长之间具有相关性，当容量偏离线性衰退时内阻快速增加。Guan等^[8]在30% DOD的实验条件下进行研究，发现循环倍率对LCO电池容量衰退的影响存在一个临界值，大于或小于该倍率都不会加深电池的老化。此外，Gao等^[9]发现对于LCO电池的老化过程，充电截止电压也存在一个临界值，当超过该临界值时容量与内阻变化剧烈，并据此建立了容量衰退关于充电电流与充电截止电压的半经验模型。张金等^[10]在双指数模型的基础上推导出更加简单的三参数容量衰退模型，提高了预测LCO电池老化程度的鲁棒性与实用性。刘建等^[11]建立的LCO电池容量衰退半经验模型不仅考虑了温度和循环倍率，还考虑了充电截止电压。

更高的能量密度是电池的发展方向之一，但目前已有的研究多采用LCO电池、LFP电池或LMO电池，对于具有高能量密度的NCA电池研究较少，而通过实验发现NCA电池的老化特性与其他类型的电池存在差异，并不适用于现有的容量衰退半经验模型。此外，目前的研究只针对电池的容量衰退进行建模，没有考虑内阻的增长，但内阻关系着电池的产热，影响电池的使用，因此还需要建立有效的模型对内阻进行预测。然而，为了得到电池在不同工况下的老化规律，需消耗大量的时间对电池进行老化实验。

针对以上存在的问题，本文以具有高能量密度的21700电池为研究对象，通过实验探究电池在不同使用工况下的老化特性，并据此建立预测电池容量衰退与内阻增长的半经验模型，最后通过该模型对电池在其他温度条件下的老化规律进行预测，有利于更全面地认识电池的老化特性以及缩短探究电池老化规律所需的实验时间。

1 实验方案设计

1.1　研究对象与实验平台

采用由SAMSUNG SDI公司生产的21700-50E电池作为研究对象，该电池为具有较高能量密度的NCA电池，符合电池的发展方向，其主要性能参数如表1所示。

表1 21700-50E电池主要性能参数

Table 1 Main performance parameters of 21700-50E battery

参数	数值
能量密度/(Wh/kg)	260.9
重量/g	69.5
额定容量/Ah	4.9
额定电压/V	3.63
最大充电电流/A	4.9
最大持续放电电流/A	9.8
充电截止电压/V	4.2
放电截止电压/V	2.5
循环充放电温度范围/℃	0～45

新窗口打开| 下载CSV

电池老化实验与基本性能测试实验平台如图1所示，主要由上位机、恒温箱和电池充放电测试设备组成，电池在实验时放置在恒温箱中。恒温箱型号为ESPEC GPU-3，其温度测量范围为-40～180 ℃，温度波动范围在0.5 ℃以内，温度均匀度在2 ℃以内。电池充放电测试设备型号为Neware CT4008-5V12A，电流与电压的测试精度为满量程的0.05%，记录频率为10 Hz。

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 实验平台

Fig. 1 The experiment platform

1.2　电池实验设计

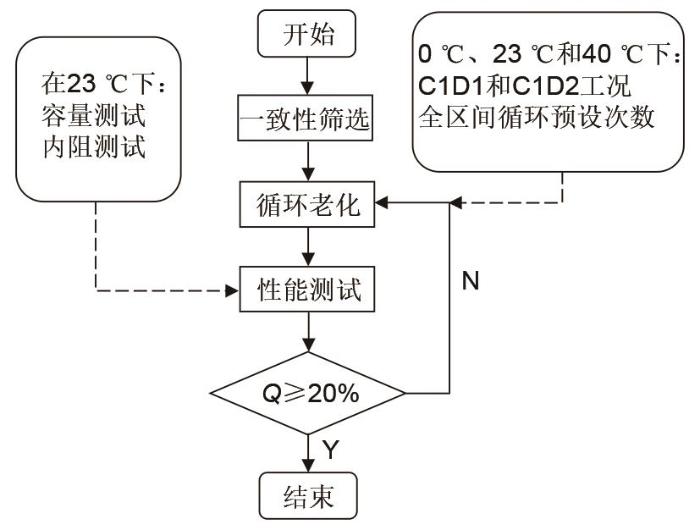
实验分为循环老化实验与基本性能测试实验两部分，总的实验流程如图2所示。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 实验流程图

Fig. 2 Experimental flow chart

在循环实验开始之前，对电池进行一致性筛选，选取18节初始容量差异在1%以内的电池，并分为6组进行后续实验。

循环老化实验中选择0 ℃、23 ℃和40 ℃三个温度水平，放电倍率选取1 C和2 C两个水平，由于电池老化实验工作量大，为缩短实验时间，充电倍率始终为1 C，循环区间为[0,100%]。充电阶段为恒流恒压充电，截止电压为4.2 V，截止电流为98 mA；放电阶段为恒流放电，截止电压为2.5 V。每经过一定的循环次数后进行一次基本性能测试，直到容量衰退到初始容量的80%以后结束实验。

性能测试分为容量测试和内阻测试两部分，为了使性能测试结果具有可比性，所有的性能测试都在23 ℃环境下进行，并且每个工况下容量与内阻的值都取3节电池的平均值作为最终测试结果。容量测试时首先按照2.45 A和4.2 V进行恒流恒压充电，截止电流为98 mA，搁置30 min后以1 C放电至2.5 V，并搁置30 min。重复以上步骤3次，取最后一次容量测试结果为当前可用容量。内阻测试采用HPPC测试方法，电池在SOC为20%～80%的常用范围内变化不大，在较低和较高的SOC范围内由于极化的影响内阻会显著变大，本文测试50% SOC处的内阻作为当前状态下的内阻。

2 容量衰退实验结果分析

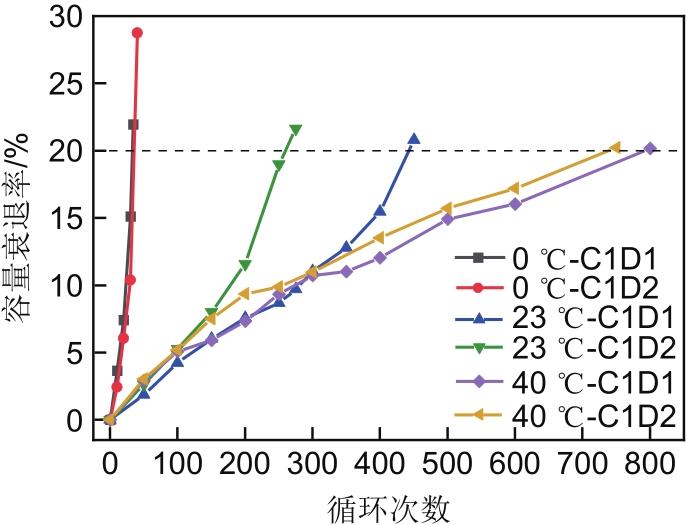
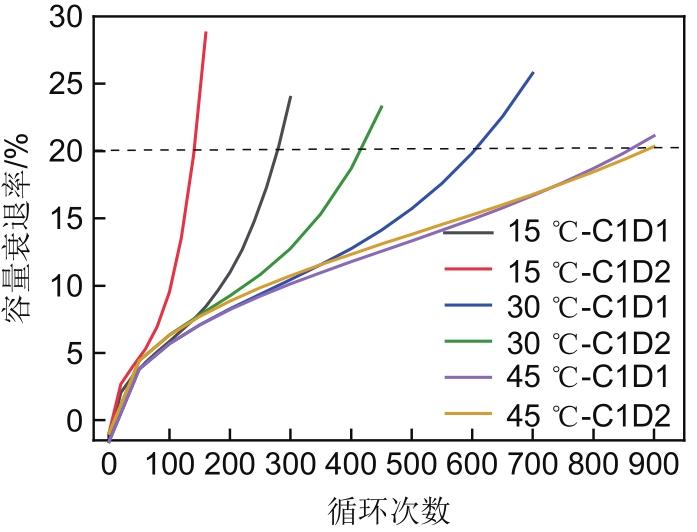
图3为电池在不同工况下的容量衰退测试结果，其中0 ℃-C1D2的含义为：循环时温度为0 ℃，按照1 C充电和2 C放电，其他工况类似。

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 电池容量衰退测试结果

Fig. 3 Battery capacity decline test results

2.1　影响电池容量衰退的因素

从图3可以看出随着温度的增加，电池容量衰退20%所需的循环次数越来越多，在0 ℃和40 ℃下循环时，C1D1和C1D2工况下的老化曲线很接近，而在23 ℃下循环时，两种工况下的老化曲线相差较大；当电池在23 ℃和40 ℃循环时，C1D2工况的曲线始终在C1D1工况曲线的上方，说明此时大倍率放电会加快电池老化，而电池在0 ℃循环时则相反，因此该电池在不同放电倍率下的老化规律受电池循环温度的影响；电池在0 ℃和23 ℃循环时，老化曲线的斜率随着循环次数的增加呈变大的趋势，电池老化速率逐渐加快，而在40 ℃下循环时则相反，因此温度是影响该电池老化最主要的因素。

2.2　建立容量衰退半经验模型

为了对电池在循环使用过程中的容量进行实时预测，目前常用的有两种方法，第一种是建立电化学模型，可以反映电池内部反应机理，准确性较高，但是模型较为复杂；第二种方式为根据实验数据建立半经验模型，计算量较小，能够适用于一般的使用场景，因此本文采用半经验模型方法进行建模。

2.2.1　结合温度与循环次数建立容量衰退模型

当前的研究常结合如式(1)的Arrhenius方程建立电池容量衰退半经验模型，即将温度对电池容量的影响拟合成一个指数函数，并将温度放置于指数上，如式(2)。从图3可以发现电池的容量衰退率在前期较为线性，主要是由于在这段过程中电池内部SEI膜逐渐形成，电池内部化学体系比较稳定。随着老化程度的不断加深，电池内部结构逐渐破坏，其老化速度发生改变。因此循环次数对电池容量衰退率的影响通常被拟合成一个如式(3)的幂函数，从而体现出随着老化时间增加容量衰退的变化，并将其与式(2)相乘，建立耦合温度与循环次数的半经验模型，如式(4)所示。

Q_{1} = A \times e^{- \frac{E_{a}}{R * T}}

(1)

Q_{2} = B \times e^{f (T)}

(2)

Q_{3} = n^{C}

(3)

Q_{4} = D \times e^{f (T)} \times n^{E}

(4)

式中：Q₁、Q₂、Q₃和Q₄为容量衰退率，A为指前因子，E_a为活化能，R为气体常数，T为温度，B、C、D和E为待拟合参数，n为循环次数。

在MATLAB的Curve Fitting Tool工具箱中参照式(4)编写自定义公式进行曲线拟合，得到的拟合结果如图4所示。

图4

新窗口打开| 下载原图ZIP| 生成PPT

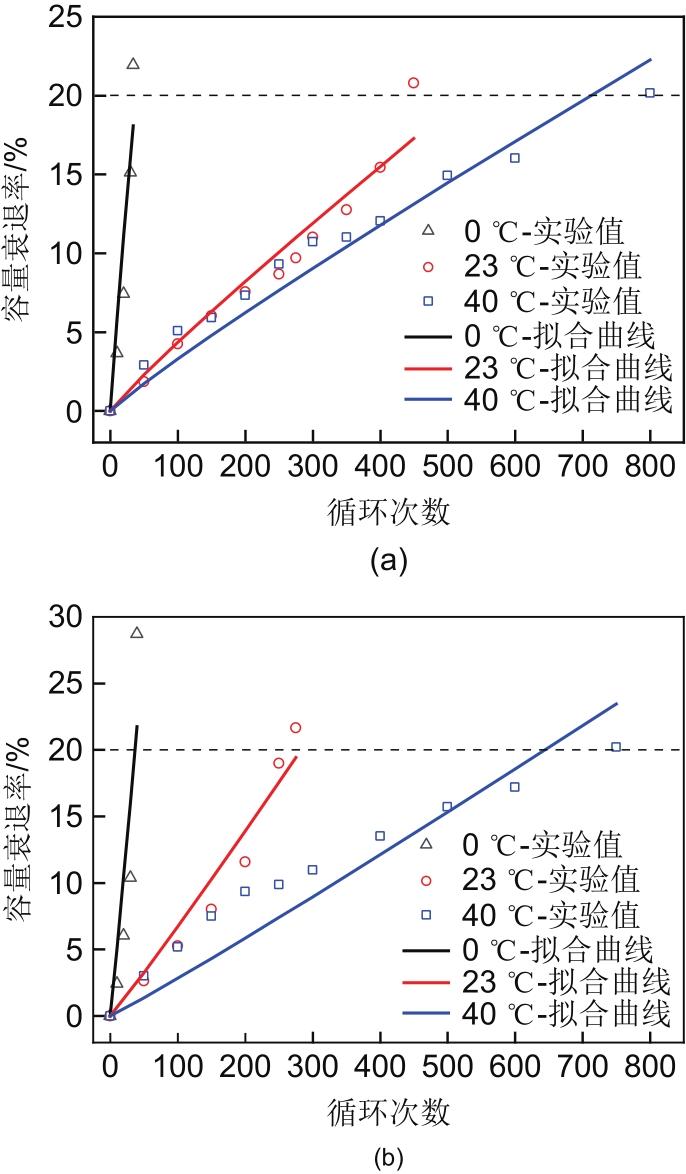
图4 参照式(4)的拟合结果(a) C1D1工况(b) C1D2工况

Fig. 4 Fitting result of reference formula (4) (a) C1D1 condition (b) C1D2 condition

从图4中可以看出由于在不同温度下表现出了不同的容量衰减趋势，拟合曲线并没有很好地符合实际情况，主要是由于在当前研究中，电池的容量衰退速率大多随着循环次数的累计而逐渐增大，容量衰退率曲线逐渐上翘，即式(3)中的参数C大于1，而本研究中，电池在0 ℃和23 ℃下循环老化时曲线呈现上翘趋势，而在40 ℃循环老化时，老化曲线逐渐下弯，即参数C小于1，然而从式(5)中可以看出参数E决定了容量衰退率关于循环次数n的曲线凹凸性，因此仅靠式(4)的形式则无法体现出这种不同的老化趋势的变化。因此在式(4)的基础上额外引入两个幂函数和常数项，用于表现容量衰退速率在不同温度下的差异，公式模型如式(6)所示，并由式(7)可知此时容量衰退率Q关于循环次数n的曲线凹凸性还受到参数I的影响，因此可以通过选取适当的参数优化曲线的凹凸性，从而能够适用于在不同工况下具有不同曲线变化规律时的情况。

\frac{\partial Q_{4}}{\partial n} = D E e^{f (T)} n^{E - 1}

(5)

Q = D e^{F + \frac{G}{T + H}} n^{E} + n^{I} + J

(6)

\frac{\partial Q}{\partial n} = D E e^{F + \frac{G}{T + H}} n^{E - 1} + I n^{I - 1}

(7)

式中，Q为容量衰退率，F、G、H、I和J为待拟合参数。

（1）C1D1工况下的拟合

根据式(6)对C1D1工况下的实验数据在MATLAB的工具箱中进行拟合，结果如式(8)所示。

Q_{C 1 D 1} = 0.0119 e^{- 27.78 + \frac{432}{T + 20.38}} n^{3.968} + n^{0.4305} - 1.576

(8)

式中，Q_C1D1为电池在C1D1工况下的容量衰退率预测值。

在统计学中，R-square和RMSE是用来衡量拟合数据与实际真值之间拟合优度的参数，R-square的范围是[0,1]，其值越大拟合效果越好，RMSE是均方根误差，其值越小拟合效果越好。在C1D1工况下拟合的结果式(8)的R-square为0.9600，RMSE为1.3229，表明拟合结果与实验值总体较为符合。拟合结果与误差范围如图5和图6所示，其中最大误差出现在0 ℃下的20次循环处，误差值为-2.979%。

图5

新窗口打开| 下载原图ZIP| 生成PPT

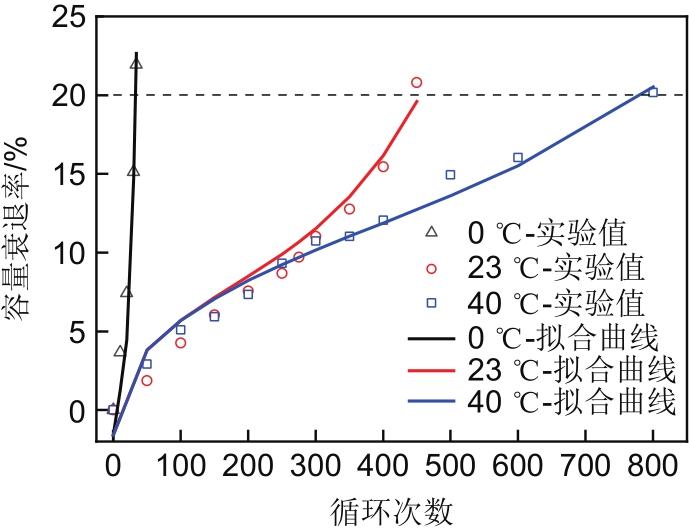
图5 C1D1工况下的容量衰退拟合结果

Fig. 5 Fitting results of capacity decline under C1D1 condition

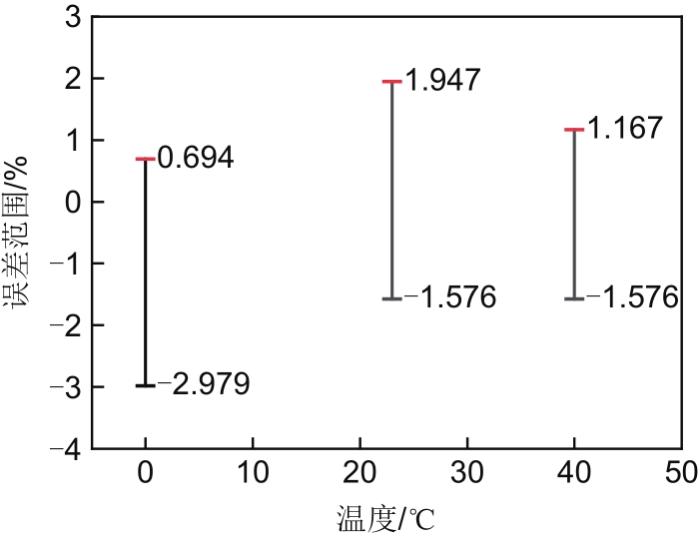
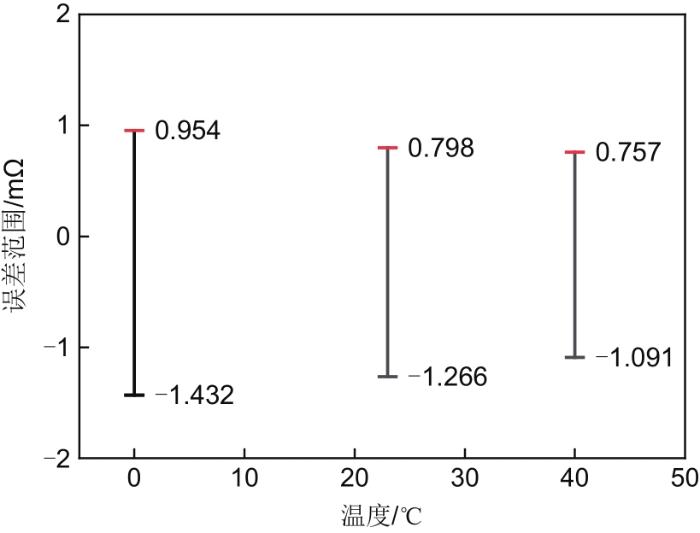
图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 C1D1工况下的容量衰退拟合误差范围

Fig. 6 The fitting error range of capacity decline under C1D1 condition

（2）在C1D2工况下进行拟合与验证

由于实验数据有限，在C1D2工况下采用交叉验证的方法验证公式(6)的准确性，即利用任意两个温度下的实验数据进行建模，再用第三个温度下的实验数据进行验证，得到的结果如表2所示，其中“0+23 ℃-40 ℃”的含义为使用0 ℃和23 ℃下的数据进行建模得到各个待拟合参数的值，并在40 ℃下进行验证，得到拟合优度R-square的值，另外两个工况同理。

表2 容量衰退模型交叉验证结果

Table 2 Capacity decay model cross-validation results

参数	0+23 ℃-40 ℃	0+40 ℃-23 ℃	23+40 ℃-0 ℃
D	0.013	0.0119	0.0115
E	3.94	3.968	3.899
F	-75.53	-76.46	-65.49
G	11380	11750	8310
H	166.1	169.2	141.4
I	0.432	0.4305	0.422
J	-0.9555	-0.9545	-0.6476
R-square	0.9840	0.9824	0.9833
RMSE	1.0757	1.0663	1.1012

新窗口打开| 下载CSV

从交叉验证结果可以看出，式(6)的容量衰退半经验模型具有很好的适用性，在各个工况下的拟合优度都大于0.98，因此经验模型精度较高，能够用于预测电池在C1D1和C1D2实验工况循环时，在不同温度下的容量衰退情况，有利于减少探究电池老化所需的实验时间与工作量。

2.2.2　结合温度、循环次数和放电倍率建立模型

在电池循环老化过程中，不同的充放电倍率下的容量衰退规律是不同的，而由于实验条件与实验时间的限制，本文只讨论放电倍率的影响。结合C1D1和C1D2两个工况的拟合结果，可以发现参数D、E和I在两个放电倍率下都很接近，推测其与放电倍率的相关性不大，而参数F、G、H和J在两个放电倍率下差异很大，推测其受放电倍率的影响较大。因此，本文建立的容量衰退半经验模型适用于C1D1和C1D2充放电工况下的不同温度条件，在其他充放电倍率下具有一定的适用性，其参数变化规律需要进一步探究。

2.3　不同温度条件下的容量衰退预测

由2.2节可知本文建立的电池容量衰退半经验模型可以用于预测电池在不同温度条件下的老化规律，因此利用式(6)预测电池在15 ℃、30 ℃和45 ℃下的容量衰退情况，如图7所示。

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 容量衰退率预测结果

Fig. 7 Forecast results of capacity decline rate

从图7可以看出温度越高电池容量衰退越慢，在45 ℃下老化时能够循环近900次。除了在45 ℃下的循环老化后期，其余工况下电池按照C1D1循环时的容量衰退曲线均在按照C1D2工况循环时的老化曲线下方，即小倍率循环时电池容量衰退速率较低。电池在45 ℃循环时，两种工况下的老化曲线差异相比于其他温度下较小，推测是由于电池在相对较高的温度下循环时，大倍率放电产生的热量影响减小，因此两个工况之间的容量衰退特性差异较小。

3 内阻增长实验结果分析

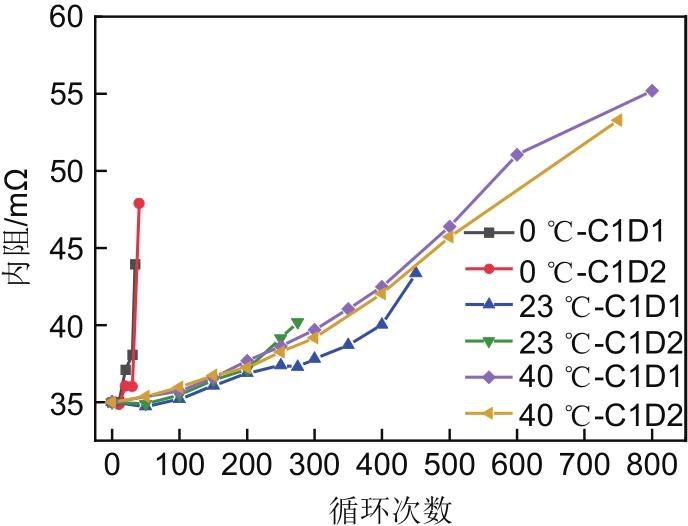
图8为电池在环境温度为0 ℃、23 ℃和40 ℃时，进行循环老化实验的过程中获得的电池内阻增长情况，电池充电电流为1 C，放电电流分别为1 C和2 C。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 电池内阻增长测试结果

Fig. 8 Battery internal resistance growth test results

3.1　影响电池内阻增长的因素

从图8中可以看出，随着循环次数的增加电池的内阻也逐渐增加。在23 ℃和40 ℃循环时，电池内阻的增长速率较慢且在前期基本重合。在0 ℃和40 ℃时，C1D1和C1D2工况的内阻增长曲线非常接近，此时电池内阻增长的趋势和规律基本不受放电倍率的影响。而在23 ℃时，C1D1和C1D2工况在前200次循环中内阻增长很接近，而200次循环后差异逐渐增大。观察图像还可以看出在0 ℃和40 ℃下循环老化时，C1D1工况的内阻增长曲线基本处于C1D2工况的内阻曲线上方，而在23 ℃循环时则相反，可见不同放电倍率下内阻增长的规律同样受温度影响。

3.2　建立内阻增长半经验模型

3.2.1　结合循环次数建立半经验模型

从图8中可以看出，在不同的工况下内阻增长的曲线趋势与容量衰退不同，所有工况下都近似为向上翘的指数函数，因此首先在不同工况下按照式(9)的形式对内阻进行拟合，拟合结果如表3所示。

R_{n} = K * e^{\frac{L}{n - M}} + P

(9)

式中，R_n 为只考虑循环次数时的内阻。K、L、M和P为待拟合参数，n为循环次数。

表3 各工况下按式(9)的拟合结果

Table 3 Fitting results according to Equation (9) in each working condition

工况	K	L	M	P	R-square
0 ℃-C1D1	9.89E6	-975.3	-35.52	35.49	0.9400
0 ℃-C1D2	73.09	-1128	-35.58	35.59	0.9408
23 ℃-C1D1	57.36	-886.4	-35.69	35.74	0.9921
23 ℃-C1D2	1.40E7	-1053	-35.38	35.38	0.9866
40 ℃-C1D1	49.52	-709	-35.04	35.1	0.9892
40 ℃-C1D2	56.77	-928.4	-35.72	35.66	0.9947

新窗口打开| 下载CSV

从表3可以看出内阻R_n 与循环次数n之间的指数关系较强，其中M和P近似互为相反数，系数K的变化范围很大，推测其受温度影响较大，而系数L、M和P的变化范围较小，可近似看作一个定值，与温度和放电倍率无关。

3.2.2　结合循环次数与温度建立半经验模型

由于系数K与温度的关系较大，且由前文可知温度对电池老化的影响是指数型的，因此在式(9)模型的基础上引入一个包含温度影响的指数函数，从而耦合循环次数和温度的影响，公式模型如式(10)所示。

R = S e^{\frac{U}{T + V}} e^{\frac{W}{n + Z}} + Z

(10)

式中，R为内阻的预测值，S、U、V、W和Z为待拟合参数。

（1）C1D1工况下的拟合

由3.2.1节可知，参数W和Z近似为定值，与温度和放电倍率无关，经过比较分别取-915和35.38时拟合效果较好，在C1D1工况下利用MATLAB的工具箱进行拟合，拟合公式如式(11)所示，拟合结果与误差范围如图9和图10所示。

R_{C 1 D 1} = 93.5 * e^{\frac{- 16.13}{T - 1.5}} * e^{\frac{- 915}{n + 35.38}} + 35.38

(11)

式中，R_C1D1为电池在C1D1工况下的内阻预测值。

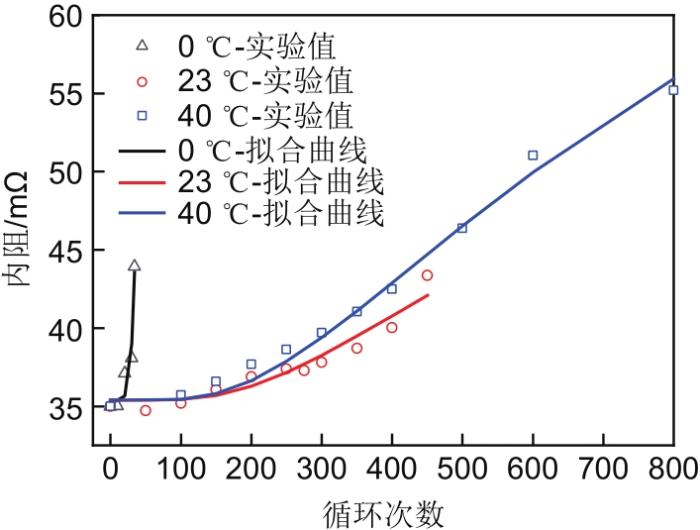
图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 C1D1工况下的内阻增长拟合结果

Fig. 9 Fitting results of internal resistance growth under C1D1 condition

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 C1D1工况下的内阻增长拟合误差范围

Fig. 10 The fitting error range of internal resistance growth under C1D1 condition

式(11)的R-square和RMSE分别为0.9814和0.7007。最大误差出现在0 ℃循环20次时，误差为-1.432 mΩ，其他大部分数据点的误差都在1 mΩ之内，精度较高。

（2）在C1D2工况下进行拟合与验证

为验证半经验公式模型(10)的准确性，与上文2.2.1节类似，采用C1D2工况中三个温度条件下的内阻实验数据进行交叉验证，用两个温度下的实验数据建模，并用第三个温度下的实验数据进行检验，计算结果如表4所示。

表4 内阻增长模型交叉验证结果

Table 4 Results of cross validation of internal resistance growth model

参数	0+23 ℃-40 ℃	0+40 ℃-23 ℃	23+40 ℃-0 ℃
S	28.02	28	27.97
U	30.24	30.59	30.97
V	2.691	2.703	2.716
W	-908.6	-915	-922.3
Z	35.34	35.38	35.42
R-square	0.9894	0.9894	0.9893
RMSE	0.5497	0.5348	0.5371

新窗口打开| 下载CSV

从表4可以看出，在C1D2工况的不同温度条件下，各个参数较为稳定，且拟合优度均大于0.98，因此本文建立的内阻增长模型具有较好的适用性，能够预测电池在不同温度下的内阻增长规律，缩短探究电池老化性能所需的实验时间。

3.2.3　结合温度、循环次数和放电倍率建立模型

由前所述，放电倍率对电池内阻增长规律的影响不可忽视，但由于实验数据的限制，难以将放电倍率耦合到内阻增长的半经验模型中。但观察C1D1和C1D2工况下的拟合结果，可以发现参数S、U和V在不同的放电倍率下的差异比较明显，推测其受放电倍率的影响较大，而参数W和Z并没有显著变化，因此推测其受放电倍率的影响较小，需要结合实验进一步探究。因此，本文所建立的内阻增长半经验模型能够适用于C1D1和C1D2工况的不同温度条件，有利于预测电池在不同工况下的内阻变化规律，避免进行大量的老化实验，缩短实验周期。

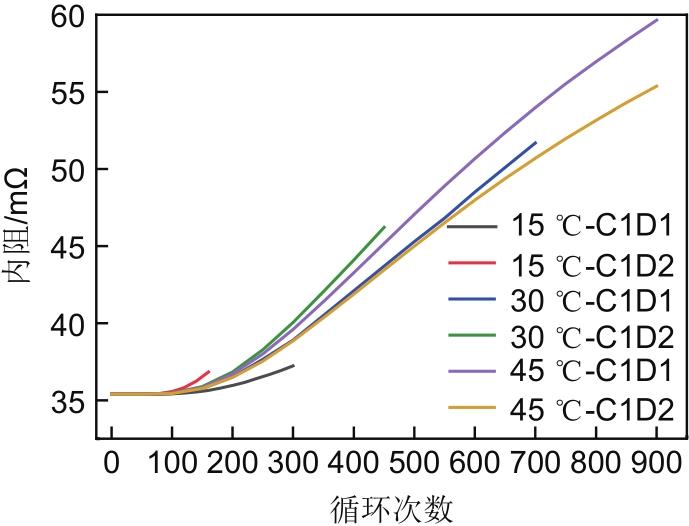
3.3　不同温度条件下的内阻增长预测

为了在不进行大量重复实验的基础上获得电池在其他温度条件下的内阻增长结果，与2.3节类似地采用式(8)对15 ℃、30 ℃和45 ℃三种温度下的内阻增长规律进行预测，结果如图11所示。

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 内阻增长预测结果

Fig. 11 Forecast results of internal resistance growth

从图11可以看出电池在15 ℃和30 ℃循环时，C1D2工况下的内阻增长曲线始终在C1D1工况下的内阻曲线上方，即此时以大倍率放电加剧了内阻的增长，而在45 ℃下循环时则相反。此外，在电池内阻增加的过程中并没有出现如图8中在0 ℃循环时迅速增长的趋势，因此可以推断电池只有在低温下循环时内阻才会显著增长，在其余温度循环时内阻增长较慢。此外结合图7可以看出，电池循环时的温度越高，其容量衰退20%左右时的内阻增长越大，因此温度是对电池内阻增长影响最大的因素。

4 结论

本文通过对高能量密度21700锂离子电池进行老化实验与性能测试，建立了电池老化半经验模型，并预测了电池在不同工况下的老化情况，主要获得了以下几点结论：

（1）通过实验可知温度越高电池的使用寿命越长。电池在23 ℃下循环老化时，不同放电倍率下的容量与内阻变化规律差异较大，电池在40 ℃下循环老化时，容量衰退率随着循环次数的增加不断放缓；

（2）通过引入两个关于循环次数的幂函数和常数项，建立了电池容量衰退半经验模型，通过分析可知适用于容量衰退曲线在不同温度下表现出不同趋势的情况，并在C1D2工况的不同温度下进行了交叉验证，精度较高；

（3）通过双指数函数累乘的方式，建立了预测电池内阻增长的半经验模型，并通过交叉验证证明了模型的准确性；

（4）利用建立好的电池老化模型，预测了电池在15 ℃、30 ℃和45 ℃下的容量与内阻变化规律，发现在45 ℃下以不同倍率循环时的容量衰退特性差异较小，并且随着循环温度的提高，电池容量衰退20%时的内阻增长最大，因此温度是影响电池老化规律最主要的因素。

本文建模过程中所用到的工况数据有限，考虑到电池老化实验耗时较长，后续计划开展更多放电倍率与充电倍率下的实验，并在其他类型的电池上进一步拓展所建立的半经验模型的适用范围。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

林名强, 吴登高, 郑耿峰, 等. 基于表面温度和增量容量的锂电池健康状态估计[J]. 汽车工程, 2021, 43(9): 1285-1290, 1284.

[本文引用: 1]

LIN M Q, WU D G, ZHENG G F, et al. Estimation method of state of health of lithium battery based on surface temperature and incremental capacity[J]. Automotive Engineering, 2021, 43(9): 1285-1290, 1284.

[本文引用: 1]

[2]

WEI J W, DONG G Z, CHEN Z H. Remaining useful life prediction and state of health diagnosis for lithium-ion batteries using particle filter and support vector regression[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5634-5643.

[本文引用: 1]

[3]

任璞, 王顺利, 何明芳, 等. 基于内阻增加和容量衰减双重标定的锂电池健康状态评估[J]. 储能科学与技术, 2021, 10(2): 738-743.

[本文引用: 1]

REN P, WANG S L, HE M F, et al. State of health estimation of Li-ion battery based on dual calibration of internal resistance increasing and capacity fading[J]. Energy Storage Science and Technology, 2021, 10(2): 738-743.

[本文引用: 1]

[4]

WALDMANN T, WILKA M, KASPER M, et al. Temperature dependent ageing mechanisms in Lithium-ion batteries - A Post-Mortem study[J]. Journal of Power Sources, 2014, 262: 129-135.

[本文引用: 1]

[5]

WANG J, LIU P, HICKS-GARNER J, et al. Cycle-life model for graphite-LiFePO₄ cells[J]. Journal of Power Sources, 2011, 196(8): 3942-3948.

[本文引用: 1]

[6]

LI Z, LU L G, OUYANG M G, et al. Modeling the capacity degradation of LiFePO₄/graphite batteries based on stress coupling analysis[J]. Journal of Power Sources, 2011, 196(22): 9757-9766.

[本文引用: 1]

[7]

LEWERENZ M, MÜNNIX J, SCHMALSTIEG J, et al. Systematic aging of commercial LiFePO₄ Graphite cylindrical cells including a theory explaining rise of capacity during aging[J]. Journal of Power Sources, 2017, 345: 254-263.

[本文引用: 1]

[8]

GUAN T, ZUO P J, SUN S, et al. Degradation mechanism of LiCoO₂/mesocarbon microbeads battery based on accelerated aging tests[J]. Journal of Power Sources, 2014, 268: 816-823.

[本文引用: 1]

[9]

GAO Y, JIANG J C, ZHANG C P, et al. Lithium-ion battery aging mechanisms and life model under different charging stresses[J]. Journal of Power Sources, 2017, 356: 103-114.

[本文引用: 1]

[10]

张金, 魏影, 韩裕生, 等. 一种锂离子电池容量退化经验模型[J]. 电源技术, 2016, 40(6): 1176-1179.

[本文引用: 1]

ZHANG J, WEI Y, HAN Y S, et al. Empirical capacity degradation model of lithium-ion battery[J]. Chinese Journal of Power Sources, 2016, 40(6): 1176-1179.

[本文引用: 1]

[11]

刘建, 李占锋, 屈薇薇. 不同应力作用下钴酸锂电池老化特性分析[J]. 电子元件与材料, 2019, 38(12): 38-42.

[本文引用: 1]

LIU J, LI Z F, QU W W. Aging analysis of lithium cobalt oxide batteries under different charge conditions[J]. Electronic Components and Materials, 2019, 38(12): 38-42.

[本文引用: 1]

... 近年来，新能源汽车产销量不断增加，而锂离子电池因具有绿色环保、能量密度高、无记忆效应以及自放电率低等优点成为了新能源汽车动力电池的首选.随着使用时间的不断累积，锂电池会不断地老化，表现为可用容量的逐渐衰减与内阻的不断增加^[1].一般当电池的容量衰退20%，或内阻增加一倍后就不再使用该电池^[2]，因此需要在使用过程中对电池的健康状态进行预测^[3].同时电池的内阻增长会导致电池在使用时产生更多的热量，严重时甚至会引发热失控.因此这两个性能参数与电池的使用寿命和安全性关系密切，对电池的老化研究至关重要. ...

... Waldmann等^[4]采用NCM/LMO混合正极电池在较大的温度范围内做了电池老化实验，发现除25 ℃以外，容量均近似线性衰减.Wang等^[5]考虑到LFP电池在不同DOD下循环时放电量的不同，结合Arrhenius公式，建立了容量与温度、倍率以及安时吞吐量的半经验模型.Li等^[6]除了关注温度与倍率外，还考虑了截止电压对LFP电池容量与内阻的影响，同时探究了双因素组合对电池老化的耦合作用，并结合Arrhenius公式与逆幂律公式建立多因素耦合的寿命预测模型.Lewerenz等^[7]研究发现LFP电池的容量衰退与内阻增长之间具有相关性，当容量偏离线性衰退时内阻快速增加.Guan等^[8]在30% DOD的实验条件下进行研究，发现循环倍率对LCO电池容量衰退的影响存在一个临界值，大于或小于该倍率都不会加深电池的老化.此外，Gao等^[9]发现对于LCO电池的老化过程，充电截止电压也存在一个临界值，当超过该临界值时容量与内阻变化剧烈，并据此建立了容量衰退关于充电电流与充电截止电压的半经验模型.张金等^[10]在双指数模型的基础上推导出更加简单的三参数容量衰退模型，提高了预测LCO电池老化程度的鲁棒性与实用性.刘建等^[11]建立的LCO电池容量衰退半经验模型不仅考虑了温度和循环倍率，还考虑了充电截止电压. ...

〈

〉