针对现有固体蓄热技术存在的蓄热体局部受热不均及实际蓄热能力偏低等问题,基于现有理论研究成果,本工作结合实际工程应用对固体蓄热器的蓄热体结构进行设计分析,建立一种新型结构蓄热体,利用ANSYS Workbench模块下的Steady-State Thermal和Transient Thermal对建立的新型结构蓄热体与传统结构蓄热体进行对比研究,得到两种蓄热体结构在相同蓄热时间下的温度分布规律和目标蓄热温度下的实际蓄热能力[9]。
1 蓄热体模型构建
1.1 结构模型
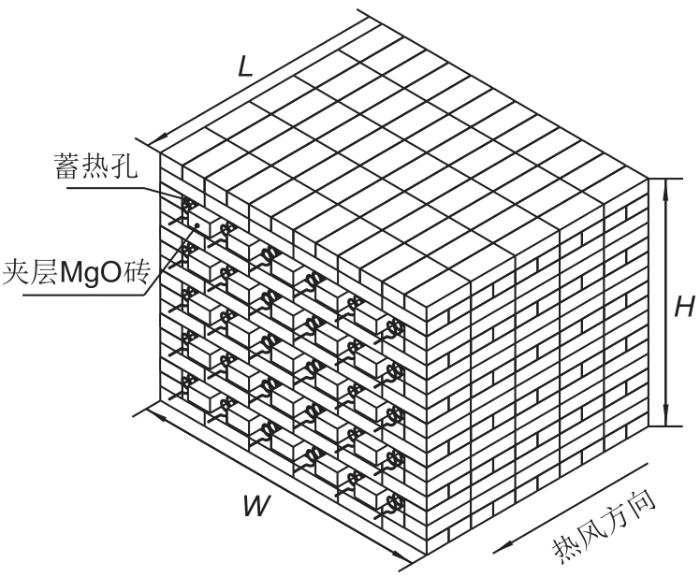
图1
图2
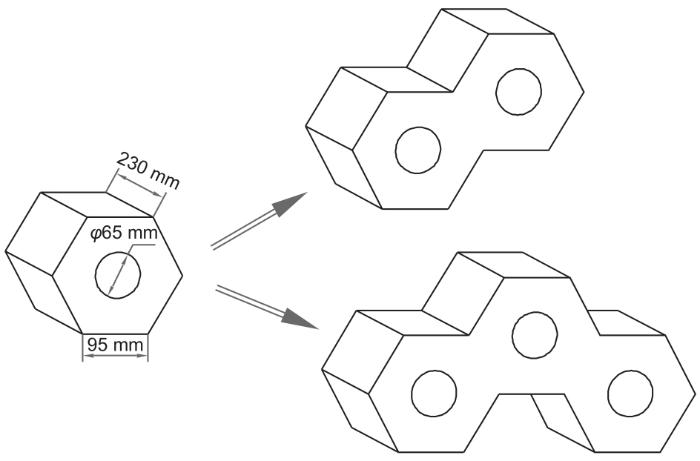
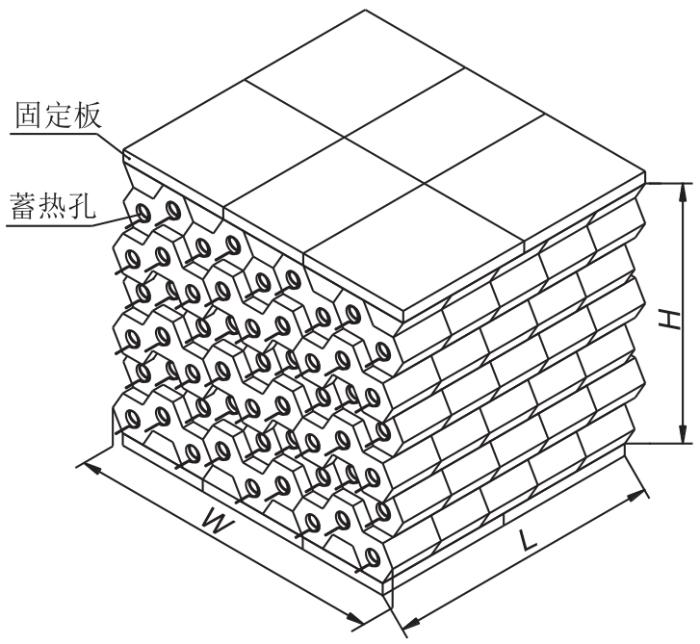
考虑到传统结构蓄热体的蓄热孔为堆砌形成,壁面接触会形成热阻,新型砖体蓄热孔采用直接加工成型的方式,消除壁面接触热阻的影响;为解决电阻丝对蓄热孔周围砖体加热距离不等的问题,同时考虑蓄热体结构搭建稳定性,新型砖体采用正六边形结构,圆形蓄热孔位于正六边形中心。砖体结构如图3所示,最小蓄热单元MgO砖截面形状为正六边形,边长95 mm,砖体中心设有直径为65 mm的蓄热孔,用于放置电阻丝加热蓄热体,砖体厚度为230 mm。
图3
图4
图5
1.2 数学模型
结合蓄热过程的传热学理论及蓄热体结构特点,对蓄热过程分析模型作如下处理:①忽略蓄热体内部MgO砖间的面接触热损失,蓄热体外壁面作绝热处理,与环境没有热量交换;②忽略辐射换热,用壁面热传导代替;③考虑到蓄热体纵向分布一致性,故取蓄热体模型的1/10进行蓄热分析。
该蓄热体的蓄热过程属于具有内热源
式中,
由于蓄热介质MgO砖的热物理参数随温度、蓄热时间等影响较大,采用定值处理进行蓄热分析易产生仿真误差,故此处采用非定值仿真分析方法。在非定值处理的各参数中,密度几乎不随固体材料的温度变化而变化,通过Solidworks模型质量属性读取标砖实际体积以及称重法测量得到MgO砖实际密度
式中,
2 蓄热过程对比分析
本工作利用ANSYS Workbench模块下的Steady-State Thermal和Transient Thermal分析方法对新型结构蓄热体与传统结构蓄热体的蓄热过程进行对比仿真分析。两种蓄热体结构数值模拟对比分析中,设计蓄热时间10 h,蓄热起始温度373 K,蓄热终止温度873 K。根据传热学理论可算出两种蓄热体结构的理论蓄热容量,再通过数值模拟结果,即可对两种蓄热体结构的实际蓄热量、蓄热时间及温度分布情况进行对比分析。
2.1 无关性验证
表1 网格划分
Table 1
| 相关参数 | 网格划分1 | 网格划分2 | 网格划分3 |
|---|---|---|---|
| 传统结构蓄热体 | 72028 | 125363 | 185693 |
| 新型结构蓄热体 | 183001 | 316236 | 453596 |
表2 步长划分
Table 2
| 相关参数 | 步长1/s | 步长2/s | 步长3/s |
|---|---|---|---|
| 传统结构蓄热体 | 600 | 300 | 150 |
| 新型结构蓄热体 | 600 | 300 | 150 |
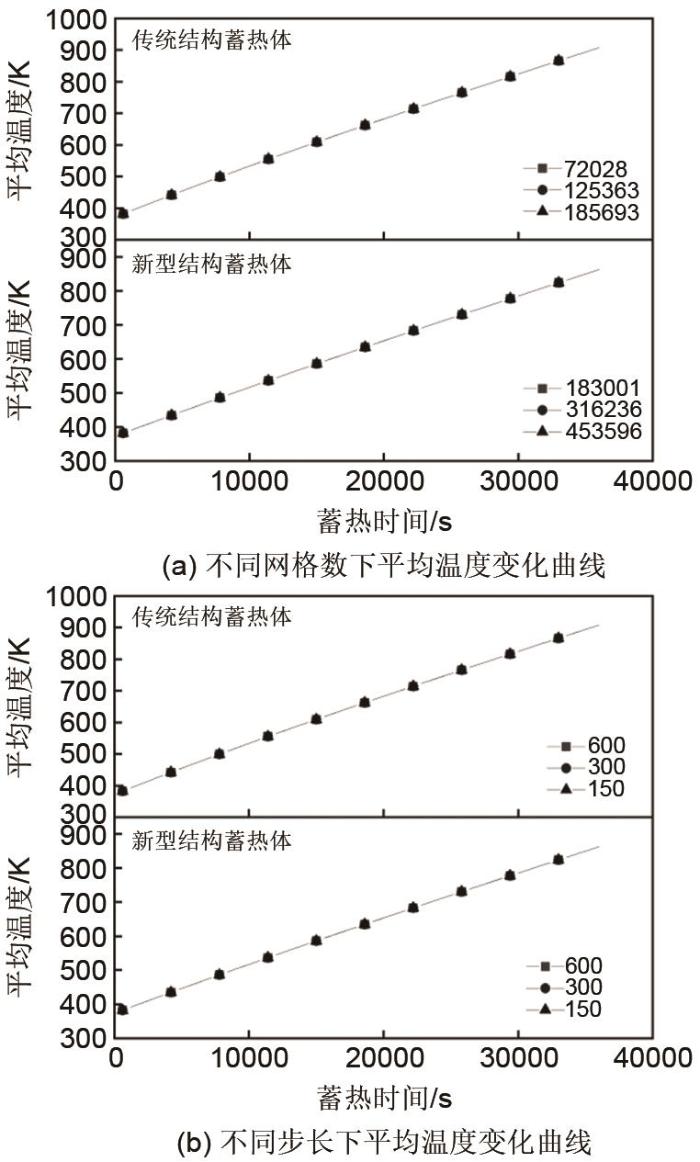
通过对蓄热过程的数值模拟,得到两种蓄热体结构在不同网格数及步长下物理模型平均温度随时间的变化曲线如图6所示。
图6
从图6可以看出,不同网格划分数及不同步长设定下,两种物理模型数值模拟结果的平均温度随时间变化曲线基本重合,网格数增加和步长缩短对数值模拟结果影响不大。为提高计算效率,在满足计算精度的情况下,本工作选取传统结构蓄热体网格数72028,新型结构蓄热体网格数183001,时间步长600 s进行蓄热过程数值模拟分析。
2.2 蓄热温度对比分析
蓄热容量指单位体积(或质量)下,蓄热体热储存容量,计算公式为:
式中,
设计蓄热时间10 h,蓄热温差500 K,结合蓄热体体积参数,根据式(
表3 对比分析参数表
Table 3
| 相关参数 | 传统结构蓄热体 | 新型结构蓄热体 |
|---|---|---|
| MgO砖密度/(kg/m3) | 2796 | 2796 |
| 蓄热体尺寸/m | 1.38×1.15×1.11 | 1.33×1.20×1.07 |
| 理论蓄热容量/(kWh) | 626.42 | 560.91 |
| 加热孔数量 | 30 | 54 |
| 加热孔截面尺寸/mm | 97×65 | φ65 |
| 总砖隙比 | 7.10 | 6.66 |
| 单孔加热功率/kW | 2.09 | 1.04 |
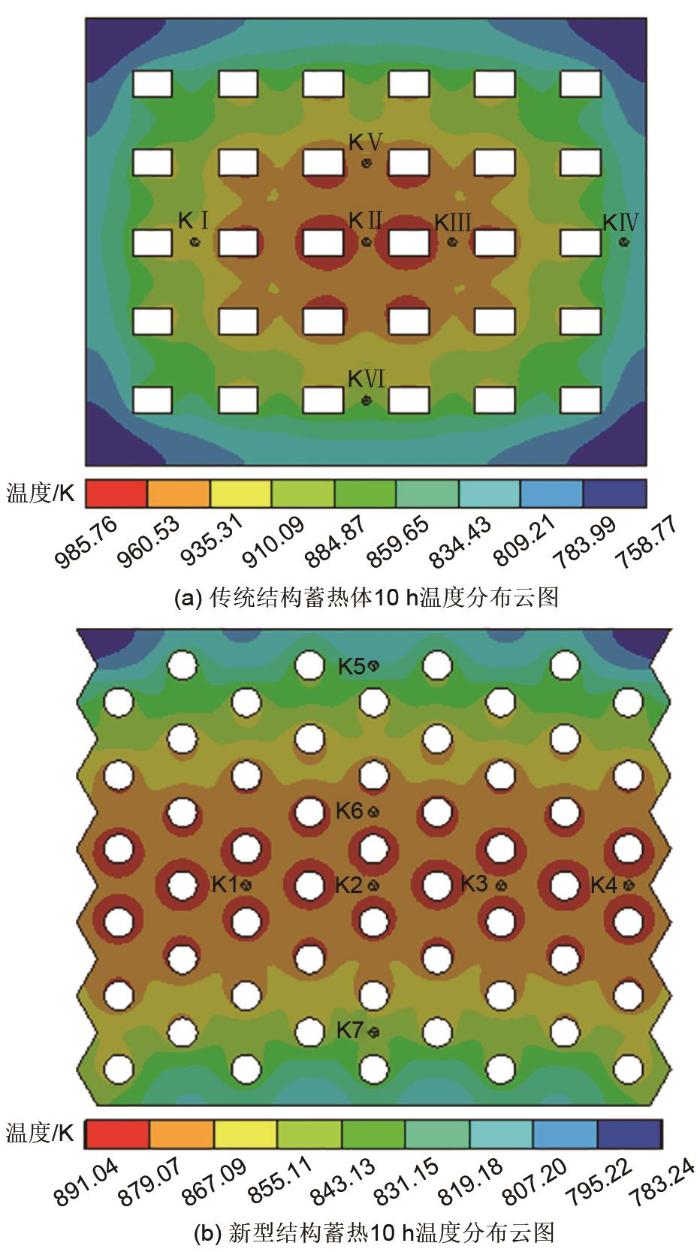
首先对两种蓄热体结构进行定容比较分析,由于两种蓄热体结构不同,则通过公式计算得到的理论蓄热容量不同,但两种蓄热体结构的设计蓄热时间及蓄热温差相等,所以可根据理论蓄热容量计算结果,设定传统与新型蓄热体结构模型的蓄热功率分别为6.26 kW和5.60 kW,蓄热功率平均分布到各个蓄热孔内热源加热蓄热体。最终得到两种蓄热体模型目标蓄热10 h时的温度分布情况如图7所示。KⅠ~KⅥ与K1~K7分别为传统结构蓄热体与新型结构蓄热体分析模型的模拟温度监测点。
图7
图7
蓄热10 h温度分布对比图
Fig. 7
Temperature comparison diagram for a 10-hour heat storage
从蓄热体结构方面分析,传统结构蓄热体蓄热孔截面形状为矩形,矩形蓄热孔横纵方向对齐排列,但横向蓄热孔与纵向蓄热孔间堆砌的MgO砖层数不同,则电阻丝对蓄热孔周围各层MgO砖的加热距离不等,易导致蓄热体温度分布不均,产生较大温度梯度,所以传统结构蓄热体的温差值较大;新型结构蓄热体蓄热孔截面形状为圆形,且蓄热孔纵向交错排列,相邻蓄热孔等距排布,则电阻丝对砖体的加热厚度各向相等,所以新型结构蓄热体的温差值较低,整体温度分布更加均匀。
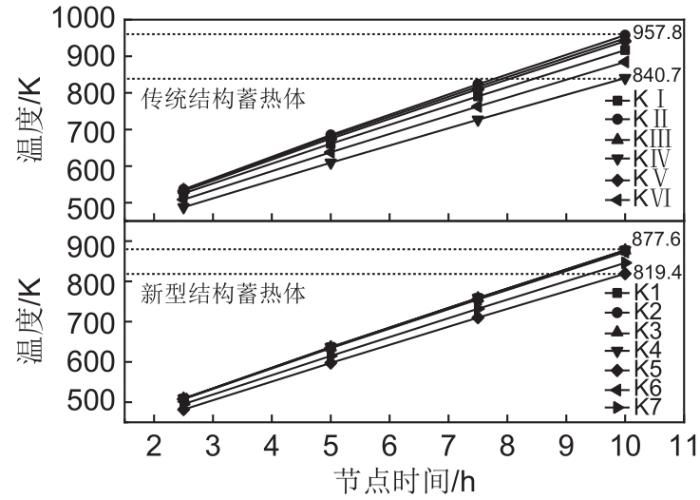
表4 传统结构蓄热体节点时间温度分布
Table 4
| 时间/h | 温度/K | |||||
|---|---|---|---|---|---|---|
| KⅠ | KⅡ | KⅢ | KⅣ | KⅤ | KⅥ | |
| 2.5 | 525.4 | 536.5 | 535.0 | 487.6 | 531.9 | 508.6 |
| 5 | 661.1 | 685.0 | 680.4 | 609.4 | 675.0 | 638.0 |
| 7.5 | 790.7 | 823.8 | 816.9 | 726.7 | 810.3 | 763.1 |
| 10 | 916.8 | 957.8 | 949.0 | 840.7 | 941.3 | 884.8 |
表5 新型结构蓄热体节点时间温度分布
Table 5
| 时间/h | 温度/K | ||||||
|---|---|---|---|---|---|---|---|
| K1 | K2 | K3 | K4 | K5 | K6 | K7 | |
| 2.5 | 508.7 | 508.7 | 508.7 | 508.9 | 481.9 | 507.7 | 495.2 |
| 5 | 636.4 | 636.3 | 636.4 | 636.8 | 597.5 | 634.1 | 615.1 |
| 7.5 | 758.3 | 758.2 | 758.3 | 758.9 | 710.0 | 755.1 | 732.1 |
| 10 | 876.9 | 876.7 | 876.9 | 877.6 | 819.4 | 873.0 | 846.1 |
图8
通过对两种蓄热体模型温度监测点数据分析可知,传统结构蓄热体6个监测点中靠近蓄热体中心区域的KⅡ、KⅢ、KⅤ温度值和温升曲线在蓄热初期重合度较高,随着时间的推移,曲线重合度降低,而处于蓄热体外围区域的KⅠ、KⅣ、KⅥ温度偏差率达到12.3%;新型结构蓄热体7个监测点中整个蓄热体中部的K1~K4、K6点温度值和温升曲线在蓄热全过程基本一致,处于蓄热体外围区域的K5、K7温度偏差率仅为6.6%,相比于传统结构蓄热体,各个监测点的温升趋势更加接近。
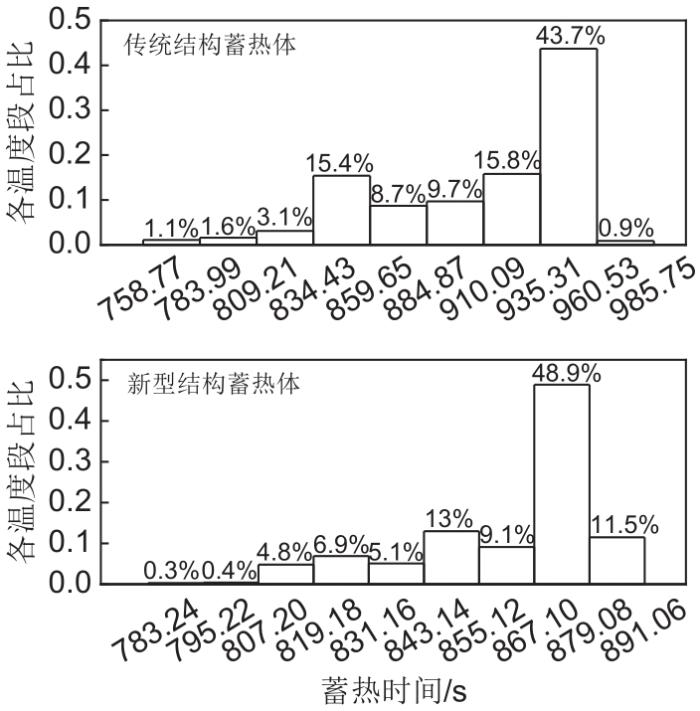
图9为蓄热10 h传统结构蓄热体与新型结构蓄热体各温度段的网格节点温度分布占比图。
图9
由图9可以看出,蓄热10 h时传统结构蓄热体的节点温度在设计蓄热温度873 K附近的859.65~884.87 K区间占比仅为8.7%,而在高温段884.87~985.75 K区间占比达到70.1%,整体温度分布不均,局部温度过高会使温度传感器提前控制电阻丝停止加热,缩短蓄热体蓄热时间,则会影响整个蓄热体的蓄热容量;新型结构蓄热体的节点温度主要集中分布在设计蓄热温度873 K附近的867.10~891.06 K区间内,占比达到60.4%,未形成明显的高温段,整体温度分布更加合理,蓄热体蓄热时间更长,实际蓄热能力更好。
2.3 蓄热容量对比分析
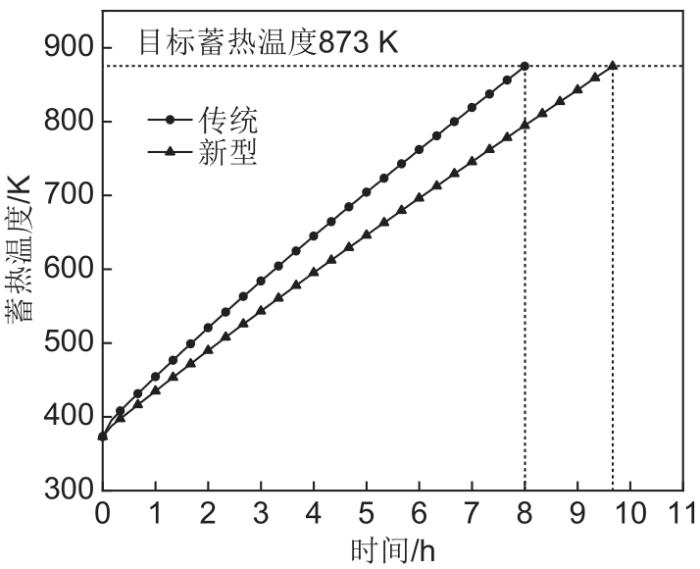
结构改善后的新型结构蓄热体,蓄热孔内电阻丝对MgO砖的加热更加充分,其相应的蓄热时间及理论热容率将得到提升,当蓄热体达到目标蓄热温度时,蓄热体内布置的传感器控制电阻丝停止加热,结束蓄热过程。图10为两种蓄热体结构在相同边界条件下的蓄热过程温升曲线。
图10
从图10可以看出,在相同目标蓄热温度下,传统结构蓄热体的蓄热时间为8.0 h,而新型结构蓄热体的蓄热时间为9.6 h,结合蓄热过程两种蓄热体模型设定功率值可知,新型结构蓄热体的实际蓄热能力更好。
表6为两种蓄热体结构达到目标蓄热终止温度873 K时的相关参数对比。
表6 终止温度873 K参数对比
Table 6
| 相关参数 | 传统结构蓄热体 | 新型结构蓄热体 |
|---|---|---|
| 蓄热起始温度/K | 373 | 373 |
| 蓄热终止温度/K | 873 | 873 |
| 蓄热时长/h | 8.0 | 9.6 |
| 实际蓄热容量/kWh | 501.14 | 538.47 |
| 达到理论热容率 | 80% | 96% |
从表6可以看出,达到目标蓄热终止温度873 K时,新型结构蓄热体的实际蓄热容量达到理论蓄热容量的96%,而传统结构蓄热体的实际热容量仅有其理论热容量的80%。结合蓄热体结构参数分析,新型结构蓄热体单位体积蓄热容量提升了20%,即在相同的蓄热容量情况下,体积仅有传统结构蓄热体的83%,能有效减少蓄热体占地面积,提高资源利用率,相应减少用户初安装成本,有利于市场推广。
3 结论
本工作以碱性耐火材料MgO砖作为蓄热介质,设计一种新型结构蓄热体,通过对两种蓄热体结构在相同蓄热时间下的温度分布规律和目标蓄热温度下的实际蓄热能力进行对比分析,得到以下结论。
(1)目标蓄热时间下,传统结构蓄热体整体温差值为227.0 K,监测点温度偏差率达12.3%,节点温度在高温段占比达70.1%,设计蓄热温度873 K温度段占比仅8.7%;新型结构蓄热体整体温差为107.8 K,监测点温度偏差率为6.6%,节点温度在设计蓄热温度873 K温度段占比60.4%,未形成明显高温段,整体温度分布更加合理。
(2)目标蓄热温度下,新型结构蓄热体的实际蓄热容量达到理论蓄热容量的96%,较传统结构蓄热体提升16%,同时体积仅有传统结构蓄热体的83%,能有效减少蓄热体占地面积,相应降低蓄热成本,有利于市场推广。
参考文献