国内外对电热储能装置进行了大量研究,文献[3]利用流固耦合传热模型将难以确定的热流边界转化为系统内部边界,对固体电蓄热装置温度场及应力场分布进行分析。文献[4]采用流固耦合的方法对固体蓄热结构传热机理进行分析,从通道结构、孔隙率及进口空气流速等方面对蓄热结构进行优化,并采用优化后蓄热结构参数搭建实验平台进行蓄热结构性能测试。文献[5]利用TRNSYS软件对房屋建筑的周围环境以及气候进行分析、对小型电磁采暖装置进行探究并且进行模拟分析,模拟结果显示,相比于传统的电磁采暖系统,能够节约25%~30%的能量损耗。文献[6-9]以熔盐电磁感应加热器为研究对象,利用数值模拟方法研究不同加热条件下感应加热器壁面以及熔盐内部磁场和温度场的分布特点,并得到线圈电流、电流频率、熔盐流速和加热器材料对磁场和温度场的影响规律。目前,电热储能装置主要采用电阻式加热,虽然这种方式被广泛使用,但其加热时间长、加热温度不均匀、加热电阻丝使用寿命短、易老化等缺点仍无法解决。
针对以上问题,本工作根据已有的固体电热储能装置的基本原理以及实际基础,将电磁感应加热技术应用在固体电热储能装置中,并在某企业搭建一套采用感应加热的新型电热储能实验装置,同时利用COMSOL模拟其蓄热过程。实验结果表明采用感应加热可以提高加热速度且均温性更好,在加热阶段通过改变流场流速可以改善蓄热体温度分布,从而提升系统效率,为感应加热电热储能装置的研究与开发提供一定的理论依据。
1 装置工作原理
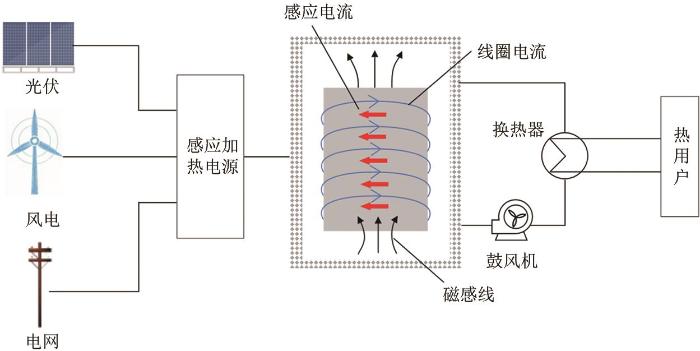
本工作研究的电热储能装置可用于新能源消纳以及居民供暖等领域。装置主要由蓄热体、感应加热线圈、感应加热电源、换热器、循环风机等组成,其换热方式与电阻式电热储能装置类似:蓄热时,利用低谷电通过感应加热线圈将电磁能转换为热能储存在蓄热体中;释放时,低温气体通过循环风机在换热通道与蓄热体表面发生接触,蓄热体内储存的热量通过对流换热的方式将低温气体加热,被加热的低温气体再通过换热器将热量转移给热用户。与传统电阻式电热储能装置不同,本工作提出的固体电热储能装置利用铸铁为储热介质,其优势是可一体化成型,能够有效降低生产成本。装置工作原理如图1所示。
图1
图1
感应加热固体蓄热装置工作原理
Fig. 1
Schematic diagram of the working principle of induction heating solid heat storage device
法拉第电磁感应定律指出:当通过闭合回路的磁通量发生变化时,在导体内部就会产生感应电动势e,计算公式为:
式中,N为线圈匝数,其大小与穿过回路的磁通量随时间变化率成正比。
当线圈通过交流电流时,线圈周围会产生交变磁场,从而产生感应电流——涡流。涡流大小取决于磁场强度,其在紧靠线圈附近最强,并随距离的平方而减小。由于趋肤效应的影响,电流仅通过导体的表面层,表面层深度与导体性质和电流频率有关,通常将这一表面层的深度或厚度称为穿透深度。穿透深度为Δ,由
式中,f为交变电流频率;μr为相对磁导率;ρ为导体的电阻率。
由
2 数学模型与建模
2.1 几何模型
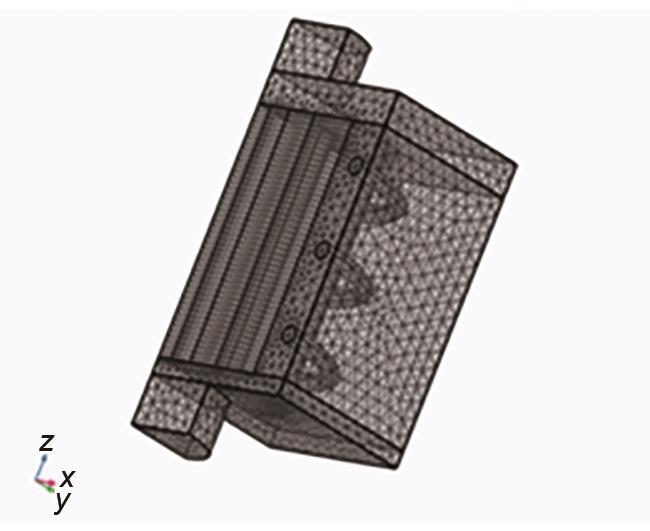
蓄热体整体为一个圆柱体,半径为0.75 m,高为1.5 m,总体积为2.5 m3,材料为铸铁材料。在其中心处共开设7个圆柱形风道,其中中心处为主风道,在主风道四周按圆周排列着一定数量与主风道大小相同辅助风道以提高传热效果。电热储能装置整体结构与实验装置如图2所示。其中感应加热线圈按一定距离均匀套在蓄热体上,外壳上下设置两个风道,与蓄热体散热通道对应分别用作进风、出风。
图2
图2
电热储能装置整体结构与实验装置
Fig. 2
Overall structure and experimental equipment of electric energy storage device
2.2 电磁场控制方程
麦克斯韦方程组是电磁场理论的基础,可以用其描述普遍存在的电磁场现象,对电磁场问题的研究最终都可以通过对方程组求解进行实现[10]。麦克斯韦方程组如下:
式中,ρ为体电荷密度; D 为电通密度; H 为体电荷密度; J 为传导电流密度; E 为电场强度; B 为磁感应强度。
场量之间介质的本构关系为:
式中,ε为空间介电常数;μ为磁导率;σ为导体材料的电导率。
2.3 流固耦合传热控制方程
(1)流体域控制方程
质量守恒方程:
动量守恒方程:
能量守恒方程:
式中, ρf为流体密度;v为流体时均速度;v'为脉动速度;h为流体焓;p为流体的静压; μf为湍流黏度。
(2)固体区域传热控制方程:
式中, ρs为固体密度;t为时间; λ 为热导率;c为比热容;Ts为固体温度; Φ 为固体内部体积热源。
(3)固体与流体边界条件
式中,qs、qf分别为流固交界面上固体热通量与流体热通量; λs、 λf为固体热导率与流体热导率;Ts、Tf分别为固体温度与流体温度;n为流固交界面法向量。
2.4 装置效率计算
加热过程中,蓄热体被加热过程中吸收的热功率Ps为储存在蓄热体内热量Qs与加热时间t之比:
式中,cs为铸铁比热容;m为铸铁质量;∆Ts为铸铁温升。
电源功率Pw计算公式为:
式中,U为三相电源电压有效值;I为三相电源电流有效值;cos φ 为电源功率因数,取0.85。
电热储能装置热转换效率η为:
3 仿真与讨论
本工作仅研究装置蓄热过程,为确定模型的蓄热特性,对模型进行合理简化:
(1)由于铸铁材料磁导率明显高于空气,故本工作不考虑漏磁及漏热情况;
(2)蓄热体材料为各向同性均匀介质;
(3)整个装置在设计时结构对称,故模拟装置的四分之一结构即得到整个蓄热装置温度分布,同时为缩短计算时间同时确保计算精度,网格数量为30万。装置网格如图3所示。
图3
表2 铸铁材料主要物理指标
Table 2
| 指标 | 参数值 |
|---|---|
| 热导率/[W/(m·K)] | 700 |
| 密度/(g/m3) | 7.0 |
| 电导率/(S/m) | 1 |
| 比热容/[kJ/(kg·K)] | 0.46 |
| 磁导率/(H/m) | 200 |
| 熔点/℃ | 1200 |
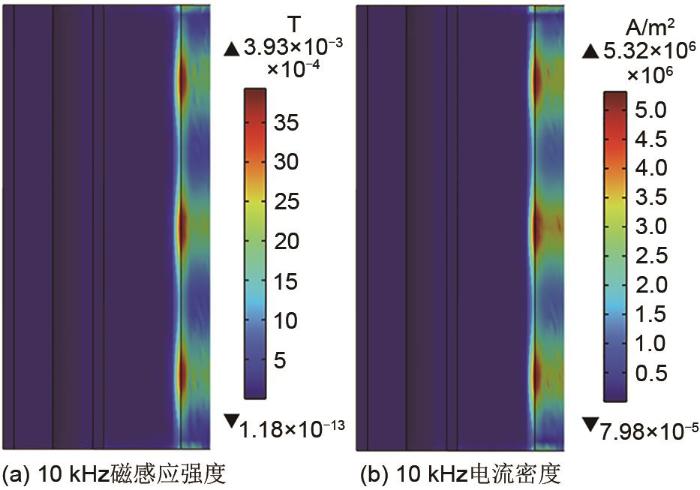
3.1 模型初始条件与电磁场及温度场分析
图4
图4
蓄热体表面磁感应强度与电流密度分布云图
Fig. 4
Magnetic induction intensity and current density distribution cloud of 10 kHz heat storage body
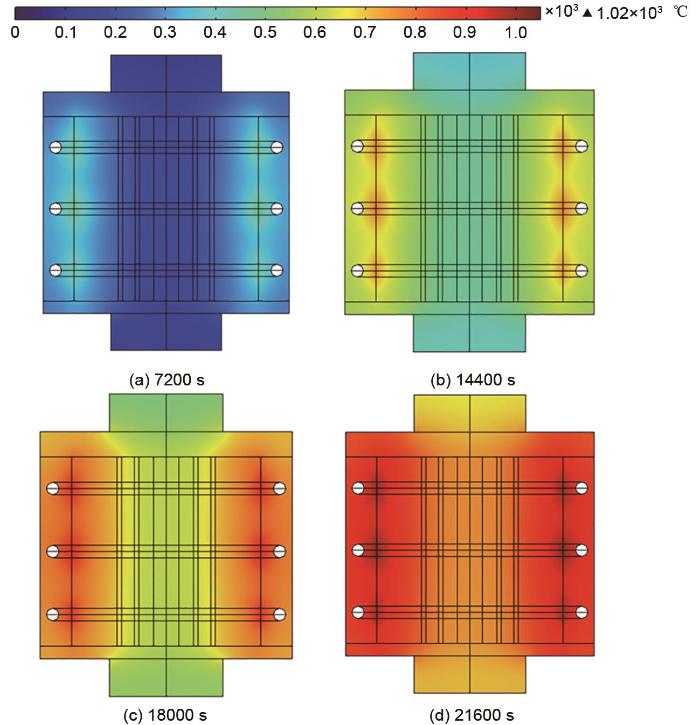
图5
图5
蓄热装置加热过程温度分布(z=0.75 m)
Fig. 5
Temperature distribution of heating process of heat storage device (z=0.75 m)
图6
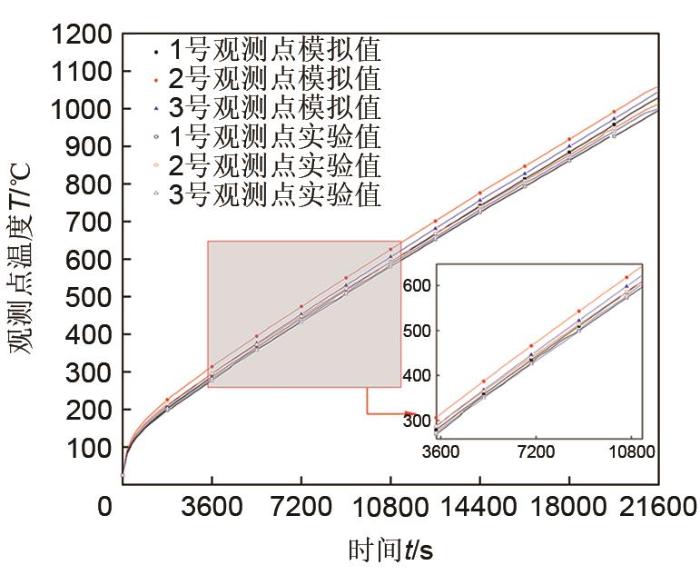
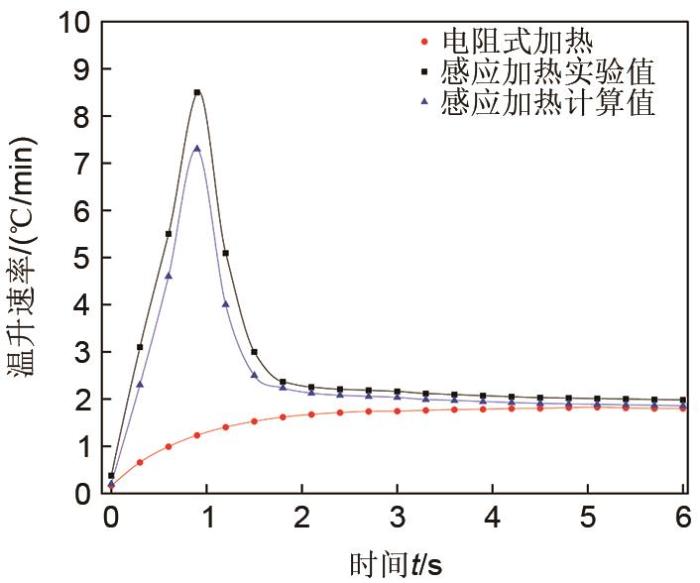
图7为不同加热方式下的蓄热体温升速率曲线,可以看出在初始加热阶段1 h内,感应加热的温升速率明显高于电阻式加热,其温升速率最大值为8.5 ℃/min,随后趋于稳定;在加热4 h左右后,两种加热方式的温升速率基本相同。因此,在未来电力市场中,感应加热具有快速响应电网的能力,能够实现与电网的实时互动。各观测点实验温度与计算温度上升速率变化不大,温度变化趋势也基本一致。计算数值与实验数值的误差主要来自于传感器的误差。
图7
图7
感应加热与电阻式加热温升速率曲线
Fig. 7
Temperature rise rate curve of induction heating and resistance heating
3.2 线圈频率对电磁场分布影响
图8
图8
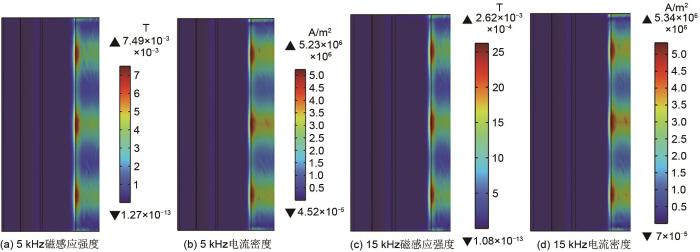
5 kHz与15 kHz磁感应强度与感应电流密度分布云图
Fig. 8
5 kHz and 15 kHz magnetic induction intensity and induced current density distribution clouds
表3 不同电流频率下蓄热体表面磁感应强度与感应电流密度最大值
Table 3
| 电流频率/kHz | 磁感应强度×10-3/T | 感应电流密度×106/(A/m2) |
|---|---|---|
| 5 | 7.49 | 5.23 |
| 10 | 3.93 | 5.32 |
| 15 | 2.62 | 5.34 |
图9
图9
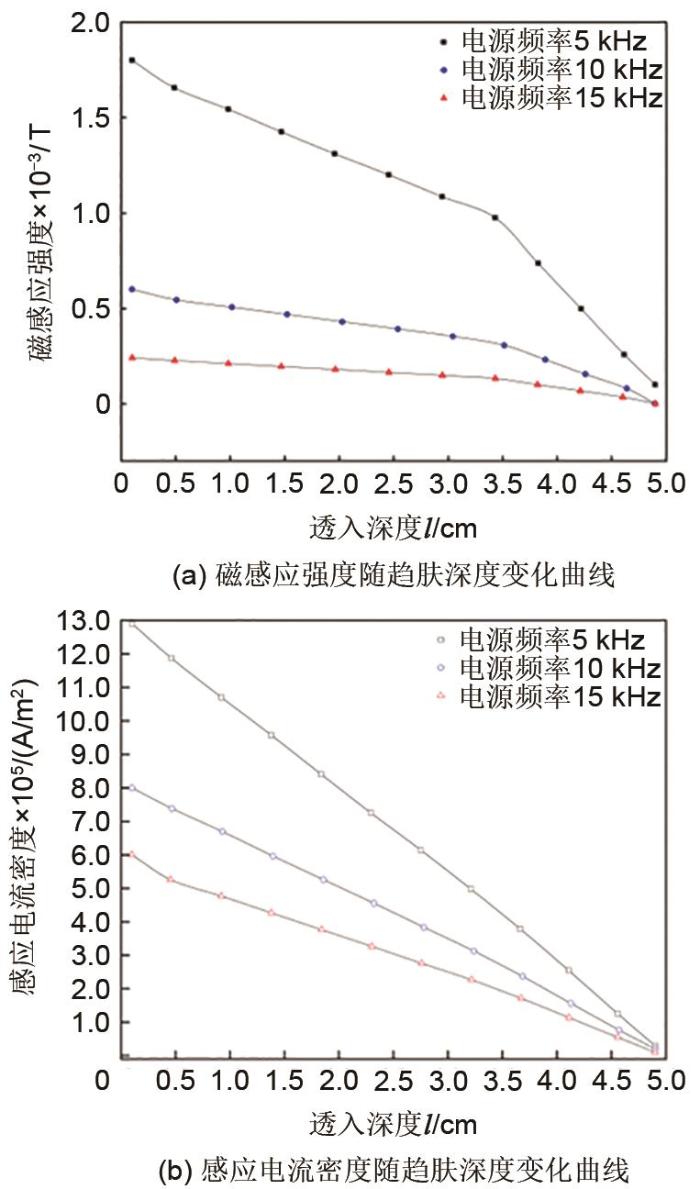
不同电流频率下磁感应强度与感应电流密度随趋肤深度变化曲线
Fig. 9
The magnetic induction intensity and induced current density change curve with skin depth at different current frequencies
3.3 线圈电流频率对温度场分布影响
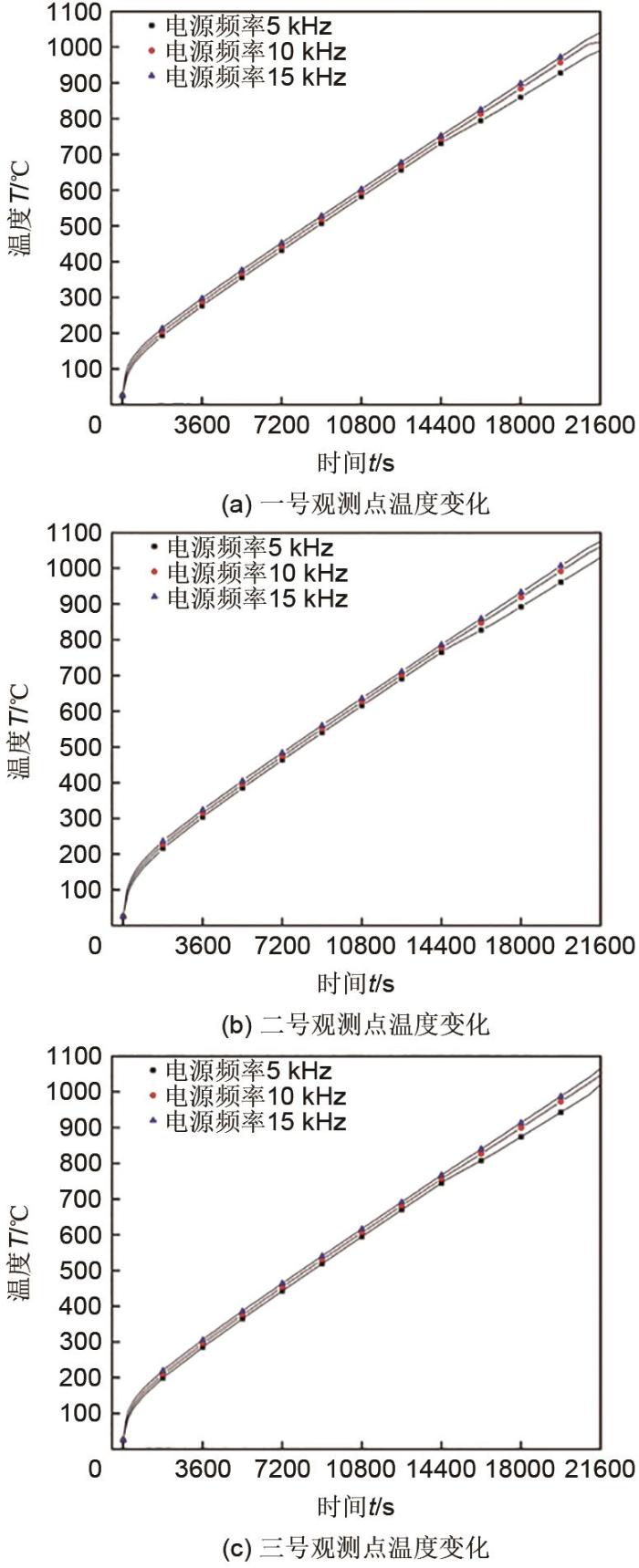
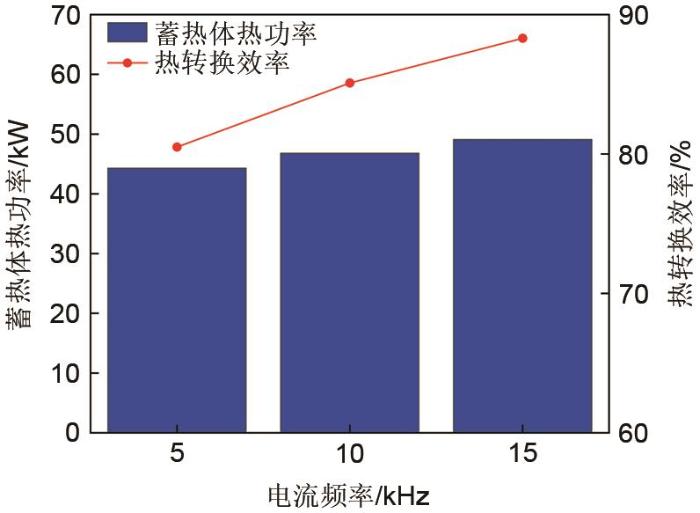
当线圈电流为100 A,电流频率分别为5 kHz、10 kHz、15 kHz时,观测点温度变化如图10所示。从图可看出,电源频率升高,各观测点最高温度均有一定提升。根据图4、图8的感应电流密度可知,感应电流密度越大,蓄热体局部温度越高,当电流频率为5 kHz时,观测点温度分别为990 ℃、1030 ℃、1020 ℃;电流频率为10 kHz时,观测点温度分别为1015 ℃、1066 ℃、1030 ℃;电流频率为15 kHz时,观测点温度分别为1040 ℃、1075 ℃、1065 ℃,3个观测点温度均有一定升高。根据2.4小节可计算出蓄热体吸收热功率与装置热转换效率,经计算可得,电源功率为55 kW,电流频率为5 kHz、10 kHz、15 kHz时,蓄热体吸收热功率分别为44.3 kW、46.7 kW、48.6 kW,装置热转换效率分别为80.5%、84.9%、88.3%,均在80%~90%之间,不同电流频率下蓄热体吸收热功率与装置热转换效率如图11所示。
图10
图10
不同电流频率下观测点温度变化曲线
Fig. 10
Temperature change curves of observation points at different current frequencies
图11
图11
不同电流频率下蓄热体吸收热功率与装置热转换效率
Fig. 11
The heat power absorbed by the heat storage body and the heat conversion efficiency of the device under different current frequencies
3.4 流体流速对温度场分布影响
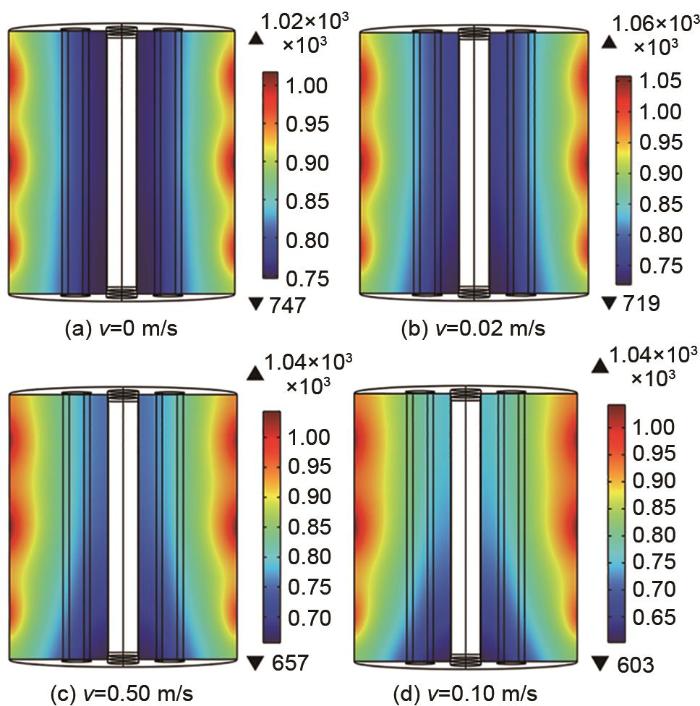
图12
图12
加热6 h时,蓄热体切面温度分布(z=0.75 m)
Fig. 12
Temperature distribution of heat storage body section (z=0.75 m) when heated for 6 h
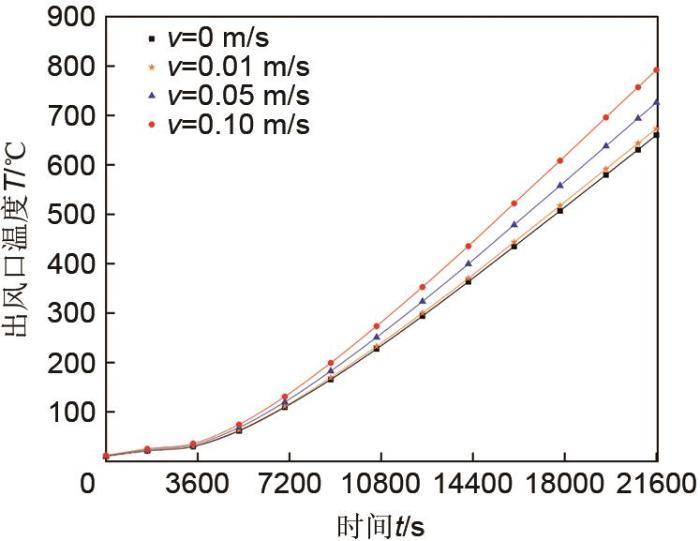
流体流速分别为0 m/s、0.01 m/s、0.05 m/s、0.10 m/s时,蓄热装置出口温度变化曲线如图13所示。由图可知,装置出口温度随流体流速增大而增大,加热6 h后蓄热装置出口温度分别660 ℃、673 ℃、726 ℃、792 ℃。结合图12可以看出,当流体流速为0.02 m/s时,蓄热体最高温度升高40 ℃,整体温度分布较无风速时无明显变化;当流体流速为0.10 m/s时,蓄热体最高温度为1040 ℃,最低温度为603 ℃,相较于流体流速为0.05 m/s时,热量散失较大;当流体流速为0.05 m/s时,蓄热体最高温度为1040 ℃,最低温度为657 ℃,整体温度达到750 ℃以上,同时具有良好的均温性。
图13
图13
不同入口风速下蓄热装置出口温度变化曲线
Fig. 13
Temperature variation curve of heat storage device outlet under different inlet wind speeds
4 结论
本工作以某企业搭建采用感应加热的电热储能实验装置为基础,通过流固耦合的方式搭建其数学模型并模拟其工作状态,研究不同条件对其储热性能的影响,对其蓄热效果进行评估,得出如下结论:
(1)相比电阻加热方式,电磁感应加热速度更快,该技术及时响应未来电力市场中负荷侧的需求。
(2)电流频率的改变只会影响蓄热体表面磁感应强度与感应电流密度大小,并不会影响其在蓄热体表面分布,电流频率增大,蓄热体表面温度升高。
(3)流体流速会影响蓄热体温度分布,增大入口风速可以使温度更有效地向蓄热体内部传递,而风速过大会导致蓄热体热量散失,当风速为0.05 m/s时,蓄热体内部温度分布均匀性最佳。
应用仿真软件对感应加热电热储能装置蓄热过程进行模拟,对比实验数据验证模型准确性,为使用感应加热的固体电热储能装置开发提供一定理论依据,同时放热阶段相关研究将是今后研究的重点。
参考文献