液流电池系统储液罐中电解液的混合损失及导流策略

doi:10.19799/j.cnki.2095-4239.2022.0693

液流电池系统储液罐中电解液的混合损失及导流策略

王志文, 叶强^,

上海交通大学机械与动力工程学院，上海 200240

Investigation of the mixing loss and guiding strategy of the electrolyte flow in the tanks of a redox flow battery system

WANG Zhiwen, YE Qiang^,

School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

通讯作者: 叶强，副教授，研究方向为液流电池和燃料电池，E-mail：qye@sjtu.edu.cn。

收稿日期: 2022-11-24 修回日期: 2022-12-17

基金资助:

国家自然科学基金. 51776120

Received: 2022-11-24 Revised: 2022-12-17

作者简介 About authors

王志文（1998—），男，硕士研究生，研究方向为液流电池模拟研究；。

摘要

在液流电池电堆运行的过程中，储液罐中的电解液的荷电状态并不均匀，其均值与电堆出口流回储液罐的电解液的荷电状态也有差异。处于不同荷电状态的电解液在储液罐内的浓差扩散会造成能量损失。为了定量研究储液罐中不同荷电状态的电解液混合对系统效率的影响，本工作在电解液完全均匀混合与不混合两种极限情况下对电堆的充放电过程进行了模拟研究，进而分析了真实储液罐中的传质过程并将其与完全均匀混合假设下的结果进行比较。最后根据储液罐中传质过程导致的能量损失来源，提出了利用导流结构来优化罐内电解液传质的策略。研究表明：储液罐中不同荷电状态的电解液混合会使得系统的电解液利用率降低、电压效率下降且对电压效率的影响能够达到1%以上；真实储液罐中与传质相关的损失还受到流动死区的影响，死区的存在不但减小了储液罐中实际可以利用的体积还使得局部区域的浓度梯度增大进一步增加了混合损失。合理设计的导流结构能够减小浓度梯度与扩散面积，本工作对某典型储液罐结构做了初步设计，旨在从减小混合损失的角度出发为液流电池储液罐的设计提供思路。

关键词： 混合损失 ; 储液罐 ; 导流策略 ; 系统效率

Abstract

In a running redox flow battery system, the state of charge (SOC) of the electrolyte in the tanks is not uniform and is different from that of the electrolyte in the outlet of the stack. The mixing of electrolyte with different SOC results in energy loss in tanks. Thus, this paper reports a model-based study on the performance of a redox flow battery under the conditions of complete mixing and nonmixing of electrolytes in the tanks in order to quantify the effect of electrolyte mixing in the tanks on the efficiency of the system. The transport of active species in a real tank is also analyzed and compared with that under complete mixing condition. A diversion structure is proposed to optimize the electrolyte flow in the tanks to minimize the mixing loss in the tank. The results show that the mixing of electrolytes with different SOC in the tanks reduces the utilization rate of electrolyte and the voltage efficiency of the redox flow battery system, and the influence on the voltage efficiency may reach more than 1%. The mass transfer correlated energy loss in the real tank is also affected by the dead zone, where the electrolyte is stagnant. The dead zone reduces the available volume in the tank and increases the concentration gradient adjacent to the dead zone; this leads to increased mixing loss. The use of partition contributes to the reduction of concentration gradient and cross-sectional area of diffusion. This paper also creates a preliminary design for a novel tank structure, aiming to provide ideas for the design of tanks from the perspective of reducing mixing loss.

Keywords： mixing loss ; electrolyte tank ; electrolyte guiding strategy ; system efficiency

PDF (3558KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王志文, 叶强. 液流电池系统储液罐中电解液的混合损失及导流策略[J]. 储能科学与技术, 2023, 12(4): 1148-1157

WANG Zhiwen. Investigation of the mixing loss and guiding strategy of the electrolyte flow in the tanks of a redox flow battery system[J]. Energy Storage Science and Technology, 2023, 12(4): 1148-1157

随着化石能源的消耗，人们将更多的目光投向了新能源发电产业，然而以风光为代表的新能源发电设备易受天气与季节影响具有不稳定的特点，因此需要配备相应的储能设施。液流电池因其具有功率与容量解耦的特性，可以进行模块化设计，非常契合当下新能源储能的要求。对于大型储能系统来说，效率是一个非常重要的考虑因素。目前，关于液流电池系统能量效率的分析与建模工作已经可以细分到系统部件局部损失的定量计算，包括旁路电流以及泵功的损失^[1-2]、活性物质跨膜穿透造成的损失^[3]、电极内部的传质损失^[4]以及其他极化损失^[5]、副反应的影响^[6]等。以上研究大多关心电堆内部，事实上储液罐内部的混合损失同样会降低系统效率。对于一个大型的液流电池储能系统，通常是将电解液储存在储液罐内；在运行的过程中电解液被从储液罐中泵入电堆内部在电极上完成反应之后再流回储液罐，然而储液罐内部的电解液与流经电堆发生电化学反应后再流回储液罐内的电解液有着不同的荷电状态，此时不同荷电状态的电解液之间的混合就会产生㶲损从而使得系统效率降低。

在当前液流电池的模型中针对储液罐的处理往往使用均匀搅拌桶模型^[7]，即假设储液罐里面的电解液是实时均匀混合的。而实际上储液罐里面的传质会受到储液罐几何结构的影响，储液罐的结构不仅会影响到储液罐里面的流场分布与其控制的对流传质过程^[8]，还会直接影响到浓度梯度与扩散截面积从而对不同荷电状态的电解液之间的扩散产生影响。储液罐内部不同荷电状态电解液之间的混合并不是均匀搅拌桶模型所假设的完全均匀混合，而是介于完全均匀混合与不混合之间，因此均匀搅拌桶模型与真实储液罐中传质的差异需要进行评估。本工作通过两种理想情况下的电堆供液方式来研究电解液完全均匀混合与不混合两种情况，通过模拟对比了电堆充放电过程中电解液混合与不混合情况下的差异；然后围绕一个典型的储液罐实例讨论了真实储液罐模型中的传质问题及其与均匀搅拌桶模型的差异；最后，从降低储液罐内的死区和不同荷电状态电解液掺混的角度出发，对储液罐内添加导流结构的优化措施进行了研究。

1 系统简化与模型描述

1.1　几何结构与模型假设

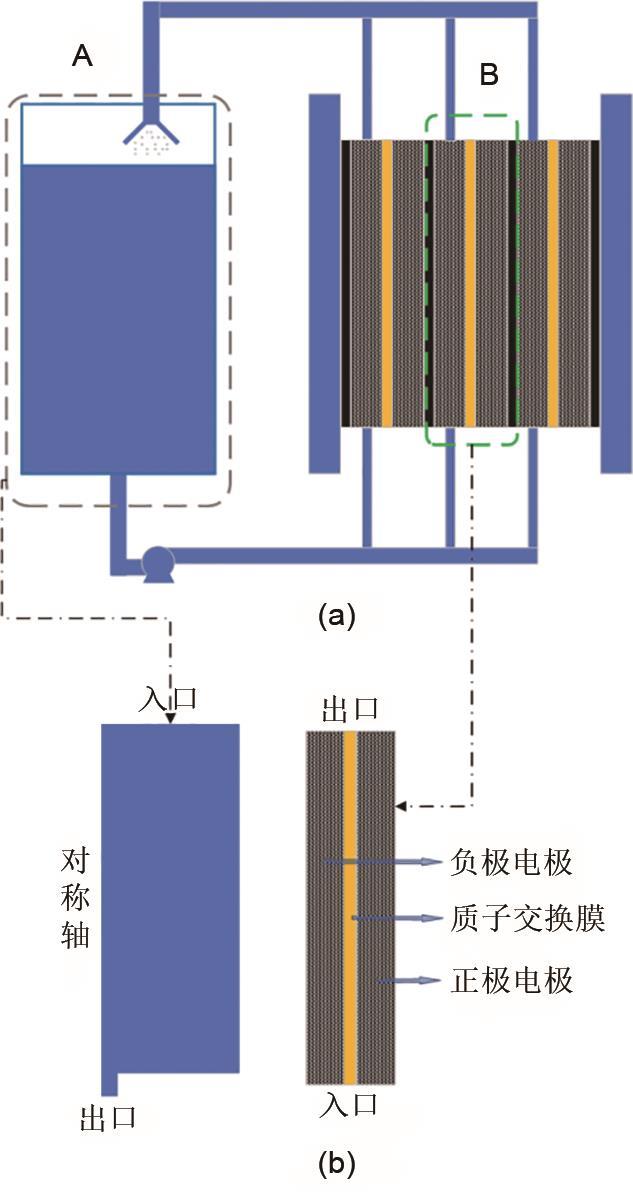
液流电池系统通常包括电堆、管路、储液罐及各种辅助设备，图1(a)为液流电池系统的简化示意图。电堆运行过程中，储液罐中的电解液经由泵泵送到电堆电极中，其中的活性离子在多孔电极中发生氧化还原反应后，再随电解液流回储液罐。本工作以最常见的全钒液流电池系统作为研究实例，其主反应为

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 (a) 电堆与储罐系统示意图; (b) 二维简化模型

Fig. 1 (a) Schematic of the redox flow battery system; (b) Schematic of the simplified 2D models

正极：

V O^{2 +} + H_{2} O V O_{2}^{+} + 2 H^{+} + e^{-}

E_{+}^{0} = 1.004 V v s . S H E

(1)

负极：

V^{3 +} + e^{-} V^{2 +}

E_{-}^{0} = - 0.255 V v s . S H E

(2)

总反应：

V O^{2 +} + H_{2} O + V^{3 +} V O_{2}^{+} + 2 H^{+} + V^{2 +}

V_{c e l l}^{0} = 1.259 V

(3)

为了模拟液流电池系统的非稳态充放电过程，计算模型包括如下简化假设：

（1）储液罐为轴对称的圆柱形、电堆内部各区域的电导率是各向同性的、电极内部电解液仅沿平行于膜的方向向上[图1(b)]流动；

（2）各部分电解液的流动为不可压缩的层流；

（3）不考虑反应的热效应，求解区域内温度恒定；

（4）电解质采用稀溶液假设；

（5）离子交换膜为理想的质子交换膜，仅允许氢离子通过；

（6）忽略析气、沉淀等副反应。

基于上述假设对模型求解区域进行简化：提取图1(a)中的区域A、B作为求解区域，其中储液罐简化为二维轴对称模型，单电池忽略垂直纸面方向的变化简化为二维模型如图1(b)所示。求解区域的几何参数如表1所示。

表1 模型几何参数表

Table 1 Geometric parameters of the models

参数	描述	数值
$H_{e l e}$	电极高度/ $c m$	40
$W_{e l e}$	电极宽度/ $c m$	50
$L_{e l e}$	电极厚度/ $m m$	5
$L_{m e m}$	膜厚度/ $m m$	0.207
$H_{t a n k}^{①}$	储液罐高度/ $m$	6
$R_{t a n k}^{①}$	储液罐半径/ $m$	1.5
$H_{t a n k}^{②}$	储液罐高度/ $m$	3.375
$R_{t a n k}^{②}$	储液罐半径/ $m$	2
$D_{p i p e}$	储液罐出口直径/ $c m$	15
$L_{b a f f}$	导流板厚度/ $c m$	2
$H_{b a f f}$	导流板高度/ $m$	5.8

注：①、②为两种储液罐设计，储罐②相对矮粗仅为与储罐①对比；除特别说明外，本工作涉及研究基于储罐①。

新窗口打开| 下载CSV

1.2　模型控制方程

电解质中各组分的守恒方程由公式(4)描述：

\frac{\partial}{\partial t} (ε c_{i}) + \nabla \cdot \vec{N_{i}} = S_{i}

(4)

\sum_{i} z_{i} c_{i}^{e} = 0

z_{f} c_{f} + \sum_{i} z_{i} c_{i}^{m} = 0

(5)

对于全钒液流电池，组分 $i$ 包括各价态钒离子 $V^{2 +}$ 、 $V^{3 +}$ 、 $V O^{2 +}$ 、 $V O_{2}^{+}$ ，硫酸根离子 $S O_{4}^{2 -}$ ，硫酸氢根离子 $H S O_{4}^{-}$ 和氢离子 $H^{+}$ 。公式(4)中： $c_{i}$ 为电解液组分 $i$ 的物质的量浓度。电极区域与膜区域的电中性方程如公式(5)所示：其中 $z_{f}$ 、 $c_{f}$ 分别为膜中固定带电粒子的电荷数与物质的量浓度； $ε$ 为电极的孔隙率； $S_{i}$ 为组分 $i$ 的源项，活性物质的源项由电化学反应的速率决定，其余离子的源项来源于 $H S O_{4}^{-}$ 的解离反应，基于篇幅不再一一列出； $\vec{N_{i}}$ 为电解液中 $i$ 组分的通量，各组分的通量由能斯特-普朗克方程计算：

\vec{N_{i}} = - D_{i}^{e f f} \nabla c_{i} - z_{i} u_{i} c_{i} F \nabla ϕ_{l} + \vec{u} c_{i}

(6)

其中： $F$ 为法拉第常数， $z_{i}$ 、 $u_{i}$ 、 $D_{i}^{e f f}$ 分别为组分 $i$ 对应的电荷数、迁移率、有效扩散系数； $u_{i}$ 由能斯特-爱因斯坦方程计算， $D_{i}^{e f f}$ 由贝格曼关系式修正：

u_{i} = \frac{D_{i}^{e f f}}{R T}

(7)

D_{i}^{e f f} = ε^{3 / 2} D_{i}

(8)

其中 $R$ 为摩尔气体常数， $D_{i}$ 为组分 $i$ 的扩散系数。电解液电流由离子的定向运动形成，电解液电流根据公式(9)计算：

\vec{j_{l}} = F \sum_{i} z_{i} \vec{N_{i}}

(9)

固相中的电子电流根据欧姆定律计算：

\vec{j_{s}} = - σ_{s} \nabla ϕ_{s}

(10)

其中 $σ_{s}$ 为多孔电极电导率； $ϕ_{s}$ 为固相电位。根据电荷守恒可以将离子输运控制的离子电流、电极中的固相电流与电化学反应的电流联系起来：

\nabla \cdot \vec{j_{l}} = - \nabla \cdot \vec{j_{s}} = i

(11)

式中 $i$ 为反应电流密度，正极的反应电流密度由巴特-福尔摩方程来表示：

i = a F k_{+} {c_{V O^{2 +}}}^{(1 - α_{+})} {c_{V O_{2}^{+}}}^{α_{+}} [e x p (\frac{(1 - α_{+}) F η_{+}}{R T}) - e x p (\frac{- α_{+} F η_{+}}{R T})]

(12)

其中 $a$ 为多孔电极的比表面积； $k_{+}$ 为正极的反应速率常数； $α_{+}$ 为正极氧化还原反应的电荷转移常数，本工作使用的 $α_{+}$ 为0.55，负极的电荷转移常数 $α_{-}$ 为0.45。 $η_{+}$ 为正极的过电势：

η_{+} = ϕ_{s} - ϕ_{l} - E_{+}^{e q}

(13)

其中 $E_{+}^{e q}$ 为正极反应的平衡电位，由能斯特方程计算：

E_{+}^{e q} = E_{+}^{0} + \frac{R T}{F} l n [\frac{a_{V O_{2}^{+}} (a_{H^{+}}^{+})^{2}}{a_{V O^{2 +}}}]

(14)

其中 $a_{i}$ 为组分 $i$ 的活度。为节省篇幅，公式(12)、(13)、(14)仅列出了正极的情况，对于负极也有类似的公式。上文中物性及动力学参数见表2。

表2 电极和电解液物性及动力学参数表

Table 2 Electrolyte、electrode properties and kinetics

参数	描述	数值
$σ_{s}^{e}$	电极电导率/( $S / m$ )	$200$
$σ_{l}^{m}$	膜电导率/( $S / m$ )	$5$
$ε$	电极孔隙率	$0.93$
$a$	电极比表面积/ $m$ ^-1	3.5×10⁴
$D_{V^{2 +}}$	二价钒离子扩散系数/( $m^{2} / s$ )	4×10^-11
$D_{V^{3 +}}$	三价钒离子扩散系数/( $m^{2} / s$ )	4×10^-11
$D_{V O^{2 +}}$	四价钒离子扩散系数/( $m^{2} / s$ )	6.5×10^-11
$D_{V O_{2}^{+}}$	五价钒离子扩散系数/( $m^{2} / s$ )	6.5×10^-11
$D_{H^{+}}$	氢离子扩散系数/( $m^{2} / s$ )	1.55×10^-9
$D_{H S O_{4}^{-}}$	硫酸氢根离子扩散系数/( $m^{2} / s$ )	2.2×10^-10
$D_{S O_{4}^{2 -}}$	硫酸根离子扩散系数/( $m^{2} / s$ )	1.8×10^-10
$k_{+}$	正极反应速率常数/( $m / s$ )	2.5×10^-8
$k_{-}$	负极反应速率常数/( $m / s$ )	7×10^-8

新窗口打开| 下载CSV

1.3　边界条件及初始条件

对于计算区域A对应的二维轴对称储液罐模型，在储液罐顶部的电解液入口处有

\{\begin{array}{l} p = p_{0} \\ c_{i} = c_{i}^{i n} (t) \end{array}

(15)

其中 $p_{0}$ 为给定的入口压力。 $c_{i}^{i n} (t)$ 为随储液罐出口浓度变化，对于处于恒电流运行条件下的电堆，可以近似认为进出储液罐的活性物质浓度与电池的几何尺寸以及工作状态有如下关系：

c_{i}^{i n} (t) = c_{i}^{o u t} (t) \pm \frac{I}{L_{e l e} F} \frac{H_{e l e}}{u_{0}}

c_{i}^{i n} (0) = c_{i}^{0}

(16)

其中 $I$ 为工作电流密度， $H_{e l e}$ 和 $L_{e l e}$ 分别为电池高度和厚度， $u_{0}$ 为电极内电解液流速， $c_{i}^{0}$ 为初始活性物质浓度，负极储液罐中各离子的初始浓度见表3。在储液罐底部的电解液出口处有：

\{\begin{matrix} \int_{0}^{\frac{D_{p i p e}}{2}} 2 ρ r u (r) d r = m_{0} \\ \vec{n} D_{i} \nabla c_{i} = 0 \end{matrix}

(17)

其中 $m_{0}$ 为电解液质量流量。在储液罐壁面处有

\{\begin{array}{l} \vec{u} = 0 \\ \vec{n} D_{i} \nabla c_{i} = 0 \end{array}

(18)

对于计算区域B对应的二维单电池模型，在电极的入口处给定活性物质浓度，在均匀搅拌桶假设下，入口处边界条件如式(19A)所示：

c_{i} = c_{i}^{i n} (t)

(19A)

V_{t a n k} \frac{\partial c_{i}^{i n}}{\partial t} = W_{e l e} (\int_{0}^{L_{e l e}} u_{0} c_{i}^{o u t} d l - \int_{0}^{L_{e l e}} u_{0} c_{i}^{i n} d l)

c_{i}^{i n} (0) = c_{i}^{0}

(19B)

守恒方程式(19B)表示储液罐供给电堆的活性物质浓度的变化速率通过其在电极进出口边界上的通量积分的差值来计算，式中 $V_{t a n k}$ 为储液罐体积， $c_{i}^{0}$ 为初始活性物质浓度，电池正负极各离子的初始浓度见表3。出口处浓度边界条件为零扩散通量：

\vec{n} D_{i} \nabla c_{i} = 0

(20)

电极进出口处以及膜的顶端和底部的电边界条件均为电绝缘：

\vec{n} \cdot \vec{j_{l}^{e}} = \vec{n} \cdot \vec{j_{s}^{e}} = \vec{n} \cdot \vec{j_{l}^{m}} = \vec{n} \cdot \vec{j_{s}^{m}} = 0

(21)

负极电极左侧边界设置为电接地边界条件，正极电极右侧边界设置为恒电流密度边界条件：

ϕ_{s}^{e} = 0

- \vec{n} \cdot \vec{j_{s}^{e}} = I

(22)

$I$ 为工作电流密度，此模型中使用的工作电流密度为 $100 m A / c m^{2}$ 。由于膜中仅允许氢离子通过，所以膜与电极交界面上的电流均由氢离子的输运构成，由通量守恒可以得到：

\vec{n} \vec{N_{H^{+}}^{e}} = \vec{n} \vec{N_{H^{+}}^{m}}

(23)

由于离子交换膜内存在固定的带电粒子，所以膜与电极界面两侧的氢离子有着不同的浓度，这部分浓度差异造成的离子相电位在膜与电极交界处的阶跃由公式(24)计算：

ϕ_{l}^{e} - ϕ_{l}^{m} = \frac{R T}{F} l n (\frac{c_{H^{+}}^{e}}{c_{H^{+}}^{m}})

(24)

其中 $c_{H^{+}}^{e}$ 和 $c_{H^{+}}^{m}$ 分别为电极侧液相电解质中的氢离子浓度和离子交换膜侧的氢离子浓度；本工作假设膜中的固定电荷磺酸根的浓度为 $1990 m o l / m^{3}$ ，因此膜中氢离子的浓度为固定的 $1990 m o l / m^{3}$ 。

表3 求解域中各离子初始浓度

Table 3 Initial species concentrations

参数	描述	数值
$c_{V^{2 +}}^{0, t a n k}$	储罐中二价钒离子初始浓度/( $m o l / m^{3}$ )	1200
$c_{V^{3 +}}^{0, t a n k}$	储罐中三价钒离子初始浓度/( $m o l / m^{3}$ )	300
$c_{H^{+}}^{0, t a n k}$	储罐中氢离子初始浓度/( $m o l / m^{3}$ )	4237.5
$c_{H S {O_{4}}^{-}}^{0, t a n k}$	储罐中硫酸氢根离子初始浓度/( $m o l / m^{3}$ )	2542.5
$c_{S {O_{4}}^{2 -}}^{0, t a n k}$	储罐中硫酸根离子初始浓度/( $m o l / m^{3}$ )	2857.5
$c_{V^{2 +}}^{0, c e l l}$	负极二价钒离子初始浓度/( $m o l / m^{3}$ )	225
$c_{V^{3 +}}^{0, c e l l}$	负极三价钒离子初始浓度/( $m o l / m^{3}$ )	1275
$c_{V O^{2 +}}^{0, c e l l}$	正极四价钒离子初始浓度/( $m o l / m^{3}$ )	1275
$c_{V O_{2}^{+}}^{0, c e l l}$	正极五价钒离子初始浓度/( $m o l / m^{3}$ )	225
$c_{-, H^{+}}^{0, c e l l}$	负极氢离子初始浓度/( $m o l / m^{3}$ )	3628.1
$c_{+, H^{+}}^{0, c e l l}$	正极氢离子初始浓度/( $m o l / m^{3}$ )	4565.6
$c_{-, H S {O_{4}}^{-}}^{0, c e l l}$	负极硫酸氢根离子初始浓度/( $m o l / m^{3}$ )	2176.9
$c_{+, H S {O_{4}}^{-}}^{0, c e l l}$	正极硫酸氢根离子初始浓度/( $m o l / m^{3}$ )	2739.4
$c_{-, S {O_{4}}^{2 -}}^{0, c e l l}$	负极硫酸根离子初始浓度/( $m o l / m^{3}$ )	2863.1
$c_{+, S {O_{4}}^{2 -}}^{0, c e l l}$	正极硫酸根离子初始浓度/( $m o l / m^{3}$ )	2300.6

新窗口打开| 下载CSV

2 结果与分析

2.1　储液罐中的混合效应对系统效率的影响

电堆在运行的过程中通常是将正负电极解液分别储存在两个储液罐内来对电堆的正负电极分别供液，这种供液方式本文称为双罐系统。为了量化储液罐中不同荷电状态电解液掺混带来的影响，本节对比了双罐均匀搅拌桶假设(完全均匀混合)条件下与四罐系统供液(理想不混合)条件下的系统效率。所谓四罐系统是指正负极的每一侧分别设置两个储液罐(为方便描述命名为A、B罐)，在运行的过程中A、B两个储液罐中的电解液循环流动。假设初始条件下电解液全都存储于A罐中且浓度(荷电状态)均匀，在电堆保持恒定的电流与电解液流量运行时，电堆出口处电解液的荷电状态也保持不变，即流入B罐中的电解液的荷电状态相同，当电解液完全从A罐流入B罐后立即切换供液方式将电解液再由B罐经过电堆流回A罐；同样地，流入A罐中的电解液也是处于相同的荷电状态。由于电解液中的混合损失来自于不同荷电状态的电解液的掺混，四罐系统就可以保证罐中电解液的荷电状态与流入储液罐的电解液的荷电状态一致从而避免了混合带来的损失。本工作中，以均匀搅拌桶假设下的双罐系统来表示电解液完全均匀混合、以四罐系统来表示电解液无混合损失的状态。

2.1.1　电解液利用率

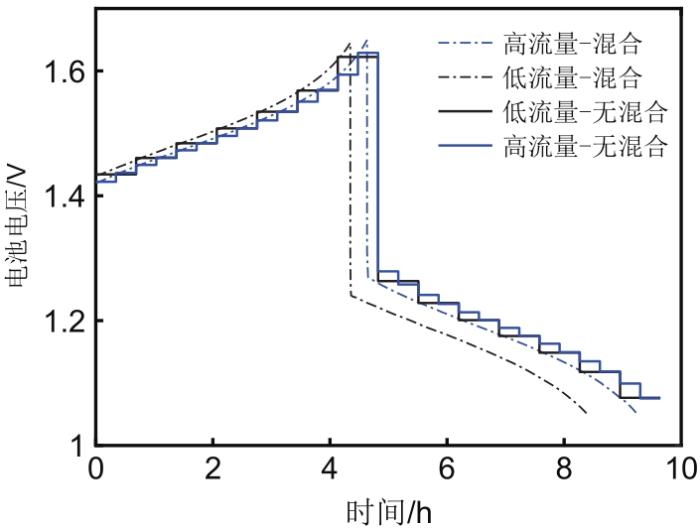
在电堆的运行过程中，为了避免过充或者过放，通常会在固定的电压窗口下运行电堆。图2展示了不同流量下双罐与四罐系统在1.05～1.65 V电压窗口下的充放电电压变化曲线图，初始电解液的荷电状态(SOC)均为0.15。对于充电过程，电解液实时均匀混合的双罐系统在电池电压刚好达到1.65 V时充电停止，而对于电解液不混合的四罐系统则是在电池电压超出截止电压之前结束充电。以低流量工况为例：在第六次切换电解液供应方向之后，电池的充电电压为1.622 V，低于截止电压可以继续充电，但是在下一次切换后电池电压就高于截止电压了，所以在第六次切换供液方式完成循环之后充电截止，此时电池的电压为1.622 V。从图2可以看到，从零时刻到充电截止，四罐系统相较于双罐系统所需的时间更长，即充进了更多的电量；同样如果二者从相同的荷电状态开始放电，四罐系统能够放出更多的电量。对于图2中所示的充放电整个过程，由于四罐系统充入了更多的电量，在充电过程结束时有着更高荷电状态的电解液(以低流量为例：四罐系统SOC=0.924、双罐系统SOC=0.85)，更能够延长其放电过程从而能够输出更多电量。在相同的电压窗口与电解液条件下，四罐系统相较于双罐系统能够在充电阶段充入更多的电量且在放电条件下放出更多的电量，说明了储液罐中电解液的混合损失会降低电解液的利用率。

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 电解液混合不混合条件下定电压窗口充放电电压曲线对比图

Fig. 2 Charge-discharge voltage curves at a fixed voltage window (mixing VS non-mixing)

2.1.2　电压效率

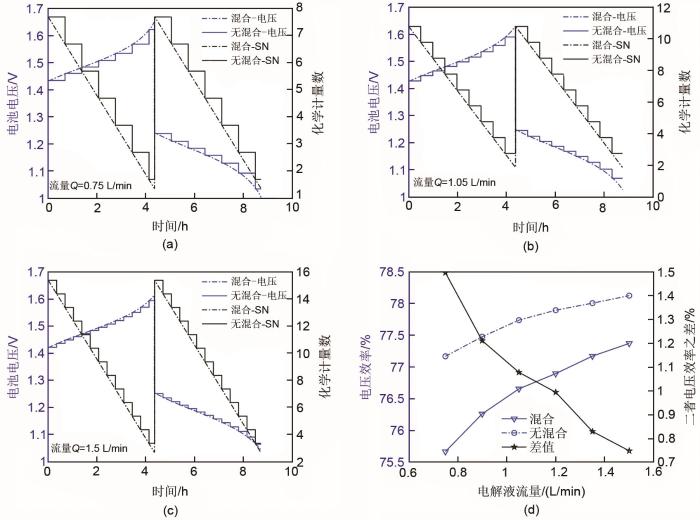
图3展示了固定SOC(0.15～0.85)窗口运行过程中不同电解液流量下的完全均匀混合与无混合状态的电池电压与电堆入口化学计量数(stoichiometric number，SN)的变化。化学计量比的计算公式(25)如下所示：

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 不同恒定流量供液混合与不混合条件下的定SOC窗口充放电电压曲线：(a) 低流量; (b) 中流量; (c) 高流量; (d) 不同电解液流量下混合与不混合的电压效率与其绝对差值

Fig. 3 Charge-discharge voltage curves under mixing and non-mixing conditions at a fixed SOC window using different flow rates: (a) Low flow rate; (b) Middle flow rate; (c) High flow rate; (d) Voltage efficiency and absolute difference between mixing and non-mixing conditions using different flow rates

S N = \frac{n F c_{r} Q}{A I}

(25)

式中 $c_{r}$ 为电解液中反应物的浓度； $Q$ 为电解液流量； $A$ 为电池面积； $n$ 为反应物参与反应过程中要转移的电荷数。本工作中，在充电阶段，反应物为三价和四价钒离子；在放电阶段，反应物为二价和五价钒离子。首先要说明的是，对于不混合条件下的四罐系统运行工况，难以做到一个储液罐中的电解液完全流入另一个储液罐中时电解液的荷电状态恰好达到截止SOC；所以对于四罐系统，当电解液流入罐与电解液流出罐中电解液的平均荷电状态达到截止SOC时充电或放电过程停止。在完全混合条件下储液罐中的电解液是实时均匀混合的，所以电池的电压和化学计量数是连续变化的；相较而言，无混合状态对应的四罐系统，每一侧的电解液储存在两个储液罐中循环流动，当一个罐中的电解液完全流入另一个储液罐后两个储液罐的流入流出关系要进行切换，此时电堆入口的活性物质浓度会发生突变，入口活性物质浓度的突变直接导致了电池电压的突变，这也使得电池电压和入口电解液状态呈现出同步的阶梯形的变化。

与前述固定电压窗口下的充放电过程相同，以图3(a)为例可以发现除了特定节点外在整个充电时段内完全均匀混合状态的充电电压高于无混合状态，而在整个放电过程中则是完全均匀混合状态的放电电压低于无混合状态。在整个充放电的过程中四罐体系的化学计量比始终高于双罐体系，使得无混合状态下的综合电压效率更高。较低的电压效率意味着完全均匀混合状态相较于无混合状态在相同的SOC窗口下需要输入更多的能量反而输出的能量更小，二者在充电或者放电过程中输入和输出的能量之差恰好可以由图3中二者电压曲线围成的面积表示。从二者电压曲线围成的面积我们可以直观地看到随着电解液流量的提升，充放电过程二者输入或输出的能量之差不断减小、两种工况的电压效率也逐渐接近。基于上述变化过程，可以设想当电解液流量进一步提高后二者的差异会进一步减小，极限条件下当电解液流量无限大时：四罐体系的每一次电解液循环时间无限小则图3中的每个阶梯无限小，最终造成二者的电压曲线重合。这意味着在电解液流量较小时通过将双罐体系改为四罐体系，可以有效提升系统电压效率；但当电堆是设计在一个较高的流量运行时，上述供液方式的改造对系统电压效率的提升变得有限，同时高流量工况下还会增加四罐体系中供液方向切换的次数，因此需要何种供液方式需要结合工作电堆的具体设计运行条件而定。事实上，电解液混合造成的损失量大小最直接的影响因素是化学计量比，电解液流量只是影响化学计量比的一个间接因素。图3(d)中展示了不同电解液流量下在定SOC区间充放电时均匀混合与不混合条件下的电压效率与其对应差值。随着电解液流量的提升，混合与不混合条件下电压效率都是逐渐上升而二者的差值则是逐渐减小，与前文推测结果相同；从数值大小上来讲，由混合造成的电压效率的变化幅度在计算的工况范围内可以达到0.7%～1.5%，因此对于大型液流电池储能装置而言，储液罐里面不同荷电状态的电解液的混合造成的损失是一个重要的影响因素。

2.1.3　不同运行条件对混合损失的影响

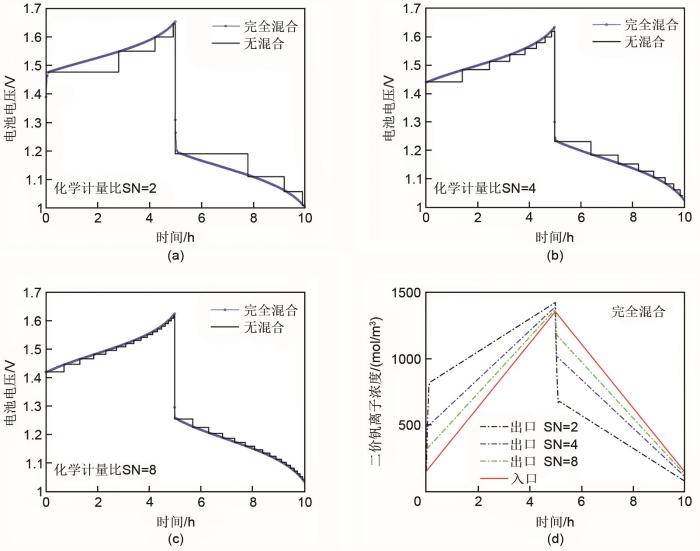
图4(a)、(b)、(c)为恒化学计量比运行下在固定SOC窗口的充放电电压曲线，化学计量比依次为2、4、8。实际运行中恒化学计量比运行的情况不多，本节所展示恒化学计量比运行工况旨在说明造成双罐体系与四罐体系电压效率差异的原因。从化学计量比为2、4、8不同组之间的比较来看，随着化学计量比的提高，四罐与双罐体系运行过程中电压曲线所围成的面积逐渐减小，二者电压效率的差异也逐渐减小。图4(d)展示了三种化学计量比运行条件下的电极进出口的二价钒离子浓度在充放电过程中的变化曲线，虚线代表电极出口处的二价钒离子浓度，实线代表入口处的二价钒离子浓度；电堆在不同化学计量比下运行时活性物质的消耗速率是相同的，因此三者的入口处的钒离子浓度有着相同的变化曲线。从图4(d)中可以发现：随着化学计量比的提升，电极进出口的活性物质浓度的差值逐渐减小。储液罐内部的混合损失来源于储液罐内的电解液的荷电状态与新流入储液罐的电解液的荷电状态的差异，而进出口活性物质的浓度差异越小，处于较高荷电状态的电解液荷电状态降低的幅度也就越小，从而使得混合带来的损失越小，四罐系统与双罐系统的差异也就越小。在2.1.2节的讨论中提到“随着流量的升高，混合造成的损失逐渐下降”，通过本节的研究，我们还可以从化学计量比的角度来解释这一现象。从公式(25)中可以看到在其他参数不变的情况下，电解液流量越高化学计量比就越大，储液罐中的混合损失也就越小。

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 恒定化学计量比供液混合与不混合条件下的充放电电压曲线与电极进出口反应物浓度

Fig. 4 Charge-discharge curves of voltage and V²⁺ concentration at the inlet and outlet of the stack using different stoichiometric ratios

2.2　常规储液罐内的传质问题

2.2.1　储液罐中的死区现象

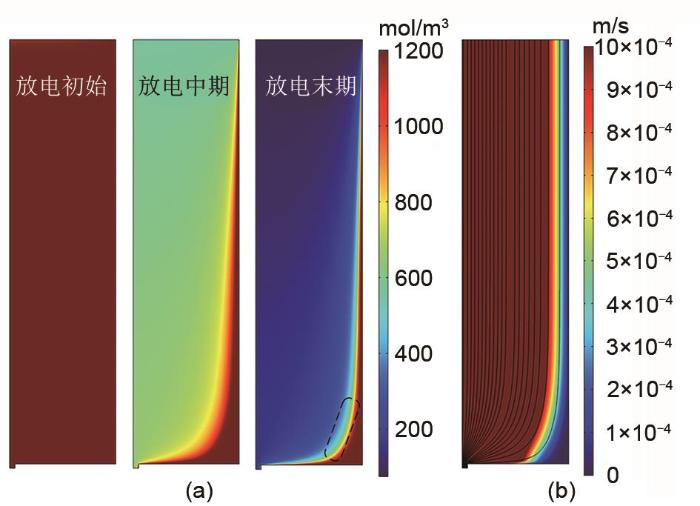
在最常见的双罐液流电池系统中，储液罐内荷电状态不同的电解液既非完全混合也有别于四罐系统的理想不混合，其混合程度与罐内的流场分布密切相关。基于非稳态二维轴对称模型，本工作获得了典型工况下罐内的流场与浓度场分布并着重分析导致能量损失与容量下降的相关传质问题。图5(a)展示了电堆在放电初、中、末期负极储液罐内的二价钒离子浓度的分布。初始阶段储液罐内活性物质二价钒离子的浓度为1200 mol/m³，随着放电过程的进行，储液罐内的电解液被泵送到电堆负极参与反应，随后电解液以更低的荷电状态流回储液罐，因此储液罐内二价钒离子浓度较高的电解液不断被低浓度的电解液驱替使得内部二价钒浓度不断降低。但是储液罐中反应物浓度的降低并不是在内部的每一处同步进行的，而是与电解液在储液罐中存储的空间位置有着密切的联系。放电过程进行到中期时，可以看到罐中大部分区域的电解液浓度已经明显下降且与此时进出口处的浓度差异不大，而在储液罐外周以及底部的小部分区域内二价钒离子的浓度相较于放电初期并没有明显变化，直至放电末期虽然这一现象有所改善，但是有相当一部分区域的电解液没有参与到放电过程，这一部分死区的形成与储液罐的几何形状有着很大的关系。

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 (a) 放电过程不同阶段储液罐内部二价钒离子浓度分布图; (b) 储液罐内流速与流线图

Fig. 5 (a) Distribution of V²⁺ concentration at the beginning、middle and end of discharge; (b) Distribution of velocity and streamline in the tank

图5(b)展示了储液罐内的速度分布与流线。一方面，在靠近储液罐壁面处受壁面无滑移边界的影响电解液流速很低；另一方面，在图1所示的储液罐结构下，电解液只能从储液罐底部中央的出口流出，导致储液罐底部边缘附近的电解液没能被新流入的电解液驱替，最终使得储液罐中形成了死区。储液罐中的传质除流动外还受到浓差驱动下扩散的影响，虽然浓差驱动下的扩散在储液罐内广泛存在，但罐内大部分区域的电解液都处于较低的浓度梯度之下，而从图5(a)可以看到死区的存在创造了一段高浓度梯度的界面；因此死区的存在不但降低了储罐的有效储液空间，还加大了局部区域的浓度梯度，进一步加大了储液罐内的混合损失。从图5(a)放电中期到放电末期的演化过程可以发现死区范围并没有明显改变，说明这种浓差驱动下的扩散相较于流动控制的对流传质的影响是很小的，储液罐中的传质过程主要由对流传质控制。

2.2.2　对电池性能的影响

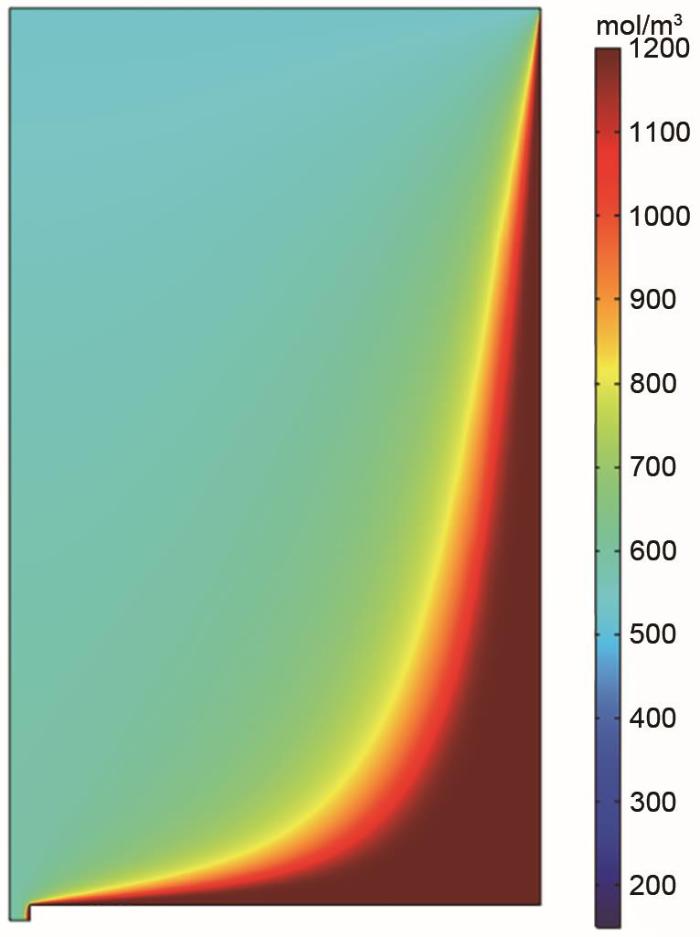
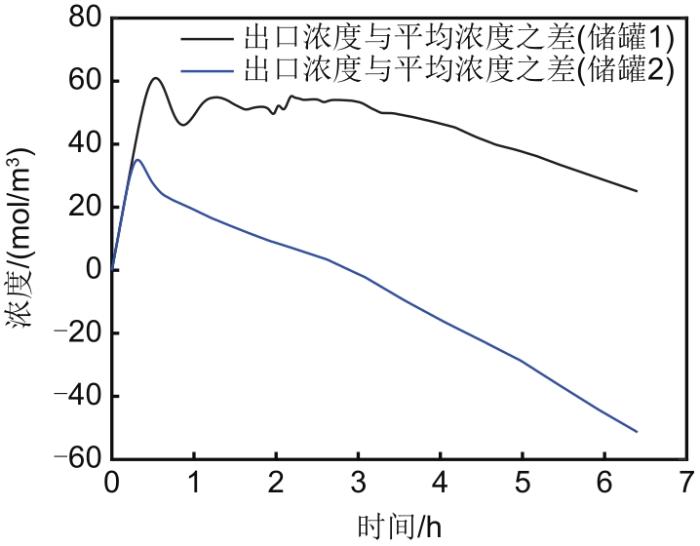
为了进一步说明储液罐中的传质过程对电池性能的影响，我们在保证储罐容量不变的情况下增加储罐直径并同时减小高度得到较为矮粗的储罐2(参数见表1)，基于储罐2的系统我们命名为系统2。图6为系统2在放电中期储罐2内部的二价钒离子浓度分布图。相较于相同放电状态的储罐1，可以发现储罐2中的死区面积更大，这是因为当储液罐变得更加粗短之后流动影响不到的区域有所增大。图7为放电过程中两种储液罐出口处二价钒浓度与平均浓度之差的变化图，需要说明的是，罐内的平均浓度对应于均匀搅拌桶假设下储液罐的出口浓度。在放电开始后的一小段时间内，反应后流回储液罐的荷电状态较低的电解液的影响还没有扩散到储液罐出口处，系统1和系统2的储液罐均保持出口浓度不变，但罐内平均浓度在逐渐下降，所以图7中曲线会先有一段上升；在后续过程中，储液罐出口处的活性物质浓度开始受到入口的影响，且由于死区的存在，使得储液罐出口处浓度的下降速度高于罐内平均浓度的下降速度，最终导致储液罐出口处浓度与罐内平均浓度的差值在经过初始的一段时间之后不断下降。通过图7中的曲线斜率可以发现储罐2下降的速度更快，其原因在于更加粗短的储罐2中有着更大的死区面积，相当于储罐2中实际可用的储液体积小于储罐1，相同条件下储液罐的体积越小，罐内的浓度变化速率越快。另外注意到，储罐1出口处的活性物质浓度与罐内平均浓度的差值始终是大于零的，所以储罐1相较于均匀搅拌桶模型有着更高的电压效率，但是对于储罐2却并非如此。从以上两个不同几何形状的储液罐的对比可知，若在保证储罐容量不变的前提下进一步降低储罐的高度同时增加直径，储液罐出口处二价钒浓度的下降速度会更快并使得在放电阶段的大部分时间内储液罐出口浓度与平均浓度之差是小于零的，届时完全均匀混合假设反而是高估了系统的电压效率。总体来说，理想混合假设下的均匀搅拌桶模型没有考虑到储液罐中的死区问题，同时也高估了储液罐中电解液混合损失的影响；没有考虑死区影响会使其供给电堆的反应物浓度的变化速率小于真实情况，而对电解液利用率以及电压效率的影响则仍需视储罐具体几何参数而定；本工作储罐1为一个典型的储液罐的几何比例，通过均匀混合假设计算时会对其电压效率与电解液利用率产生低估。

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 储罐2在放电中期时内部的二价钒离子浓度分布图

Fig. 6 Distribution of V²⁺concentration at the middle of discharge in tank 2

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 放电过程中储液罐出口反应物浓度与罐内平均浓度之差随时间变化图

Fig. 7 Variation of the difference between V²⁺ concentration at the outlet of the tank and average V²⁺concentration in the tank during discharge

2.3　储液罐结构优化

从2.1和2.2节中我们得知储液罐中的传质问题不仅有不同荷电状态的电解液之间的混合损失还有储液罐自身几何结构带来的死区的问题。较为细长的储液罐有着更好的传质效果，一方面源于其在相同的进出口浓度下有着更低的浓度梯度与更小的扩散截面积，所以电解液的混合损失较小；另一方面细长的结构也减小了电解液流动影响不到的区域，减小了死区的影响。虽然较为细长的储液罐有着更好的表现，但实际中储液罐的高度是有限制的，而通过储液罐内导流结构的设计同样能够达到增长罐内电解液流经长度以及减小电解液流动横截面积的效果。

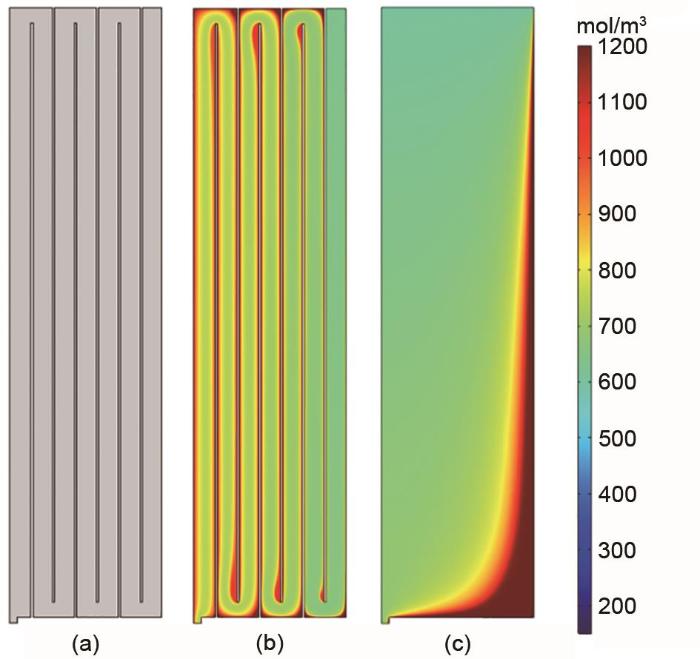
图8(a)为添加了导流板之后的储液罐结构图，运行过程中电解液从右上角入口处进入从左下角流出。相较于传统的储液罐几何结构，大大延长了电解液流动路径、减小了流动的截面积，达到了减小浓度梯度和扩散面积的效果；扩散的量正比于浓度梯度与扩散截面积，所以此导流结构的设计能够大幅减小电解液中活性物质扩散带来的损失。图8(b)为添加了导流板之后的储液罐在系统放电中期时内部的二价钒离子浓度分布，可以看到图8(b)中的死区相较于处于相同放电时期图8(c)中进行结构优化之前的情况有了明显减少，因为导流板的存在能够强迫电解液流过储液罐里的所有区域，这样放电过程中储液罐内的所有区域内的高荷电状态的电解液都会被流回储液罐的较低荷电状态的电解液驱替。恰当的隔板设计来强迫电解液流经储液罐内的每个区域是必要的，这样不仅能减小死区的大小还能减少不同荷电状态电解液之间的掺混，提升了储液罐的有效储液空间，同时又减少了混合损失。

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 (a) 导流结构示意图; (b) 优化后的储液罐处于放电中期时二价钒离子浓度分布图; (c) 初始储液罐处于放电中期时二价钒离子浓度分布图

Fig. 8 (a) Electrolyte guiding structure; (b) Distribution of V²⁺concentration in the tank with electrolyte guiding structure at the middle of discharge; (c) Distribution of V²⁺concentration in the original tank at the middle of discharge

3 结论

本工作通过比较储液罐中电解液完全均匀混合与理想无混合两种极端情况下电堆运行的差异，量化了储液罐中的混合损失对电堆性能的影响；其次基于真实储液罐内流动扩散过程的建模仿真展示了罐内的浓度分布与演化，讨论了当前广泛使用的均匀搅拌桶模型与真实储液罐内传质过程的差异；最后从减小储液罐内混合损失的角度出发提出了储液罐内导流板的设计思路。具体结论分为以下几点：

（1）储液罐中不同荷电状态的电解液混合损失会降低系统输入和输出的电量，减小储液罐内的混合损失有助于提升系统的电解液利用率。

（2）储液罐中的混合损失会降低系统的电压效率，在本工作所研究的电解液流量范围内，电解液完全均匀混合与不混合运行条件下的电压效率之差在0.7%～1.5%，对于大型储能系统来说，储液罐内的混合损失需要引起足够的重视。

（3）造成储液罐内混合损失的根本原因在于储液罐内的电解液与发生反应后再流回储液罐的电解液的荷电状态存在差异，而化学计量比的大小决定了上述二者的差异大小；完全均匀混合与不混合两种极端情况下的差异随着化学计量比的增加而减小，当化学计量比不断增大时二者趋于一致。

（4）均匀搅拌桶模型所作的假设相较于实际储液罐中的传质忽略了死区的问题，但是高估了系统内的混合损失；死区的存在不仅降低了储液罐的实际可供使用的体积，还增加了局部区域的浓度梯度，进一步增大了浓差驱动下的混合损失。

（5）使用较细长的储液罐有助于缓解储液罐内的混合损失，在储液罐内添加恰当的导流结构也能达到同样的效果；除此之外，通过导流结构引导电解液流经储液罐内的所有区域有助于减小储液罐内的死区，提升储液罐容积的有效利用率。

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

YE Q, HU J, CHENG P, et al. Design trade-offs among shunt current, pumping loss and compactness in the piping system of a multi-stack vanadium flow battery[J]. Journal of Power Sources, 2015, 296: 352-364.

[本文引用: 1]

[2]

DELGADO N M, MONTEIRO R, CRUZ J, et al. Shunt currents in vanadium redox flow batteries-a parametric and optimization study[J]. Electrochimica Acta, 2022, 403: doi: 10.1016/j.electacta.2021.139667

[本文引用: 1]

[3]

SUN J W, SHI D Q, ZHONG H X, et al. Investigations on the self-discharge process in vanadium flow battery[J]. Journal of Power Sources, 2015, 294: 562-568.

[本文引用: 1]

[4]

YOU X, YE Q, CHENG P. The dependence of mass transfer coefficient on the electrolyte velocity in carbon felt electrodes: Determination and validation[J]. Journal of the Electrochemical Society, 2017, 164(11): E3386-E3394.

[本文引用: 1]

[5]

SONG Y X, LI X R, YAN C W, et al. Uncovering ionic conductivity impact towards high power vanadium flow battery design and operation[J]. Journal of Power Sources, 2020, 480: doi: 10.1016/j.jpowsour.2020.229141.

[本文引用: 1]

[6]

王瑄, 叶强. 全钒液流电池电堆局部供液不足导致副反应加剧的现象[J]. 储能科学与技术, 2022, 11(5): 1455-1467.

[本文引用: 1]

WANG X, YE Q. The aggravation of side reactions caused by insufficient localized liquid supply in an all-vanadium redox flow battery stack[J]. Energy Storage Science and Technology, 2022, 11(5): 1455-1467.

[本文引用: 1]

[7]

KNEHR K W, AGAR E, DENNISON C R, et al. A transient vanadium flow battery model incorporating vanadium crossover and water transport through the membrane[J]. Journal of the Electrochemical Society, 2012, 159(9): A1446-A1459.

[本文引用: 1]

[8]

WANG Y T, SMITH K C. Numerical investigation of convective transport in redox flow battery tanks: Using baffles to increase utilization[J]. Journal of Energy Storage, 2019, 25: doi: 10.1016/j.est.2019.100840.

[本文引用: 1]

... 随着化石能源的消耗，人们将更多的目光投向了新能源发电产业，然而以风光为代表的新能源发电设备易受天气与季节影响具有不稳定的特点，因此需要配备相应的储能设施.液流电池因其具有功率与容量解耦的特性，可以进行模块化设计，非常契合当下新能源储能的要求.对于大型储能系统来说，效率是一个非常重要的考虑因素.目前，关于液流电池系统能量效率的分析与建模工作已经可以细分到系统部件局部损失的定量计算，包括旁路电流以及泵功的损失^[1-2]、活性物质跨膜穿透造成的损失^[3]、电极内部的传质损失^[4]以及其他极化损失^[5]、副反应的影响^[6]等.以上研究大多关心电堆内部，事实上储液罐内部的混合损失同样会降低系统效率.对于一个大型的液流电池储能系统，通常是将电解液储存在储液罐内；在运行的过程中电解液被从储液罐中泵入电堆内部在电极上完成反应之后再流回储液罐，然而储液罐内部的电解液与流经电堆发生电化学反应后再流回储液罐内的电解液有着不同的荷电状态，此时不同荷电状态的电解液之间的混合就会产生㶲损从而使得系统效率降低. ...

... 在当前液流电池的模型中针对储液罐的处理往往使用均匀搅拌桶模型^[7]，即假设储液罐里面的电解液是实时均匀混合的.而实际上储液罐里面的传质会受到储液罐几何结构的影响，储液罐的结构不仅会影响到储液罐里面的流场分布与其控制的对流传质过程^[8]，还会直接影响到浓度梯度与扩散截面积从而对不同荷电状态的电解液之间的扩散产生影响.储液罐内部不同荷电状态电解液之间的混合并不是均匀搅拌桶模型所假设的完全均匀混合，而是介于完全均匀混合与不混合之间，因此均匀搅拌桶模型与真实储液罐中传质的差异需要进行评估.本工作通过两种理想情况下的电堆供液方式来研究电解液完全均匀混合与不混合两种情况，通过模拟对比了电堆充放电过程中电解液混合与不混合情况下的差异；然后围绕一个典型的储液罐实例讨论了真实储液罐模型中的传质问题及其与均匀搅拌桶模型的差异；最后，从降低储液罐内的死区和不同荷电状态电解液掺混的角度出发，对储液罐内添加导流结构的优化措施进行了研究. ...

〈

〉