图1
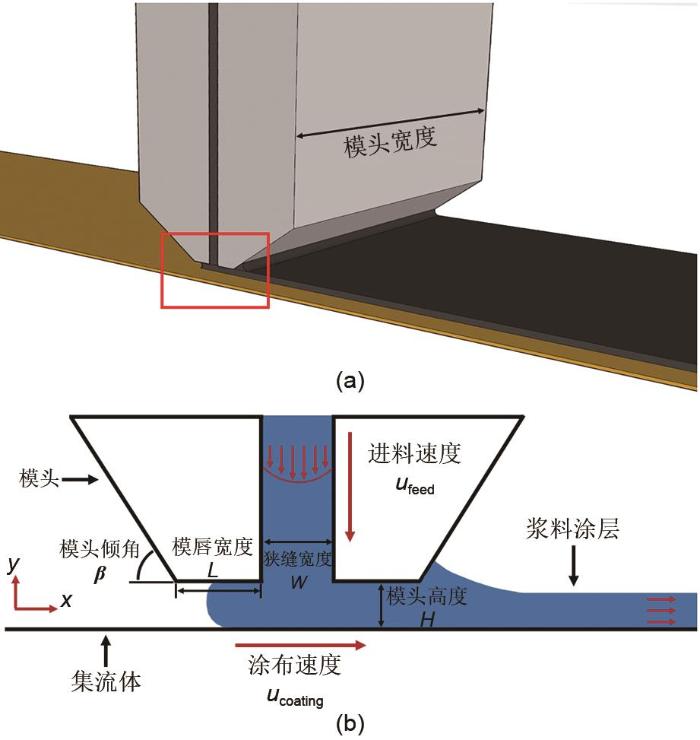
(a) 锂电池电极浆料狭缝涂布示意图;(b) 由涂布模头出口和集流体组成的二维模型示意图
Fig. 1
(a) Schematic diagram of the slit coating of lithium battery electrode slurry ; (b) Schematic diagram of a two-dimensional model composed of the coating die outlet and the current collector
图2
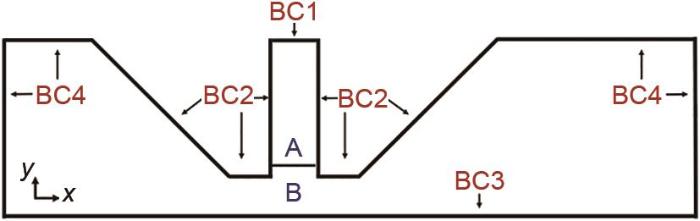
二维模型的计算域和边界
Fig. 2
The computational domain and boundaries of two-dimensional models
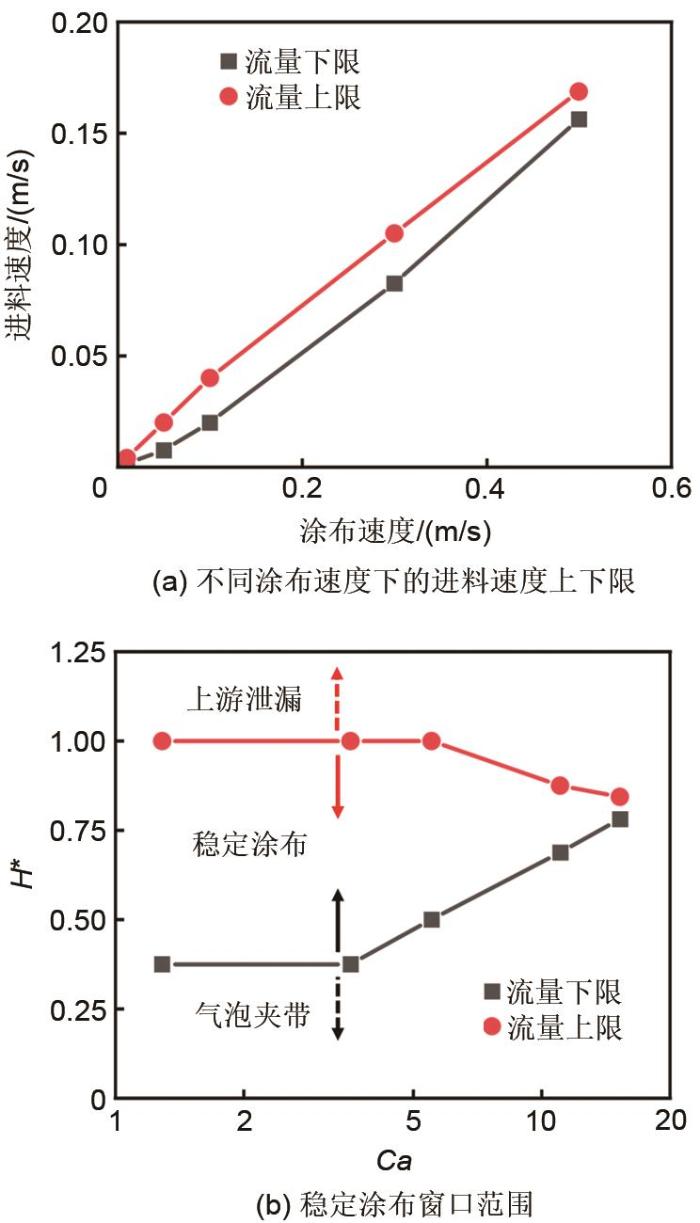
图3
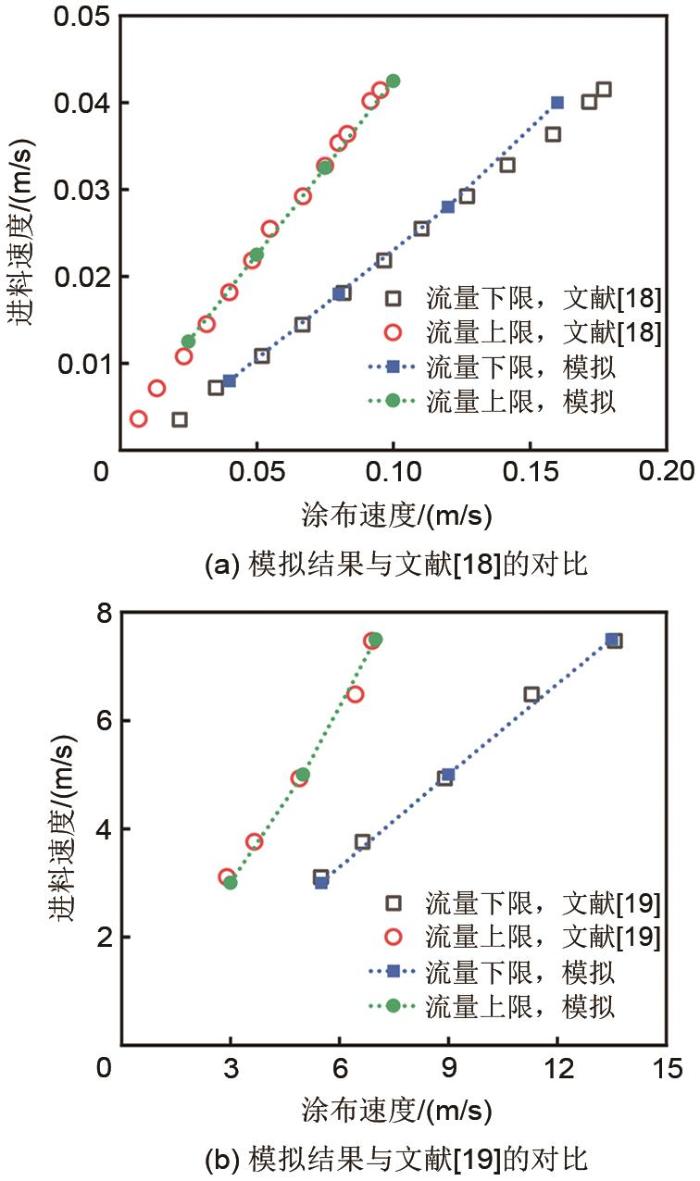
模拟确定的稳定涂布窗口与文献中实验结果的对比
Fig. 3
Comparison of stable coating windows determined through simulation and experiments in literature
图4
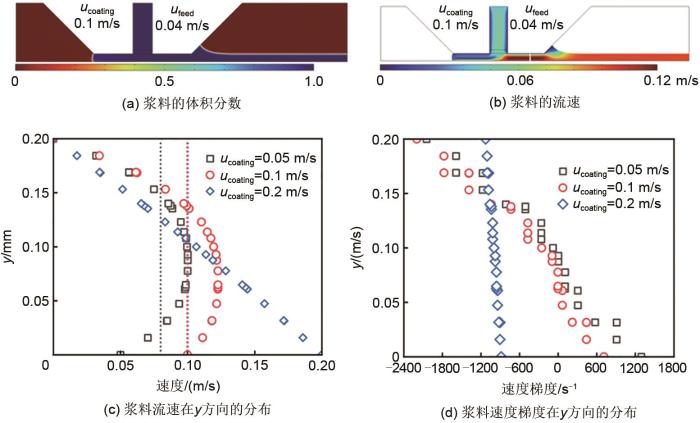
电极浆料的 (a) 体积分数和 (b) 流速的分布,以及 (c) 浆料流速和 (d) 速度梯度在 y
Fig. 4
The distribution of (a) volume fraction and (b) flow rate of electrode slurry, with (c) slurry flow rate and (d) velocity gradient in the y -direction
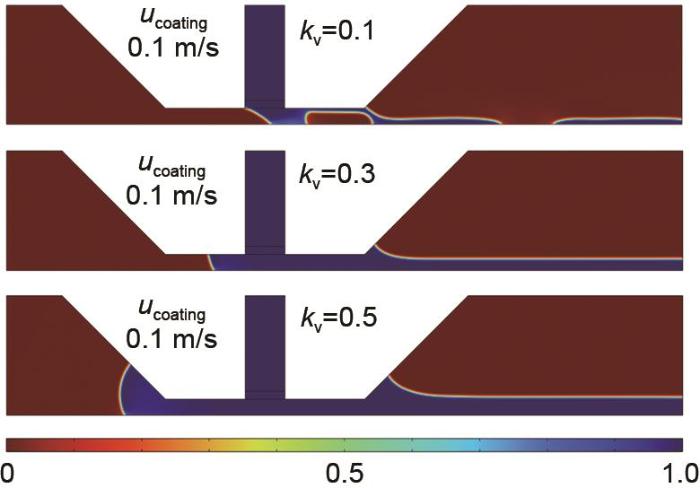
图5
不同进料速度下电极涂层的结构
Fig. 5
Structure of electrode coatings at different feed rates
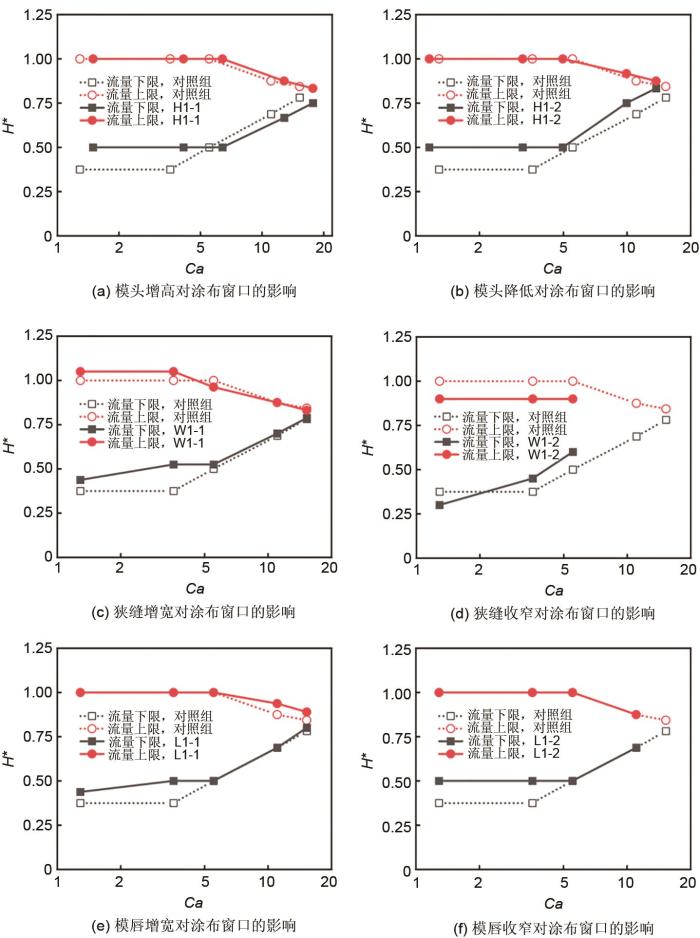
图7
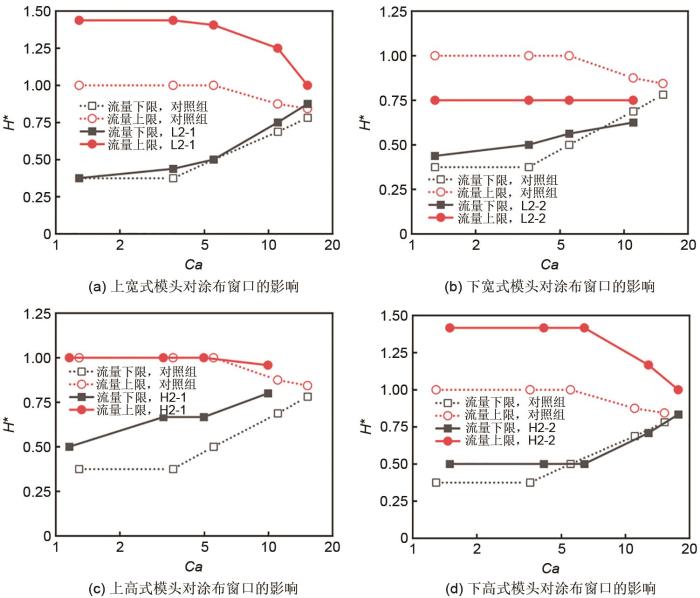
改变涂布模头的主要尺寸对稳定涂布窗口的影响
Fig. 7
The influence of changing the main size of the coating die on the stable coating window
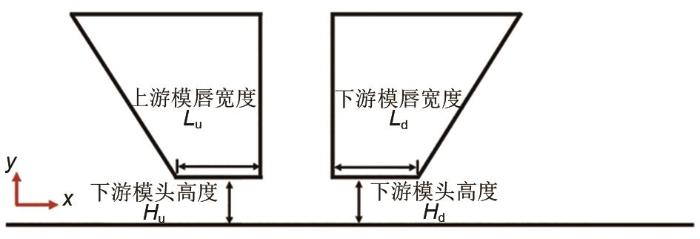
图8
上下游非对称式模头
Fig. 8
Schematic diagram of upstream and downstream asymmetric die heads
图9
采用非对称式模头对稳定涂布窗口的影响
Fig. 9
The influence of asymmetric die heads on stable coating windows
[1]
吴敬华, 杨菁, 刘高瞻, 等. 固态锂电池十年(2011—2021)回顾与展望[J]. 储能科学与技术, 2022, 11(9): 2713-2745.
[本文引用: 1]
WU J H, YANG J, LIU G Z, et al. Review and prospective of solid-state lithium batteries in the past decade(2011—2021)[J]. Energy Storage Science and Technology, 2022, 11(9): 2713-2745.
[本文引用: 1]
[2]
李文俊, 徐航宇, 杨琪, 等. 高能量密度锂电池开发策略[J]. 储能科学与技术, 2020, 9(2): 448-478.
LI W J, XU H Y, YANG Q, et al. Development of strategies for high-energy-density lithium batteries[J]. Energy Storage Science and Technology, 2020, 9(2): 448-478.
[3]
缪平, 姚祯, JOHN Lemmon, 等. 电池储能技术研究进展及展望[J]. 储能科学与技术, 2020, 9(3): 670-678.
MIAO P, YAO Z, JOHN L, et al. Current situations and prospects of energy storage batteries[J]. Energy Storage Science and Technology, 2020, 9(3): 670-678.
[4]
ZHANG X Q, ZHAO C Z, HUANG J Q, et al. Recent advances in energy chemical engineering of next-generation lithium batteries[J]. Engineering, 2018, 4(6): 831-847.
[本文引用: 1]
[5]
郭德超, 郭义敏, 张啟文, 等. 锂离子电池用无溶剂干法电极的制备及其性能研究[J]. 储能科学与技术, 2021, 10(4): 1311-1316.
[本文引用: 1]
GUO D C, GUO Y M, ZHANG Q W, et al. Preparation and characterization of solvent-free dry electrodes for lithium ion batteries[J]. Energy Storage Science and Technology, 2021, 10(4): 1311-1316.
[本文引用: 1]
[6]
梁卫华, 吴大勇, 舒均国. 逗号刮刀涂布流场理论分析与数值模拟[J]. 储能科学与技术, 2021, 10(2): 565-576.
LIANG W H, WU D Y, SHU J G. Theoretical analysis and numerical simulation of flow field in comma scraper coating[J]. Energy Storage Science and Technology, 2021, 10(2): 565-576.
[7]
RYU M, HONG Y K, LEE S Y, et al. Ultrahigh loading dry-process for solvent-free lithium-ion battery electrode fabrication[J]. Nature Communications, 2023, 14: 1316.
[本文引用: 1]
[8]
CHENG P, LIN Y Z, ZAWACKA N K, et al. Comparison of additive amount used in spin-coated and roll-coated organic solar cells[J]. Journal of Materials Chemistry A, 2014, 2(45): 19542-19549.
[本文引用: 2]
[9]
SPIEGEL S, HOFFMANN A, KLEMENS J, et al. Optimization of edge quality in the slot-die coating process of high-capacity lithium-ion battery electrodes[J]. Energy Technology, 2023, 11(5): doi: 10.1002/ente.202200684.
[本文引用: 2]
[10]
闫晓清, 胡志宇, 刘凤泉, 等. 锂离子电池内隔膜褶皱的原因及消除[J]. 储能科学与技术, 2021, 10(1): 156-162.
[本文引用: 1]
YAN X Q, HU Z Y, LIU F Q, et al. Causes and elimination of internal diaphragm wrinkles in lithium ion batteries[J]. Energy Storage Science and Technology, 2021, 10(1): 156-162.
[本文引用: 1]
[11]
谭鹏辉. 锂离子电池极片高效挤压涂布数值模拟及工艺基础[D]. 武汉: 华中科技大学, 2022.
[本文引用: 1]
TAN P H. Numerical simulation and technological basis of efficient extrusion coating of lithium ion battery pole pieces[D]. Wuhan: Huazhong University of Science and Technology, 2022.
[本文引用: 1]
[12]
林黎明. 动力锂电池浆料狭缝式挤压涂布流场数值模拟研究[D]. 郑州: 郑州大学, 2021.
[本文引用: 1]
LIN L M. Numerical simulation of flow field in slit extrusion coating of power lithium battery slurry[D]. Zhengzhou: Zhengzhou University, 2021.
[本文引用: 1]
[13]
AKBARZADEH V, HRYMAK A N. Coupled fluid-particle modeling of a slot die coating system[J]. AIChE Journal, 2016, 62(6): 1933-1939.
[本文引用: 1]
[14]
杜江龙, 林伊婷, 杨雯棋, 等. 模拟仿真在锂离子电池热安全设计中的应用[J]. 储能科学与技术, 2022, 11(3): 866-877.
[本文引用: 1]
DU J L, LIN Y T, YANG W Q, et al. Application of simulation in thermal safety design of lithium-ion batteries[J]. Energy Storage Science and Technology, 2022, 11(3): 866-877.
[本文引用: 1]
[15]
DU J L, TAO H L, CHEN Y X, et al. Thermal management of air-cooling lithium-ion battery pack[J]. Chinese Physics Letters, 2021, 38(11): 122-135.
[16]
HUANG T L, TAN P H, ZHONG Z Y, et al. Numerical and experimental investigation on the defect formation in lithium-ion-battery electrode-slot coating[J]. Chemical Engineering Science, 2022, 258: doi: 10.1016/j.ces.2022.117744.
[本文引用: 1]
[17]
TAN P H, DIAO S M, HUANG T L, et al. Numerical and experimental study on coating uniformity control in simultaneous double-sided slot coating with a novel contacted slot die[J]. Chemical Engineering Science, 2020, 222: doi: 10. 1016/j. ces. 2020. 115716.
[本文引用: 1]
[18]
AHN W G, LEE S H, NAM J, et al. Effect of upstream meniscus shape on dynamic wetting and operating limits of Newtonian coating liquids in slot coating bead flows[J]. Journal of Coatings Technology and Research, 2018, 15(5): 1067-1076.
[本文引用: 2]
[19]
BHAMIDIPATI K L, DIDARI S, BEDELL P, et al. Wetting phenomena during processing of high-viscosity shear-thinning fluid[J]. Journal of Non-Newtonian Fluid Mechanics, 2011, 166(12/13): 723-733.
[本文引用: 2]
[20]
PAN W T, CHEN Z K, CHEN X L, et al. Slot die coating window for a uniform fuel cell ink dispersion[J]. AIChE Journal, 2022, 68(8): e17719.
[本文引用: 1]
[21]
MALAKHOV R, TJIPTOWIDJOJO K, SCHUNK P R. Mechanics of the low-flow limit in slot-die coating with no vacuum[J]. AIChE Journal, 2019, 65(6): e16593.
[本文引用: 1]
1
... 作为新能源领域的代表器件之一,锂离子电池因其高能量密度、长循环寿命和高工作电压等优势被广泛应用于电动汽车、大规模储能等领域[1 -4 ] .随着生产力的快速发展,锂离子电池的需求量与日俱增,如何提高生产效率及良品率成为了近年来的重要议题.极片的制造是锂离子电池生产流程中的核心部分,相对于静电喷涂沉积、辊磨等新工艺,狭缝涂布具有稳定可控、便于大规模生产等优点,仍然是制造锂电池极片的主流工艺[5 -8 ] .然而,当涂布速度过快时电极表面会形成条纹、斑点、波浪等缺陷.缺陷的存在不仅使电池性能降低,严重时还会导致安全事故[9 -10 ] .电极涂层缺陷的成因分为两类,分别为不合理的工艺参数组合以及其他偶然因素.其中,前者造成的缺陷范围更大,可能导致良品率的大幅下降.因此,狭缝涂布工艺参数的组合优化对于提高锂电池产率、降低综合成本有重要意义.在实际工业生产中,涂布机的宽度能够达到1 m以上,通过生产测试对涂布工艺参数进行调整将耗费大量的物料及时间成本[7 ] .采用模拟仿真对电极浆料的狭缝涂布过程进行研究是理想的选择. ...
1
... 作为新能源领域的代表器件之一,锂离子电池因其高能量密度、长循环寿命和高工作电压等优势被广泛应用于电动汽车、大规模储能等领域[1 -4 ] .随着生产力的快速发展,锂离子电池的需求量与日俱增,如何提高生产效率及良品率成为了近年来的重要议题.极片的制造是锂离子电池生产流程中的核心部分,相对于静电喷涂沉积、辊磨等新工艺,狭缝涂布具有稳定可控、便于大规模生产等优点,仍然是制造锂电池极片的主流工艺[5 -8 ] .然而,当涂布速度过快时电极表面会形成条纹、斑点、波浪等缺陷.缺陷的存在不仅使电池性能降低,严重时还会导致安全事故[9 -10 ] .电极涂层缺陷的成因分为两类,分别为不合理的工艺参数组合以及其他偶然因素.其中,前者造成的缺陷范围更大,可能导致良品率的大幅下降.因此,狭缝涂布工艺参数的组合优化对于提高锂电池产率、降低综合成本有重要意义.在实际工业生产中,涂布机的宽度能够达到1 m以上,通过生产测试对涂布工艺参数进行调整将耗费大量的物料及时间成本[7 ] .采用模拟仿真对电极浆料的狭缝涂布过程进行研究是理想的选择. ...
1
... 作为新能源领域的代表器件之一,锂离子电池因其高能量密度、长循环寿命和高工作电压等优势被广泛应用于电动汽车、大规模储能等领域[1 -4 ] .随着生产力的快速发展,锂离子电池的需求量与日俱增,如何提高生产效率及良品率成为了近年来的重要议题.极片的制造是锂离子电池生产流程中的核心部分,相对于静电喷涂沉积、辊磨等新工艺,狭缝涂布具有稳定可控、便于大规模生产等优点,仍然是制造锂电池极片的主流工艺[5 -8 ] .然而,当涂布速度过快时电极表面会形成条纹、斑点、波浪等缺陷.缺陷的存在不仅使电池性能降低,严重时还会导致安全事故[9 -10 ] .电极涂层缺陷的成因分为两类,分别为不合理的工艺参数组合以及其他偶然因素.其中,前者造成的缺陷范围更大,可能导致良品率的大幅下降.因此,狭缝涂布工艺参数的组合优化对于提高锂电池产率、降低综合成本有重要意义.在实际工业生产中,涂布机的宽度能够达到1 m以上,通过生产测试对涂布工艺参数进行调整将耗费大量的物料及时间成本[7 ] .采用模拟仿真对电极浆料的狭缝涂布过程进行研究是理想的选择. ...
1
... 作为新能源领域的代表器件之一,锂离子电池因其高能量密度、长循环寿命和高工作电压等优势被广泛应用于电动汽车、大规模储能等领域[1 -4 ] .随着生产力的快速发展,锂离子电池的需求量与日俱增,如何提高生产效率及良品率成为了近年来的重要议题.极片的制造是锂离子电池生产流程中的核心部分,相对于静电喷涂沉积、辊磨等新工艺,狭缝涂布具有稳定可控、便于大规模生产等优点,仍然是制造锂电池极片的主流工艺[5 -8 ] .然而,当涂布速度过快时电极表面会形成条纹、斑点、波浪等缺陷.缺陷的存在不仅使电池性能降低,严重时还会导致安全事故[9 -10 ] .电极涂层缺陷的成因分为两类,分别为不合理的工艺参数组合以及其他偶然因素.其中,前者造成的缺陷范围更大,可能导致良品率的大幅下降.因此,狭缝涂布工艺参数的组合优化对于提高锂电池产率、降低综合成本有重要意义.在实际工业生产中,涂布机的宽度能够达到1 m以上,通过生产测试对涂布工艺参数进行调整将耗费大量的物料及时间成本[7 ] .采用模拟仿真对电极浆料的狭缝涂布过程进行研究是理想的选择. ...
1
... 作为新能源领域的代表器件之一,锂离子电池因其高能量密度、长循环寿命和高工作电压等优势被广泛应用于电动汽车、大规模储能等领域[1 -4 ] .随着生产力的快速发展,锂离子电池的需求量与日俱增,如何提高生产效率及良品率成为了近年来的重要议题.极片的制造是锂离子电池生产流程中的核心部分,相对于静电喷涂沉积、辊磨等新工艺,狭缝涂布具有稳定可控、便于大规模生产等优点,仍然是制造锂电池极片的主流工艺[5 -8 ] .然而,当涂布速度过快时电极表面会形成条纹、斑点、波浪等缺陷.缺陷的存在不仅使电池性能降低,严重时还会导致安全事故[9 -10 ] .电极涂层缺陷的成因分为两类,分别为不合理的工艺参数组合以及其他偶然因素.其中,前者造成的缺陷范围更大,可能导致良品率的大幅下降.因此,狭缝涂布工艺参数的组合优化对于提高锂电池产率、降低综合成本有重要意义.在实际工业生产中,涂布机的宽度能够达到1 m以上,通过生产测试对涂布工艺参数进行调整将耗费大量的物料及时间成本[7 ] .采用模拟仿真对电极浆料的狭缝涂布过程进行研究是理想的选择. ...
1
... 作为新能源领域的代表器件之一,锂离子电池因其高能量密度、长循环寿命和高工作电压等优势被广泛应用于电动汽车、大规模储能等领域[1 -4 ] .随着生产力的快速发展,锂离子电池的需求量与日俱增,如何提高生产效率及良品率成为了近年来的重要议题.极片的制造是锂离子电池生产流程中的核心部分,相对于静电喷涂沉积、辊磨等新工艺,狭缝涂布具有稳定可控、便于大规模生产等优点,仍然是制造锂电池极片的主流工艺[5 -8 ] .然而,当涂布速度过快时电极表面会形成条纹、斑点、波浪等缺陷.缺陷的存在不仅使电池性能降低,严重时还会导致安全事故[9 -10 ] .电极涂层缺陷的成因分为两类,分别为不合理的工艺参数组合以及其他偶然因素.其中,前者造成的缺陷范围更大,可能导致良品率的大幅下降.因此,狭缝涂布工艺参数的组合优化对于提高锂电池产率、降低综合成本有重要意义.在实际工业生产中,涂布机的宽度能够达到1 m以上,通过生产测试对涂布工艺参数进行调整将耗费大量的物料及时间成本[7 ] .采用模拟仿真对电极浆料的狭缝涂布过程进行研究是理想的选择. ...
2
... 作为新能源领域的代表器件之一,锂离子电池因其高能量密度、长循环寿命和高工作电压等优势被广泛应用于电动汽车、大规模储能等领域[1 -4 ] .随着生产力的快速发展,锂离子电池的需求量与日俱增,如何提高生产效率及良品率成为了近年来的重要议题.极片的制造是锂离子电池生产流程中的核心部分,相对于静电喷涂沉积、辊磨等新工艺,狭缝涂布具有稳定可控、便于大规模生产等优点,仍然是制造锂电池极片的主流工艺[5 -8 ] .然而,当涂布速度过快时电极表面会形成条纹、斑点、波浪等缺陷.缺陷的存在不仅使电池性能降低,严重时还会导致安全事故[9 -10 ] .电极涂层缺陷的成因分为两类,分别为不合理的工艺参数组合以及其他偶然因素.其中,前者造成的缺陷范围更大,可能导致良品率的大幅下降.因此,狭缝涂布工艺参数的组合优化对于提高锂电池产率、降低综合成本有重要意义.在实际工业生产中,涂布机的宽度能够达到1 m以上,通过生产测试对涂布工艺参数进行调整将耗费大量的物料及时间成本[7 ] .采用模拟仿真对电极浆料的狭缝涂布过程进行研究是理想的选择. ...
... 根据文献[8 -9 ]中的实验工况,采用二维模型进行有限元模拟.模拟中所采用的控制方程、边界条件以及空气的物性参数均与上文中一致,模型的几何尺寸及浆料的物性参数的设置与文献一致:在与Ahn等[18 ] 的实验结果进行对比时,狭缝宽度、模头高度、表面张力均与本工作所采用的一致,浆料为μ l =0.045 Pa∙ s的牛顿流体,浆料与模头、集流体之间的接触角均为60°;在与Bhamidipati等[19 ] 的实验结果进行对比时,狭缝宽度为0.25 mm,模头高度为0.25 mm,浆料的流体一致性系数为8.07 Pa∙ s,流动特性指数为0.83,表面张力为0.047 N/m,浆料与模头、集流体之间的接触角分别为69°和62°.稳定涂布窗口即为每个涂布速度所对应的使涂布稳定进行的进料速度的范围,具体的判定标准在下文详细叙述.通过模拟结果与文献中实验结果确定的稳定涂布窗口如图3 所示,本文中的模型展现出较高的准确性和通用性. ...
2
... 作为新能源领域的代表器件之一,锂离子电池因其高能量密度、长循环寿命和高工作电压等优势被广泛应用于电动汽车、大规模储能等领域[1 -4 ] .随着生产力的快速发展,锂离子电池的需求量与日俱增,如何提高生产效率及良品率成为了近年来的重要议题.极片的制造是锂离子电池生产流程中的核心部分,相对于静电喷涂沉积、辊磨等新工艺,狭缝涂布具有稳定可控、便于大规模生产等优点,仍然是制造锂电池极片的主流工艺[5 -8 ] .然而,当涂布速度过快时电极表面会形成条纹、斑点、波浪等缺陷.缺陷的存在不仅使电池性能降低,严重时还会导致安全事故[9 -10 ] .电极涂层缺陷的成因分为两类,分别为不合理的工艺参数组合以及其他偶然因素.其中,前者造成的缺陷范围更大,可能导致良品率的大幅下降.因此,狭缝涂布工艺参数的组合优化对于提高锂电池产率、降低综合成本有重要意义.在实际工业生产中,涂布机的宽度能够达到1 m以上,通过生产测试对涂布工艺参数进行调整将耗费大量的物料及时间成本[7 ] .采用模拟仿真对电极浆料的狭缝涂布过程进行研究是理想的选择. ...
... 根据文献[8 -9 ]中的实验工况,采用二维模型进行有限元模拟.模拟中所采用的控制方程、边界条件以及空气的物性参数均与上文中一致,模型的几何尺寸及浆料的物性参数的设置与文献一致:在与Ahn等[18 ] 的实验结果进行对比时,狭缝宽度、模头高度、表面张力均与本工作所采用的一致,浆料为μ l =0.045 Pa∙ s的牛顿流体,浆料与模头、集流体之间的接触角均为60°;在与Bhamidipati等[19 ] 的实验结果进行对比时,狭缝宽度为0.25 mm,模头高度为0.25 mm,浆料的流体一致性系数为8.07 Pa∙ s,流动特性指数为0.83,表面张力为0.047 N/m,浆料与模头、集流体之间的接触角分别为69°和62°.稳定涂布窗口即为每个涂布速度所对应的使涂布稳定进行的进料速度的范围,具体的判定标准在下文详细叙述.通过模拟结果与文献中实验结果确定的稳定涂布窗口如图3 所示,本文中的模型展现出较高的准确性和通用性. ...
1
... 作为新能源领域的代表器件之一,锂离子电池因其高能量密度、长循环寿命和高工作电压等优势被广泛应用于电动汽车、大规模储能等领域[1 -4 ] .随着生产力的快速发展,锂离子电池的需求量与日俱增,如何提高生产效率及良品率成为了近年来的重要议题.极片的制造是锂离子电池生产流程中的核心部分,相对于静电喷涂沉积、辊磨等新工艺,狭缝涂布具有稳定可控、便于大规模生产等优点,仍然是制造锂电池极片的主流工艺[5 -8 ] .然而,当涂布速度过快时电极表面会形成条纹、斑点、波浪等缺陷.缺陷的存在不仅使电池性能降低,严重时还会导致安全事故[9 -10 ] .电极涂层缺陷的成因分为两类,分别为不合理的工艺参数组合以及其他偶然因素.其中,前者造成的缺陷范围更大,可能导致良品率的大幅下降.因此,狭缝涂布工艺参数的组合优化对于提高锂电池产率、降低综合成本有重要意义.在实际工业生产中,涂布机的宽度能够达到1 m以上,通过生产测试对涂布工艺参数进行调整将耗费大量的物料及时间成本[7 ] .采用模拟仿真对电极浆料的狭缝涂布过程进行研究是理想的选择. ...
1
... 作为新能源领域的代表器件之一,锂离子电池因其高能量密度、长循环寿命和高工作电压等优势被广泛应用于电动汽车、大规模储能等领域[1 -4 ] .随着生产力的快速发展,锂离子电池的需求量与日俱增,如何提高生产效率及良品率成为了近年来的重要议题.极片的制造是锂离子电池生产流程中的核心部分,相对于静电喷涂沉积、辊磨等新工艺,狭缝涂布具有稳定可控、便于大规模生产等优点,仍然是制造锂电池极片的主流工艺[5 -8 ] .然而,当涂布速度过快时电极表面会形成条纹、斑点、波浪等缺陷.缺陷的存在不仅使电池性能降低,严重时还会导致安全事故[9 -10 ] .电极涂层缺陷的成因分为两类,分别为不合理的工艺参数组合以及其他偶然因素.其中,前者造成的缺陷范围更大,可能导致良品率的大幅下降.因此,狭缝涂布工艺参数的组合优化对于提高锂电池产率、降低综合成本有重要意义.在实际工业生产中,涂布机的宽度能够达到1 m以上,通过生产测试对涂布工艺参数进行调整将耗费大量的物料及时间成本[7 ] .采用模拟仿真对电极浆料的狭缝涂布过程进行研究是理想的选择. ...
1
... 狭缝涂布过程主要分为两个阶段,电极浆料首先经由外部管道和模头内部流道输送至出口处,然后与集流体发生接触,流经模唇并在模头外部的开放空间中自由流动形成电极涂层.对于模头内部流道的研究通常以提高浆料流动的均匀性为目标,目前已有较多研究[11 -12 ] .电极浆料与集流体接触后,首先在滚动的集流体和固定的模头之间形成剪切流,随后离开模头自由流动,这一过程直接决定了电极涂层的结构.因此,本文假设浆料在到达模头出口附近时稳定流动,研究后续的电极涂层形成过程.Akbarzadeh等[13 ] 研究了电极颗粒、浆料溶剂以及模头边界之间的相互作用,结果表明在涂布过程中电极颗粒的移动路线与浆料的流线高度重叠,并且在低流速区域内相互吸引产生团聚,导致电极颗粒分布得不均匀.因此,流体的流动情况可以体现电极颗粒的行为,保证强度适中的流动是形成稳定涂层的关键.相对于显式粒子模型,将颗粒与溶剂视为整体流体的连续介质模型能够在体现流体主要行为的同时大幅降低计算成本[14 -17 ] .Ahn等[18 ] 和Bhamidipati等[19 ] 分别采用牛顿流体和剪切稀化的非牛顿流体进行了狭缝涂布的实验,并采用相场-流场耦合的模型进行了数值模拟,模拟结果与实验高度一致,表明此类模型具有良好的可靠性.Pan等[20 ] 模拟了电极浆料的狭缝涂布过程,分析了上游模头区域、下游模头区域、自由流动区域中电极浆料流动类型的差异,提出了泊肃叶流-库埃特流-气泡流(Poiseuille-Couette-bubbly flow)的流型转化机制,为寻找稳定涂布窗口提供了理论依据.Malakhov等[21 ] 将涂布速度、黏度、表面张力、模头高度以及涂层膜厚进行了无量纲化,构建了低流量限制模型,预测了在特定浆料性质和模头形状下能够实现的最小无缺陷膜厚,与实验结果对比验证了其有效性.在上述研究中,没有对模头主要尺寸与稳定涂布窗口之间的关联进行系统性分析,研究结果难以直接为工业生产中涂布工艺参数优化提供借鉴. ...
1
... 狭缝涂布过程主要分为两个阶段,电极浆料首先经由外部管道和模头内部流道输送至出口处,然后与集流体发生接触,流经模唇并在模头外部的开放空间中自由流动形成电极涂层.对于模头内部流道的研究通常以提高浆料流动的均匀性为目标,目前已有较多研究[11 -12 ] .电极浆料与集流体接触后,首先在滚动的集流体和固定的模头之间形成剪切流,随后离开模头自由流动,这一过程直接决定了电极涂层的结构.因此,本文假设浆料在到达模头出口附近时稳定流动,研究后续的电极涂层形成过程.Akbarzadeh等[13 ] 研究了电极颗粒、浆料溶剂以及模头边界之间的相互作用,结果表明在涂布过程中电极颗粒的移动路线与浆料的流线高度重叠,并且在低流速区域内相互吸引产生团聚,导致电极颗粒分布得不均匀.因此,流体的流动情况可以体现电极颗粒的行为,保证强度适中的流动是形成稳定涂层的关键.相对于显式粒子模型,将颗粒与溶剂视为整体流体的连续介质模型能够在体现流体主要行为的同时大幅降低计算成本[14 -17 ] .Ahn等[18 ] 和Bhamidipati等[19 ] 分别采用牛顿流体和剪切稀化的非牛顿流体进行了狭缝涂布的实验,并采用相场-流场耦合的模型进行了数值模拟,模拟结果与实验高度一致,表明此类模型具有良好的可靠性.Pan等[20 ] 模拟了电极浆料的狭缝涂布过程,分析了上游模头区域、下游模头区域、自由流动区域中电极浆料流动类型的差异,提出了泊肃叶流-库埃特流-气泡流(Poiseuille-Couette-bubbly flow)的流型转化机制,为寻找稳定涂布窗口提供了理论依据.Malakhov等[21 ] 将涂布速度、黏度、表面张力、模头高度以及涂层膜厚进行了无量纲化,构建了低流量限制模型,预测了在特定浆料性质和模头形状下能够实现的最小无缺陷膜厚,与实验结果对比验证了其有效性.在上述研究中,没有对模头主要尺寸与稳定涂布窗口之间的关联进行系统性分析,研究结果难以直接为工业生产中涂布工艺参数优化提供借鉴. ...
1
... 狭缝涂布过程主要分为两个阶段,电极浆料首先经由外部管道和模头内部流道输送至出口处,然后与集流体发生接触,流经模唇并在模头外部的开放空间中自由流动形成电极涂层.对于模头内部流道的研究通常以提高浆料流动的均匀性为目标,目前已有较多研究[11 -12 ] .电极浆料与集流体接触后,首先在滚动的集流体和固定的模头之间形成剪切流,随后离开模头自由流动,这一过程直接决定了电极涂层的结构.因此,本文假设浆料在到达模头出口附近时稳定流动,研究后续的电极涂层形成过程.Akbarzadeh等[13 ] 研究了电极颗粒、浆料溶剂以及模头边界之间的相互作用,结果表明在涂布过程中电极颗粒的移动路线与浆料的流线高度重叠,并且在低流速区域内相互吸引产生团聚,导致电极颗粒分布得不均匀.因此,流体的流动情况可以体现电极颗粒的行为,保证强度适中的流动是形成稳定涂层的关键.相对于显式粒子模型,将颗粒与溶剂视为整体流体的连续介质模型能够在体现流体主要行为的同时大幅降低计算成本[14 -17 ] .Ahn等[18 ] 和Bhamidipati等[19 ] 分别采用牛顿流体和剪切稀化的非牛顿流体进行了狭缝涂布的实验,并采用相场-流场耦合的模型进行了数值模拟,模拟结果与实验高度一致,表明此类模型具有良好的可靠性.Pan等[20 ] 模拟了电极浆料的狭缝涂布过程,分析了上游模头区域、下游模头区域、自由流动区域中电极浆料流动类型的差异,提出了泊肃叶流-库埃特流-气泡流(Poiseuille-Couette-bubbly flow)的流型转化机制,为寻找稳定涂布窗口提供了理论依据.Malakhov等[21 ] 将涂布速度、黏度、表面张力、模头高度以及涂层膜厚进行了无量纲化,构建了低流量限制模型,预测了在特定浆料性质和模头形状下能够实现的最小无缺陷膜厚,与实验结果对比验证了其有效性.在上述研究中,没有对模头主要尺寸与稳定涂布窗口之间的关联进行系统性分析,研究结果难以直接为工业生产中涂布工艺参数优化提供借鉴. ...
1
... 狭缝涂布过程主要分为两个阶段,电极浆料首先经由外部管道和模头内部流道输送至出口处,然后与集流体发生接触,流经模唇并在模头外部的开放空间中自由流动形成电极涂层.对于模头内部流道的研究通常以提高浆料流动的均匀性为目标,目前已有较多研究[11 -12 ] .电极浆料与集流体接触后,首先在滚动的集流体和固定的模头之间形成剪切流,随后离开模头自由流动,这一过程直接决定了电极涂层的结构.因此,本文假设浆料在到达模头出口附近时稳定流动,研究后续的电极涂层形成过程.Akbarzadeh等[13 ] 研究了电极颗粒、浆料溶剂以及模头边界之间的相互作用,结果表明在涂布过程中电极颗粒的移动路线与浆料的流线高度重叠,并且在低流速区域内相互吸引产生团聚,导致电极颗粒分布得不均匀.因此,流体的流动情况可以体现电极颗粒的行为,保证强度适中的流动是形成稳定涂层的关键.相对于显式粒子模型,将颗粒与溶剂视为整体流体的连续介质模型能够在体现流体主要行为的同时大幅降低计算成本[14 -17 ] .Ahn等[18 ] 和Bhamidipati等[19 ] 分别采用牛顿流体和剪切稀化的非牛顿流体进行了狭缝涂布的实验,并采用相场-流场耦合的模型进行了数值模拟,模拟结果与实验高度一致,表明此类模型具有良好的可靠性.Pan等[20 ] 模拟了电极浆料的狭缝涂布过程,分析了上游模头区域、下游模头区域、自由流动区域中电极浆料流动类型的差异,提出了泊肃叶流-库埃特流-气泡流(Poiseuille-Couette-bubbly flow)的流型转化机制,为寻找稳定涂布窗口提供了理论依据.Malakhov等[21 ] 将涂布速度、黏度、表面张力、模头高度以及涂层膜厚进行了无量纲化,构建了低流量限制模型,预测了在特定浆料性质和模头形状下能够实现的最小无缺陷膜厚,与实验结果对比验证了其有效性.在上述研究中,没有对模头主要尺寸与稳定涂布窗口之间的关联进行系统性分析,研究结果难以直接为工业生产中涂布工艺参数优化提供借鉴. ...
1
... 狭缝涂布过程主要分为两个阶段,电极浆料首先经由外部管道和模头内部流道输送至出口处,然后与集流体发生接触,流经模唇并在模头外部的开放空间中自由流动形成电极涂层.对于模头内部流道的研究通常以提高浆料流动的均匀性为目标,目前已有较多研究[11 -12 ] .电极浆料与集流体接触后,首先在滚动的集流体和固定的模头之间形成剪切流,随后离开模头自由流动,这一过程直接决定了电极涂层的结构.因此,本文假设浆料在到达模头出口附近时稳定流动,研究后续的电极涂层形成过程.Akbarzadeh等[13 ] 研究了电极颗粒、浆料溶剂以及模头边界之间的相互作用,结果表明在涂布过程中电极颗粒的移动路线与浆料的流线高度重叠,并且在低流速区域内相互吸引产生团聚,导致电极颗粒分布得不均匀.因此,流体的流动情况可以体现电极颗粒的行为,保证强度适中的流动是形成稳定涂层的关键.相对于显式粒子模型,将颗粒与溶剂视为整体流体的连续介质模型能够在体现流体主要行为的同时大幅降低计算成本[14 -17 ] .Ahn等[18 ] 和Bhamidipati等[19 ] 分别采用牛顿流体和剪切稀化的非牛顿流体进行了狭缝涂布的实验,并采用相场-流场耦合的模型进行了数值模拟,模拟结果与实验高度一致,表明此类模型具有良好的可靠性.Pan等[20 ] 模拟了电极浆料的狭缝涂布过程,分析了上游模头区域、下游模头区域、自由流动区域中电极浆料流动类型的差异,提出了泊肃叶流-库埃特流-气泡流(Poiseuille-Couette-bubbly flow)的流型转化机制,为寻找稳定涂布窗口提供了理论依据.Malakhov等[21 ] 将涂布速度、黏度、表面张力、模头高度以及涂层膜厚进行了无量纲化,构建了低流量限制模型,预测了在特定浆料性质和模头形状下能够实现的最小无缺陷膜厚,与实验结果对比验证了其有效性.在上述研究中,没有对模头主要尺寸与稳定涂布窗口之间的关联进行系统性分析,研究结果难以直接为工业生产中涂布工艺参数优化提供借鉴. ...
1
... 狭缝涂布过程主要分为两个阶段,电极浆料首先经由外部管道和模头内部流道输送至出口处,然后与集流体发生接触,流经模唇并在模头外部的开放空间中自由流动形成电极涂层.对于模头内部流道的研究通常以提高浆料流动的均匀性为目标,目前已有较多研究[11 -12 ] .电极浆料与集流体接触后,首先在滚动的集流体和固定的模头之间形成剪切流,随后离开模头自由流动,这一过程直接决定了电极涂层的结构.因此,本文假设浆料在到达模头出口附近时稳定流动,研究后续的电极涂层形成过程.Akbarzadeh等[13 ] 研究了电极颗粒、浆料溶剂以及模头边界之间的相互作用,结果表明在涂布过程中电极颗粒的移动路线与浆料的流线高度重叠,并且在低流速区域内相互吸引产生团聚,导致电极颗粒分布得不均匀.因此,流体的流动情况可以体现电极颗粒的行为,保证强度适中的流动是形成稳定涂层的关键.相对于显式粒子模型,将颗粒与溶剂视为整体流体的连续介质模型能够在体现流体主要行为的同时大幅降低计算成本[14 -17 ] .Ahn等[18 ] 和Bhamidipati等[19 ] 分别采用牛顿流体和剪切稀化的非牛顿流体进行了狭缝涂布的实验,并采用相场-流场耦合的模型进行了数值模拟,模拟结果与实验高度一致,表明此类模型具有良好的可靠性.Pan等[20 ] 模拟了电极浆料的狭缝涂布过程,分析了上游模头区域、下游模头区域、自由流动区域中电极浆料流动类型的差异,提出了泊肃叶流-库埃特流-气泡流(Poiseuille-Couette-bubbly flow)的流型转化机制,为寻找稳定涂布窗口提供了理论依据.Malakhov等[21 ] 将涂布速度、黏度、表面张力、模头高度以及涂层膜厚进行了无量纲化,构建了低流量限制模型,预测了在特定浆料性质和模头形状下能够实现的最小无缺陷膜厚,与实验结果对比验证了其有效性.在上述研究中,没有对模头主要尺寸与稳定涂布窗口之间的关联进行系统性分析,研究结果难以直接为工业生产中涂布工艺参数优化提供借鉴. ...
1
... 狭缝涂布过程主要分为两个阶段,电极浆料首先经由外部管道和模头内部流道输送至出口处,然后与集流体发生接触,流经模唇并在模头外部的开放空间中自由流动形成电极涂层.对于模头内部流道的研究通常以提高浆料流动的均匀性为目标,目前已有较多研究[11 -12 ] .电极浆料与集流体接触后,首先在滚动的集流体和固定的模头之间形成剪切流,随后离开模头自由流动,这一过程直接决定了电极涂层的结构.因此,本文假设浆料在到达模头出口附近时稳定流动,研究后续的电极涂层形成过程.Akbarzadeh等[13 ] 研究了电极颗粒、浆料溶剂以及模头边界之间的相互作用,结果表明在涂布过程中电极颗粒的移动路线与浆料的流线高度重叠,并且在低流速区域内相互吸引产生团聚,导致电极颗粒分布得不均匀.因此,流体的流动情况可以体现电极颗粒的行为,保证强度适中的流动是形成稳定涂层的关键.相对于显式粒子模型,将颗粒与溶剂视为整体流体的连续介质模型能够在体现流体主要行为的同时大幅降低计算成本[14 -17 ] .Ahn等[18 ] 和Bhamidipati等[19 ] 分别采用牛顿流体和剪切稀化的非牛顿流体进行了狭缝涂布的实验,并采用相场-流场耦合的模型进行了数值模拟,模拟结果与实验高度一致,表明此类模型具有良好的可靠性.Pan等[20 ] 模拟了电极浆料的狭缝涂布过程,分析了上游模头区域、下游模头区域、自由流动区域中电极浆料流动类型的差异,提出了泊肃叶流-库埃特流-气泡流(Poiseuille-Couette-bubbly flow)的流型转化机制,为寻找稳定涂布窗口提供了理论依据.Malakhov等[21 ] 将涂布速度、黏度、表面张力、模头高度以及涂层膜厚进行了无量纲化,构建了低流量限制模型,预测了在特定浆料性质和模头形状下能够实现的最小无缺陷膜厚,与实验结果对比验证了其有效性.在上述研究中,没有对模头主要尺寸与稳定涂布窗口之间的关联进行系统性分析,研究结果难以直接为工业生产中涂布工艺参数优化提供借鉴. ...
1
... 电极浆料为具有剪切稀化黏度的非牛顿流体,本工作采用Huang等[16 ] 实验测定的物性参数.浆料密度 ρ l 为1320 kg/m3 ,表面张力 σ
1
... 狭缝涂布过程主要分为两个阶段,电极浆料首先经由外部管道和模头内部流道输送至出口处,然后与集流体发生接触,流经模唇并在模头外部的开放空间中自由流动形成电极涂层.对于模头内部流道的研究通常以提高浆料流动的均匀性为目标,目前已有较多研究[11 -12 ] .电极浆料与集流体接触后,首先在滚动的集流体和固定的模头之间形成剪切流,随后离开模头自由流动,这一过程直接决定了电极涂层的结构.因此,本文假设浆料在到达模头出口附近时稳定流动,研究后续的电极涂层形成过程.Akbarzadeh等[13 ] 研究了电极颗粒、浆料溶剂以及模头边界之间的相互作用,结果表明在涂布过程中电极颗粒的移动路线与浆料的流线高度重叠,并且在低流速区域内相互吸引产生团聚,导致电极颗粒分布得不均匀.因此,流体的流动情况可以体现电极颗粒的行为,保证强度适中的流动是形成稳定涂层的关键.相对于显式粒子模型,将颗粒与溶剂视为整体流体的连续介质模型能够在体现流体主要行为的同时大幅降低计算成本[14 -17 ] .Ahn等[18 ] 和Bhamidipati等[19 ] 分别采用牛顿流体和剪切稀化的非牛顿流体进行了狭缝涂布的实验,并采用相场-流场耦合的模型进行了数值模拟,模拟结果与实验高度一致,表明此类模型具有良好的可靠性.Pan等[20 ] 模拟了电极浆料的狭缝涂布过程,分析了上游模头区域、下游模头区域、自由流动区域中电极浆料流动类型的差异,提出了泊肃叶流-库埃特流-气泡流(Poiseuille-Couette-bubbly flow)的流型转化机制,为寻找稳定涂布窗口提供了理论依据.Malakhov等[21 ] 将涂布速度、黏度、表面张力、模头高度以及涂层膜厚进行了无量纲化,构建了低流量限制模型,预测了在特定浆料性质和模头形状下能够实现的最小无缺陷膜厚,与实验结果对比验证了其有效性.在上述研究中,没有对模头主要尺寸与稳定涂布窗口之间的关联进行系统性分析,研究结果难以直接为工业生产中涂布工艺参数优化提供借鉴. ...
2
... 狭缝涂布过程主要分为两个阶段,电极浆料首先经由外部管道和模头内部流道输送至出口处,然后与集流体发生接触,流经模唇并在模头外部的开放空间中自由流动形成电极涂层.对于模头内部流道的研究通常以提高浆料流动的均匀性为目标,目前已有较多研究[11 -12 ] .电极浆料与集流体接触后,首先在滚动的集流体和固定的模头之间形成剪切流,随后离开模头自由流动,这一过程直接决定了电极涂层的结构.因此,本文假设浆料在到达模头出口附近时稳定流动,研究后续的电极涂层形成过程.Akbarzadeh等[13 ] 研究了电极颗粒、浆料溶剂以及模头边界之间的相互作用,结果表明在涂布过程中电极颗粒的移动路线与浆料的流线高度重叠,并且在低流速区域内相互吸引产生团聚,导致电极颗粒分布得不均匀.因此,流体的流动情况可以体现电极颗粒的行为,保证强度适中的流动是形成稳定涂层的关键.相对于显式粒子模型,将颗粒与溶剂视为整体流体的连续介质模型能够在体现流体主要行为的同时大幅降低计算成本[14 -17 ] .Ahn等[18 ] 和Bhamidipati等[19 ] 分别采用牛顿流体和剪切稀化的非牛顿流体进行了狭缝涂布的实验,并采用相场-流场耦合的模型进行了数值模拟,模拟结果与实验高度一致,表明此类模型具有良好的可靠性.Pan等[20 ] 模拟了电极浆料的狭缝涂布过程,分析了上游模头区域、下游模头区域、自由流动区域中电极浆料流动类型的差异,提出了泊肃叶流-库埃特流-气泡流(Poiseuille-Couette-bubbly flow)的流型转化机制,为寻找稳定涂布窗口提供了理论依据.Malakhov等[21 ] 将涂布速度、黏度、表面张力、模头高度以及涂层膜厚进行了无量纲化,构建了低流量限制模型,预测了在特定浆料性质和模头形状下能够实现的最小无缺陷膜厚,与实验结果对比验证了其有效性.在上述研究中,没有对模头主要尺寸与稳定涂布窗口之间的关联进行系统性分析,研究结果难以直接为工业生产中涂布工艺参数优化提供借鉴. ...
... 根据文献[8 -9 ]中的实验工况,采用二维模型进行有限元模拟.模拟中所采用的控制方程、边界条件以及空气的物性参数均与上文中一致,模型的几何尺寸及浆料的物性参数的设置与文献一致:在与Ahn等[18 ] 的实验结果进行对比时,狭缝宽度、模头高度、表面张力均与本工作所采用的一致,浆料为μ l =0.045 Pa∙ s的牛顿流体,浆料与模头、集流体之间的接触角均为60°;在与Bhamidipati等[19 ] 的实验结果进行对比时,狭缝宽度为0.25 mm,模头高度为0.25 mm,浆料的流体一致性系数为8.07 Pa∙ s,流动特性指数为0.83,表面张力为0.047 N/m,浆料与模头、集流体之间的接触角分别为69°和62°.稳定涂布窗口即为每个涂布速度所对应的使涂布稳定进行的进料速度的范围,具体的判定标准在下文详细叙述.通过模拟结果与文献中实验结果确定的稳定涂布窗口如图3 所示,本文中的模型展现出较高的准确性和通用性. ...
2
... 狭缝涂布过程主要分为两个阶段,电极浆料首先经由外部管道和模头内部流道输送至出口处,然后与集流体发生接触,流经模唇并在模头外部的开放空间中自由流动形成电极涂层.对于模头内部流道的研究通常以提高浆料流动的均匀性为目标,目前已有较多研究[11 -12 ] .电极浆料与集流体接触后,首先在滚动的集流体和固定的模头之间形成剪切流,随后离开模头自由流动,这一过程直接决定了电极涂层的结构.因此,本文假设浆料在到达模头出口附近时稳定流动,研究后续的电极涂层形成过程.Akbarzadeh等[13 ] 研究了电极颗粒、浆料溶剂以及模头边界之间的相互作用,结果表明在涂布过程中电极颗粒的移动路线与浆料的流线高度重叠,并且在低流速区域内相互吸引产生团聚,导致电极颗粒分布得不均匀.因此,流体的流动情况可以体现电极颗粒的行为,保证强度适中的流动是形成稳定涂层的关键.相对于显式粒子模型,将颗粒与溶剂视为整体流体的连续介质模型能够在体现流体主要行为的同时大幅降低计算成本[14 -17 ] .Ahn等[18 ] 和Bhamidipati等[19 ] 分别采用牛顿流体和剪切稀化的非牛顿流体进行了狭缝涂布的实验,并采用相场-流场耦合的模型进行了数值模拟,模拟结果与实验高度一致,表明此类模型具有良好的可靠性.Pan等[20 ] 模拟了电极浆料的狭缝涂布过程,分析了上游模头区域、下游模头区域、自由流动区域中电极浆料流动类型的差异,提出了泊肃叶流-库埃特流-气泡流(Poiseuille-Couette-bubbly flow)的流型转化机制,为寻找稳定涂布窗口提供了理论依据.Malakhov等[21 ] 将涂布速度、黏度、表面张力、模头高度以及涂层膜厚进行了无量纲化,构建了低流量限制模型,预测了在特定浆料性质和模头形状下能够实现的最小无缺陷膜厚,与实验结果对比验证了其有效性.在上述研究中,没有对模头主要尺寸与稳定涂布窗口之间的关联进行系统性分析,研究结果难以直接为工业生产中涂布工艺参数优化提供借鉴. ...
... 根据文献[8 -9 ]中的实验工况,采用二维模型进行有限元模拟.模拟中所采用的控制方程、边界条件以及空气的物性参数均与上文中一致,模型的几何尺寸及浆料的物性参数的设置与文献一致:在与Ahn等[18 ] 的实验结果进行对比时,狭缝宽度、模头高度、表面张力均与本工作所采用的一致,浆料为μ l =0.045 Pa∙ s的牛顿流体,浆料与模头、集流体之间的接触角均为60°;在与Bhamidipati等[19 ] 的实验结果进行对比时,狭缝宽度为0.25 mm,模头高度为0.25 mm,浆料的流体一致性系数为8.07 Pa∙ s,流动特性指数为0.83,表面张力为0.047 N/m,浆料与模头、集流体之间的接触角分别为69°和62°.稳定涂布窗口即为每个涂布速度所对应的使涂布稳定进行的进料速度的范围,具体的判定标准在下文详细叙述.通过模拟结果与文献中实验结果确定的稳定涂布窗口如图3 所示,本文中的模型展现出较高的准确性和通用性. ...
1
... 狭缝涂布过程主要分为两个阶段,电极浆料首先经由外部管道和模头内部流道输送至出口处,然后与集流体发生接触,流经模唇并在模头外部的开放空间中自由流动形成电极涂层.对于模头内部流道的研究通常以提高浆料流动的均匀性为目标,目前已有较多研究[11 -12 ] .电极浆料与集流体接触后,首先在滚动的集流体和固定的模头之间形成剪切流,随后离开模头自由流动,这一过程直接决定了电极涂层的结构.因此,本文假设浆料在到达模头出口附近时稳定流动,研究后续的电极涂层形成过程.Akbarzadeh等[13 ] 研究了电极颗粒、浆料溶剂以及模头边界之间的相互作用,结果表明在涂布过程中电极颗粒的移动路线与浆料的流线高度重叠,并且在低流速区域内相互吸引产生团聚,导致电极颗粒分布得不均匀.因此,流体的流动情况可以体现电极颗粒的行为,保证强度适中的流动是形成稳定涂层的关键.相对于显式粒子模型,将颗粒与溶剂视为整体流体的连续介质模型能够在体现流体主要行为的同时大幅降低计算成本[14 -17 ] .Ahn等[18 ] 和Bhamidipati等[19 ] 分别采用牛顿流体和剪切稀化的非牛顿流体进行了狭缝涂布的实验,并采用相场-流场耦合的模型进行了数值模拟,模拟结果与实验高度一致,表明此类模型具有良好的可靠性.Pan等[20 ] 模拟了电极浆料的狭缝涂布过程,分析了上游模头区域、下游模头区域、自由流动区域中电极浆料流动类型的差异,提出了泊肃叶流-库埃特流-气泡流(Poiseuille-Couette-bubbly flow)的流型转化机制,为寻找稳定涂布窗口提供了理论依据.Malakhov等[21 ] 将涂布速度、黏度、表面张力、模头高度以及涂层膜厚进行了无量纲化,构建了低流量限制模型,预测了在特定浆料性质和模头形状下能够实现的最小无缺陷膜厚,与实验结果对比验证了其有效性.在上述研究中,没有对模头主要尺寸与稳定涂布窗口之间的关联进行系统性分析,研究结果难以直接为工业生产中涂布工艺参数优化提供借鉴. ...
1
... 狭缝涂布过程主要分为两个阶段,电极浆料首先经由外部管道和模头内部流道输送至出口处,然后与集流体发生接触,流经模唇并在模头外部的开放空间中自由流动形成电极涂层.对于模头内部流道的研究通常以提高浆料流动的均匀性为目标,目前已有较多研究[11 -12 ] .电极浆料与集流体接触后,首先在滚动的集流体和固定的模头之间形成剪切流,随后离开模头自由流动,这一过程直接决定了电极涂层的结构.因此,本文假设浆料在到达模头出口附近时稳定流动,研究后续的电极涂层形成过程.Akbarzadeh等[13 ] 研究了电极颗粒、浆料溶剂以及模头边界之间的相互作用,结果表明在涂布过程中电极颗粒的移动路线与浆料的流线高度重叠,并且在低流速区域内相互吸引产生团聚,导致电极颗粒分布得不均匀.因此,流体的流动情况可以体现电极颗粒的行为,保证强度适中的流动是形成稳定涂层的关键.相对于显式粒子模型,将颗粒与溶剂视为整体流体的连续介质模型能够在体现流体主要行为的同时大幅降低计算成本[14 -17 ] .Ahn等[18 ] 和Bhamidipati等[19 ] 分别采用牛顿流体和剪切稀化的非牛顿流体进行了狭缝涂布的实验,并采用相场-流场耦合的模型进行了数值模拟,模拟结果与实验高度一致,表明此类模型具有良好的可靠性.Pan等[20 ] 模拟了电极浆料的狭缝涂布过程,分析了上游模头区域、下游模头区域、自由流动区域中电极浆料流动类型的差异,提出了泊肃叶流-库埃特流-气泡流(Poiseuille-Couette-bubbly flow)的流型转化机制,为寻找稳定涂布窗口提供了理论依据.Malakhov等[21 ] 将涂布速度、黏度、表面张力、模头高度以及涂层膜厚进行了无量纲化,构建了低流量限制模型,预测了在特定浆料性质和模头形状下能够实现的最小无缺陷膜厚,与实验结果对比验证了其有效性.在上述研究中,没有对模头主要尺寸与稳定涂布窗口之间的关联进行系统性分析,研究结果难以直接为工业生产中涂布工艺参数优化提供借鉴. ...