目前,正处于开发中的大规模储电系统主要包括抽水蓄能系统(PHS)、压缩空气储能系统(CAES)、液流电池系统(FB)以及本工作讨论的热泵储电系统(PTES),又称为卡诺电池(CB)等。卡诺电池技术是一种新型的大规模物理储能技术,该技术以热能的形式将能量存储下来并在需要时以机械能的形式向外输出,其不受地理位置限制且可针对传统煤电站进行改造[3]。一般根据采用的热力循环种类的不同,卡诺电池可分为以下3类:基于跨临界二氧化碳循环、朗肯循环以及布雷顿循环的卡诺电池。
2010年,Desrues等[4]提出了1种基于布雷顿循环的卡诺电池系统并建立了容量为602.6 MWh的一维瞬态模型。结果表明,当充电时间约6 h后,该卡诺电池可以放电约5 h,且系统往返效率高达66.7%。Howes[5]采用往复式压缩膨胀机替代了旋转式热功转换机械并研究了理想条件下以氩气作为工质的系统热力学性能。在氩气的质量流量为12.56 kg/s,蓄热罐温度/运行压力为500 ℃/1.213 MPa,蓄冷罐温度/运行压力为-166 ℃/常压的工况下,额定功率为2 MW,储能量为16 MWh的卡诺电池的往返效率可达0.72。Xue等[6]建立了基于相变堆积床的卡诺电池一维瞬态模型并比较了显热和潜热储存的能量密度差异。结果表明,两者的体积储能密度分别为202.4、267.4 kWh/m3,相较于显热存储,相变堆积床的储能密度提升了32.1%。
1 卡诺电池系统原理与建模
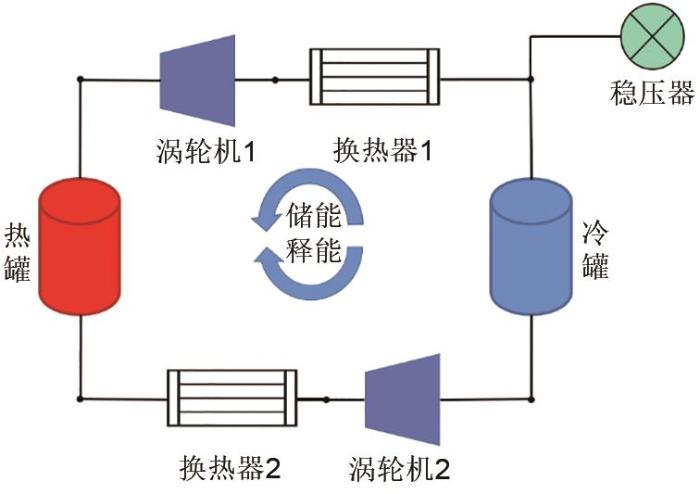
如图1所示,卡诺电池分为以下几个主要部分:储热/储冷罐,两台涡轮机,两个换热器,稳压器及与之配套的阀门、循环风扇等设备。其中,两台涡轮机械在系统运行的储能/释能过程中,根据工质流动方向不同,分别作为压缩-膨胀机对使用。两个储罐内部则分别放置储热、储冷所需的储能介质,通过与流经的工质发生热交换实现能量的储存与释放。两台换热器用以补偿系统的不可逆带来的余热,以稳定两台涡轮机械入口处工质的温度,使系统的运行更加平稳,同时吸收一部分余热、余冷加以利用。稳压器用于维持气体工质的流量与压力以消除流动损失等因素对系统的影响。
图1
在储能过程中,气体沿逆时针方向流动,常温常压的工质在涡轮机1中被压缩,消耗外界输入的电能,将工质压缩至高温高压状态。随后气体流经热罐,与罐内的储热介质发生热交换并释放热量,储热介质的温度逐渐升高。中温高压的气体流出热罐后进入换热器2,向外界继续释放热量。此时仍保持高压的气体工质进入涡轮机2中膨胀至低温低压,这一阶段涡轮机2作为膨胀机向外输出机械能,带动发电机产生电能。与热罐类似,低温低压的气体进入冷罐与储冷介质发生热交换,储冷介质的温度逐渐降低。经由冷罐流出的工质在换热器1中继续吸热,达到初始的常温常压状态,完成储能过程。当两个储罐内储存的热量/冷量达到设计值时,认为储能过程完成。在释能过程中,工质的流向相反,沿顺时针流动,具体过程与储能过程类似。此外,值得注意的是,冷罐、热罐分别设置了直接向外界供冷、供热的回路,可在释能循环外单独输出冷量、热量。
为了降低系统的复杂性,重点关注换热过程中占主导地位的过程及参数,做出如下简化假设:
(1)储能罐的外层壁面绝热,忽略储能罐顶部和底部的热损失;
(2)压缩机和膨胀机的等熵效率为常数,不随工质的状态参数变化而改变;
(3)忽略包覆材料壁面热阻,忽略管道沿程等压力损失,忽略稳压器能量消耗;
(4)相变介质的热物性只与状态有关,储能罐内仅沿轴向流动和传热。
(5)电能与技术功之间的转换效率为1。
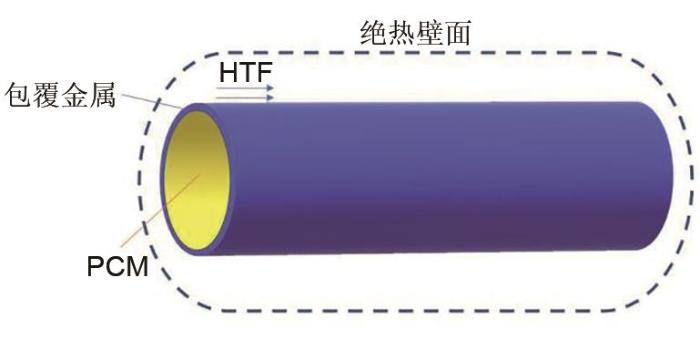
如图2所示,储能罐是一个外部形状为圆柱的压力容器,其壁面由隔热材料制成,并做保温处理以减少热损失。其内侧布置有包覆了相变储热介质的金属圆柱体,起到密封与增强换热的作用。工质从储能罐的一端流入,沿水平方向从另一端流出,期间与储能介质发生热交换,以实现储能罐的储能或释能。采用均匀网格、一维有限体积法对储能罐进行显式差分形式的离散,储能罐沿工质流动方向被均分为n个储热单元体。
图2
相变储热介质储存的能量QPCM根据其液相含量f(0 ≤ f ≤ 1)的不同,可以表示为
式中,T0为环境温度;Tp为相变温度;mPCM为相变储热介质的质量;cp,PCM,s、cp,PCM,l分别为介质在固态、液态时的比热容;L为相变焓。
工质外掠圆柱体金属发生对流换热的表面换热系数hx 表示为
式中,x为特征长度;λ为工质的热导率。
Rex 、Prx 的计算式为
式中,uHTF、ν、ρHTF、cp 分别为工质的流速、黏度、密度、定压比热容。
涡轮机进、出口处工质的温度、压力关系可以表示为
式中,β为压缩(膨胀)比;η为等熵效率;Tin、Tout、pin、pout分别为压缩机的进、出口处的温度、压力;绝热指数к=cp /cV。
涡轮机械消耗(产生)的功率可以表示为
式中,ṁt为工质的质量流量;hHX,out、hHX,in分别为出口、入口处工质的比焓。
工质经过换热器向外释放的热流率可以表示为
式中,ṁHX为工质的质量流量。
根据前文所述的建模过程,卡诺电池系统一维瞬态模型的设计参数与材料热物性见表1。
表1 卡诺电池系统的运行参数与相变介质热物性
Table 1
| 参数/单位 | 储热罐 | 储冷罐 |
|---|---|---|
| 储能介质 | NaOH粉末 | 质量分数15% CaCl2水溶液 |
| 长度l/m | 5 | 5 |
| 直径D/m | 4 | 3 |
| 体积V/m3 | 121 | 81 |
| 压缩比β | 10 | |
| 等熵效率η | 0.9 | |
| 相变温度Tp/K | 491 | 228 |
| 相变潜热L/(kJ/kg) | 284 | 160 |
| 密度ρ/(kg/m3) | 2130 | 1286 |
| 固态比热容cp,s/[kJ/(kg·K)] | 2.9 | 2.6 |
| 液态比热容cp,l /[kJ/(kg·K)] | 2.1 | 2 |
| 热导率λ/[W/(m·K)] | 0.6 | 1.1 |
卡诺电池的系统性能指标主要包括功率密度、储能密度和系统往返效率。其中,功率密度ρP 表示为
式中,Pt,dis为系统在释能过程中向外输出的技术功功率;VHR、VCR分别为储热罐、储冷罐的体积。
储能密度ρE表示为
式中,QHR
往返效率RTE表示为
式中,Wt,dis、Wt,chr分别为系统释能过程向外输出、储能过程消耗的技术功。
为研究系统运行过程中的一般规律,选用恰当的特征量尺度将控制方程无量纲化。在本工作中,主要对温度、时间和距离做无量纲化处理,无量纲温度θ、时间τ*、距离x*可以表示为[6]
根据式(1)~
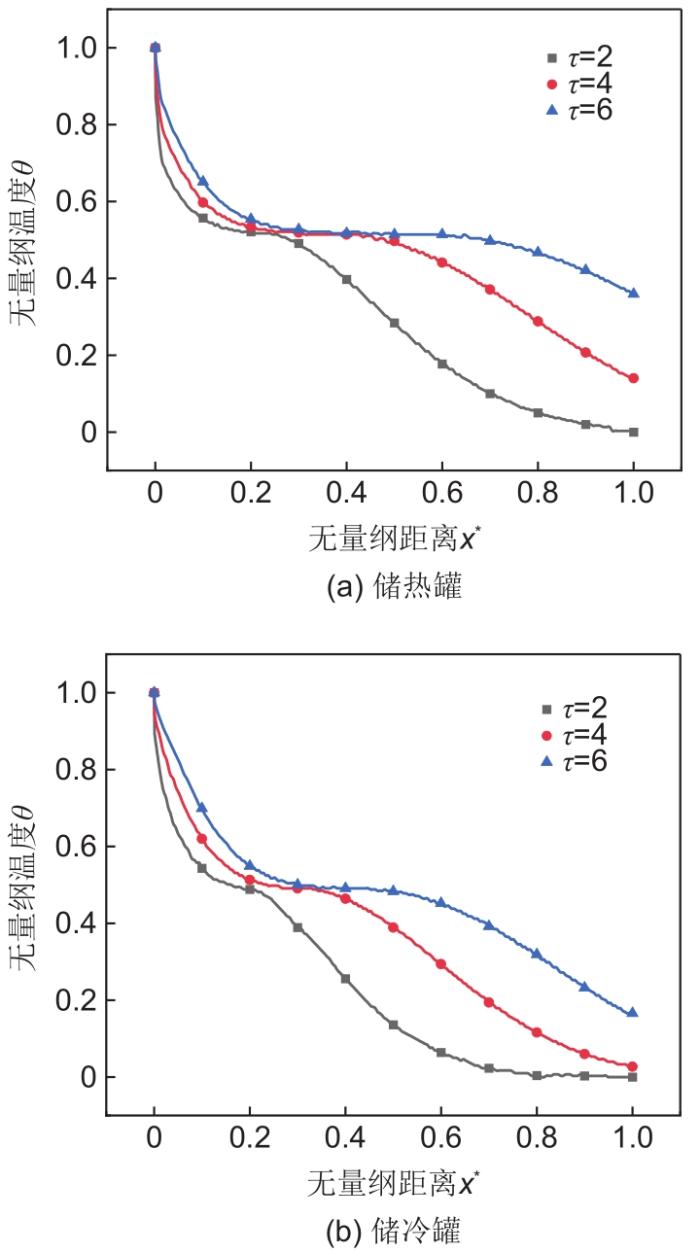
图3展示了在储能过程中储热罐与储冷罐在不同时刻时,罐内相变储能介质温度随轴向距离的分布情况。以储热罐为例,根据储能介质的不同状态,可以将罐内沿轴向依次划分为3段:液相段、两相段、固相段。图中可以看出存在一个无量纲温度的平台期,这对应了两相共存的阶段,在这个过程中储能介质的温度几乎不变,从气体工质中吸收的能量全部转化为相变过程所需的潜热,直至相变过程结束。热罐在靠近入口处属于液相段,随着距离的增加,介质温度逐渐从入口处工质温度降低至相变温度,且温度对距离的变化率逐渐减缓。这是由于随着工质的流动,其传热温差逐渐降低,传热的速率逐渐减缓,从而使得温度梯度逐渐降低。随着时间的推移,介质的温度不断增加,温差较大的斜温层不断向出口处移动,介质中储存的热量逐渐增加。类似的,储冷罐同样可以分为3段,但是靠近入口处为液相段,靠近出口处为固相段,且无量纲温度越高,实际上相变介质的温度越低。因此,随着时间的推移,储冷罐中介质的温度不断降低,温差较大的斜温层不断向出口处移动,介质中储存的冷量逐渐增加,这也使得靠近出口处的相变介质逐渐开始固化,体现为固相段的长度逐渐增加,两相段逐渐向后移动。对比冷热罐,可以发现热罐中随着储能过程的进行,其两相平台段的长度逐渐增加,这是因为由于工质和介质间的温差逐渐减小,传热的速率逐渐降低,因此完成吸热液化过程所需的时间更长,表现两相段的长度更长。冷罐中这一趋势体现得并不明显,主要是由于相变介质的物性决定的,储冷介质相变潜热与比热容的比值相比储热介质较小,故完成相变过程所需的冷量在整个储冷过程中的占比较小,表现为两相段的长度整体小于储热过程,随时间的增长而增长的过程更不明显。
图3
图3
储能过程相变储热介质的温度分布
Fig. 3
Temperature distribution of phase change heat storage medium in energy storage process
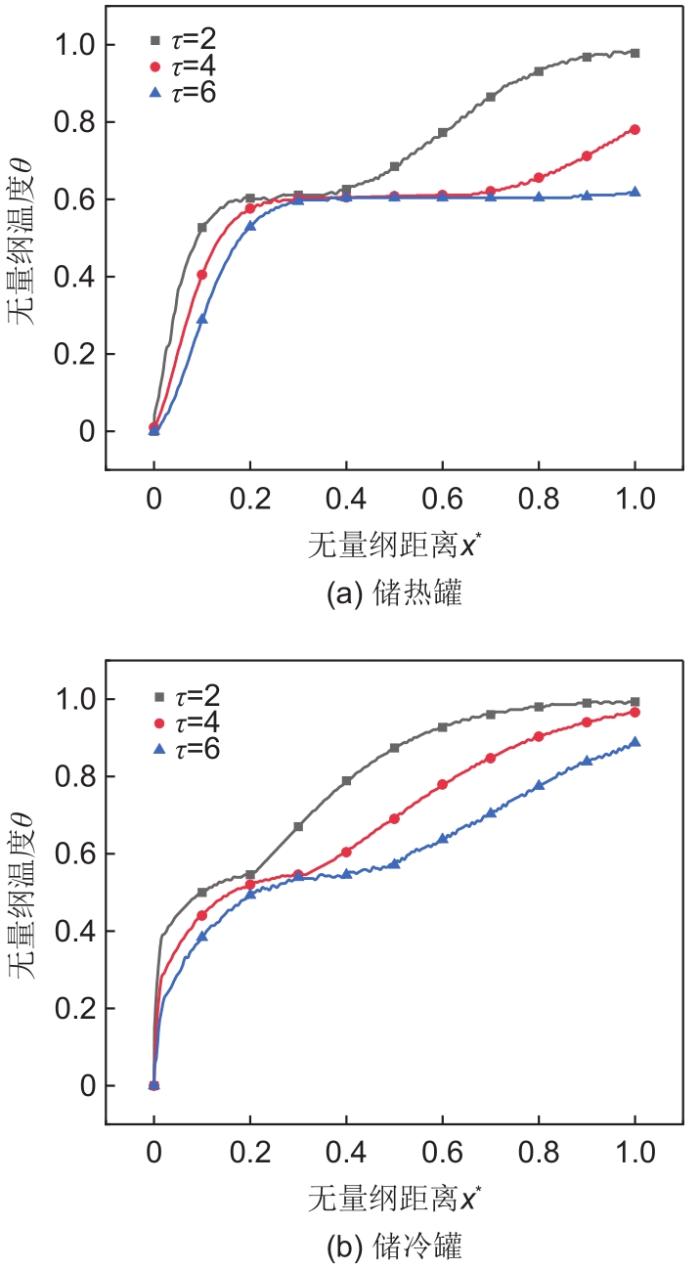
图4揭示了在释能过程不同时刻罐内储能介质温度随轴向距离的分布情况。在储热罐中,沿工质流动方向依次是固相段、两相段、液相段,随着释能过程不断进行,罐内介质的温度逐渐降低,固相段的长度逐渐增加,两相段逐渐向出口处移动,罐内储存的能量也逐渐降低。类似的,在冷罐中,随着释能过程的深入,罐内介质的温度逐渐升高,液相段的长度逐渐增加,两相段逐渐向出口处移动。
图4
图4
释能过程相变储热介质的温度分布
Fig. 4
Temperature distribution of heat storage tank in energy release process
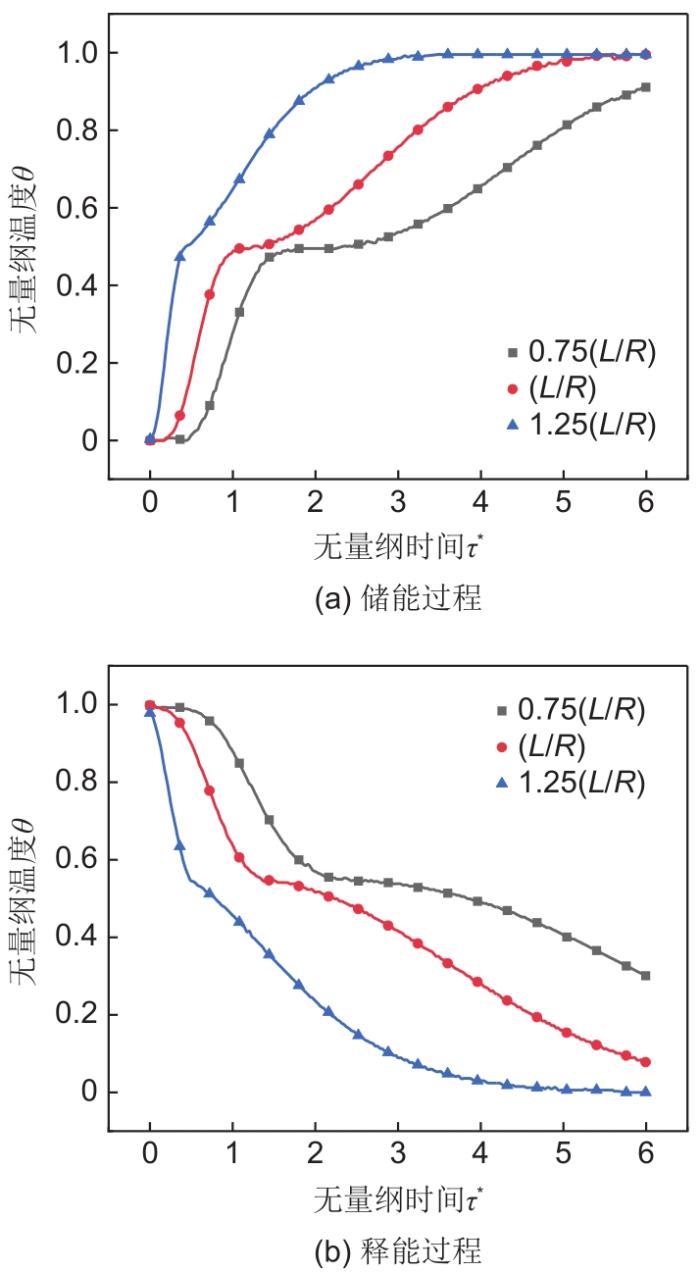
图5展示了在其他条件不变的情况下,改变储能单元的几何结构参数,即长度与半径的比值分别为原来的0.75、1.25倍时,一个循环过程内储热罐内温度随时间的变化情况。在储能过程中,随着长径比从0.75增加至1.25倍,经过相同时间后储热介质的温度更高,储存的热量越多。当无量纲时间为6,长径比为0.75倍时,最终无量纲温度为0.89。当长径比从1倍增加至1.25倍时,达到最大温度的用时从5.44缩短至3.49,即缩短至设计工况的64.2%。这是由于在结构参数变化的过程中,储热单元的结构逐渐变得细长,其横截面积降低,单位长度单元体内的储热介质的温度变化率随之提高。释能过程中能量的变化体现出了类似的规律,长径比从0.75倍增加至1倍时,介质最终无量纲温度从0.31降低至0.08,降低了74.2%;长径比增加至1.5倍时,储热介质已在无量纲时间5.83时降低至最低温度。
图5
图5
长径比对相变储热介质温度变化的影响
Fig. 5
Influence of length-diameter ratio on temperature change of phase change heat storage medium
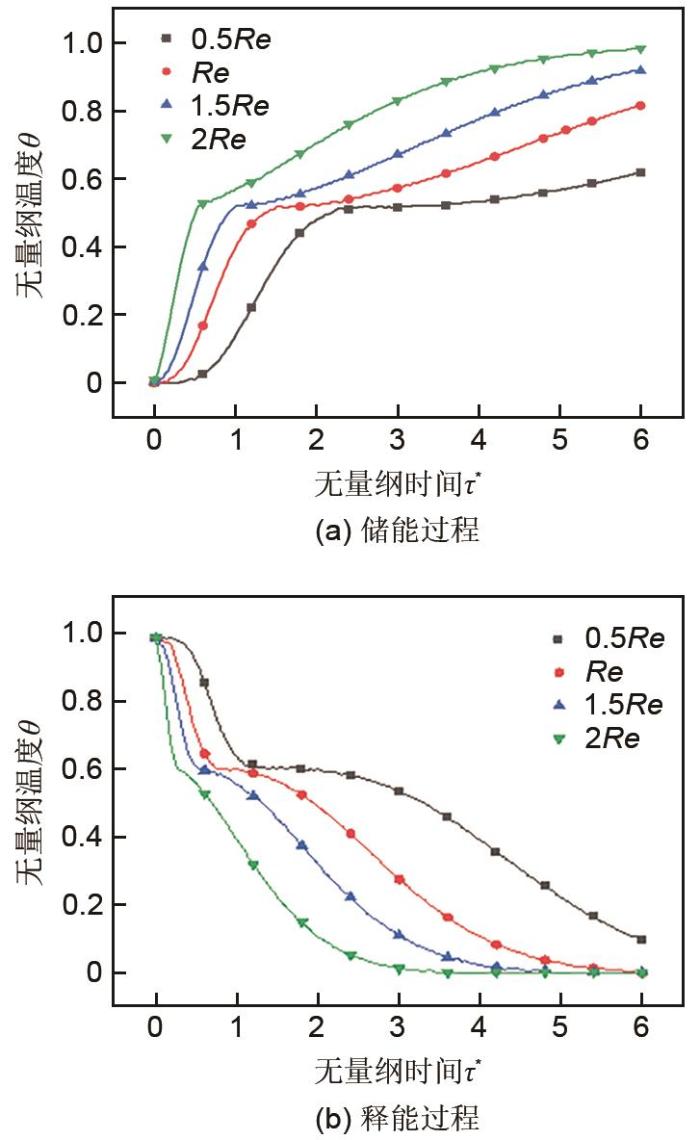
图6展示了在控制其他条件不变时,将储热罐入口处雷诺数分别改变为设计值的0.5、1、1.5、2倍时,储热罐内温度随时间的变化情况。在储能过程中,当雷诺数逐渐从0.5倍增大至2倍时,经过相同时间,储热介质的温度更高且储热介质储存的热量更多。当无量纲时间为6时,根据雷诺数的大小,4种工况的储热介质最终温度分别为0.618、0.814、0.919、0.978,分别对应设计工况最终温度的75.9%、100%、112.9%、117.5%。这是由于雷诺数的增加带来表面对流换热系数的增加,显著改善了换热状况,使得工质与介质间的能量传递功率更大,因此体现为介质的温度提升更快。类似的,释能过程中体现出相同的规律,当雷诺数减小为设计值的一半时,储能介质最终温度为0.139,未达到最小值;当雷诺数分别为设计值的1、1.5、2倍时,储冷介质达到最低温度用时分别为5.63、4.92、3.78,对应设计工况的100%、87.4%、67.1%。
图6
图6
入口处雷诺数对相变储热介质温度的影响
Fig. 6
Effect of Reynolds number at the inlet on temperature of phase change heat storage medium
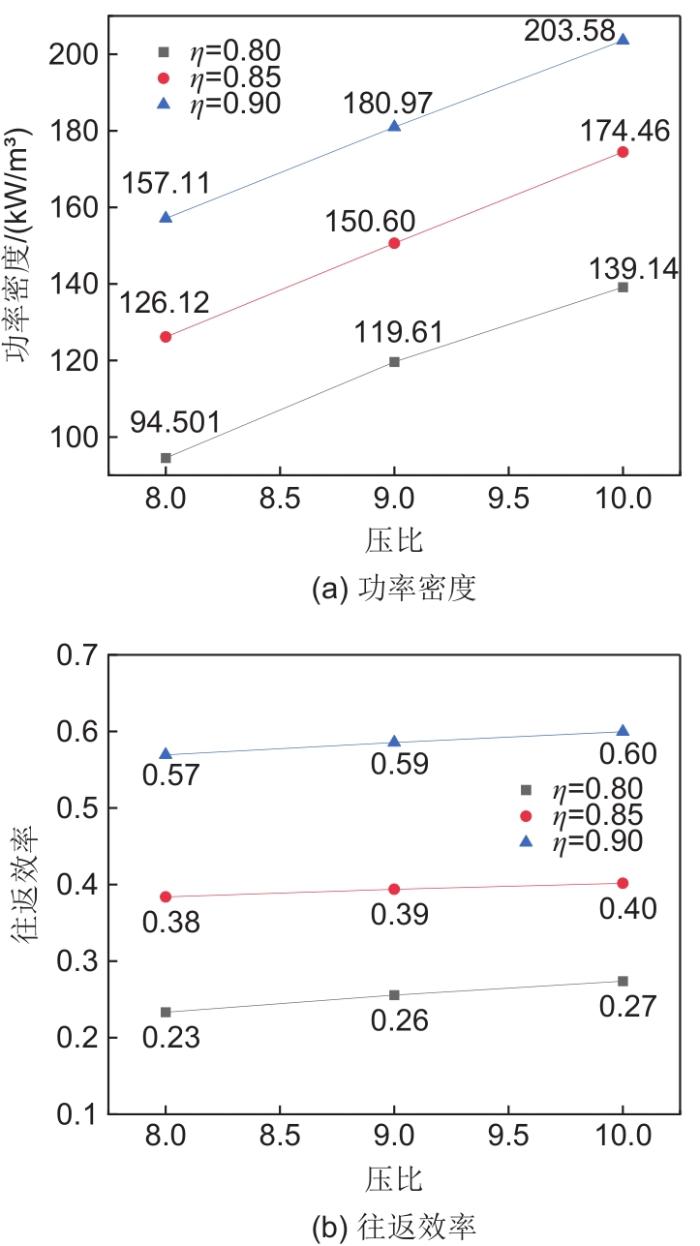
图7
图7
不同工况下系统的功率密度和往返效率值
Fig. 7
Power density and round-trip efficiency values of the system under different working conditions
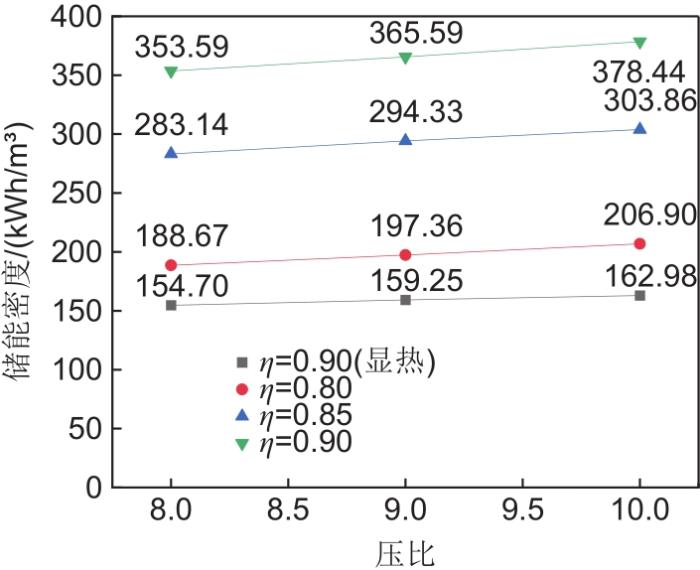
图8展示了在不同的等熵效率以及是否采用相变介质情况下,储能密度与压缩机压比的关系。当等熵效率、压缩比分别增大时,系统的储能密度随之增大,系统容量也随之增大,可以满足更大的电力负荷需求。在设计工况下,采用相变储能介质后,储能密度从162.98增加到378.44 kWh/m3,增幅达到132%,因此引入相变储能技术可以有效减小系统的体积。
图8
图8
不同工况下系统的储能密度值
Fig. 8
Energy storage density values of the system under different working conditions
2 实验研究
图9
图9
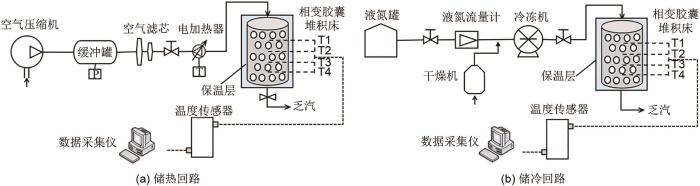
卡诺电池系统实验装置
Fig. 9
Diagram of the experimental setup of the Carnot battery system
图10
图10
实验装置结构
(a) Heat storage circuit; (b) Cold storage circuit
Fig. 10
Structure diagram of experimental setup
表2 实验装置的几何参数
Table 2
| 参数 | 储热罐 | 储冷罐 |
|---|---|---|
| 压力容器高度×外径×厚度/mm | 800×662×12 | 650×512×6 |
| 相邻隔板间距/mm | 250 | 200 |
| 储能介质单元体长度×宽度×高度/mm | 150×150×200 | 100×100×150 |
| 容器个数/个 | 21 | 21 |
| 孔隙率 | 0.62 | 0.71 |
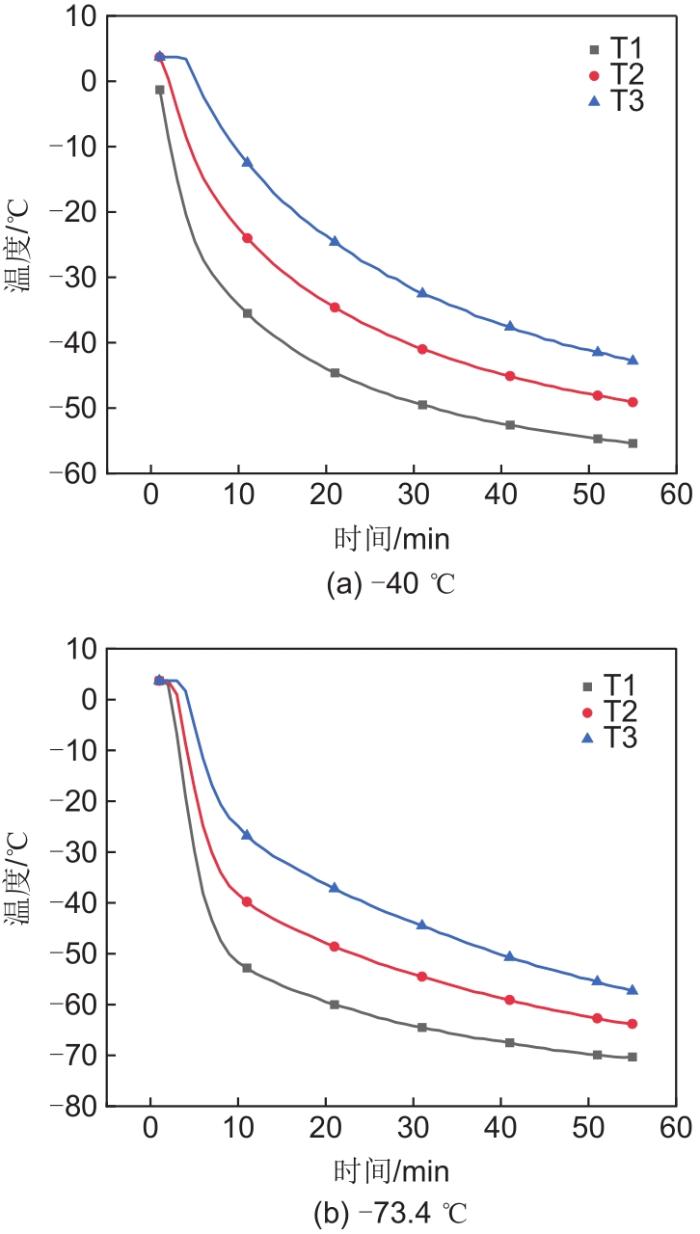
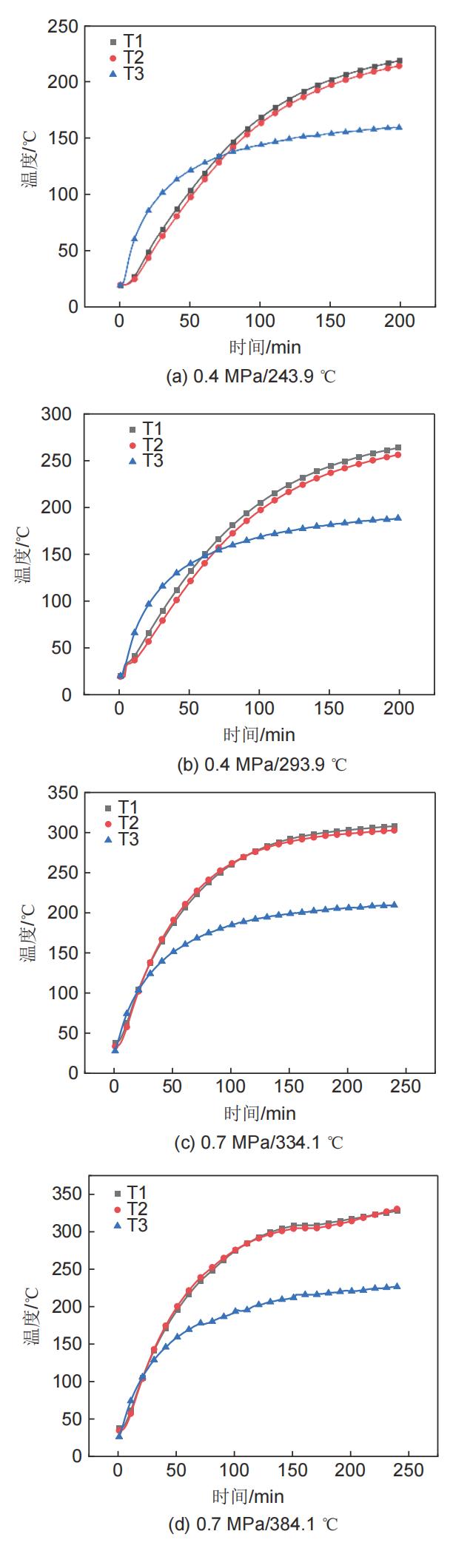
储冷过程开展了两组实验,分别配置了质量分数为15%和25%的氯化钙水溶液,分别查得其相变温度为-14.8和-30.0 ℃。储冷罐中工质的压力为1个标准大气压,通过调节制冷机,设置两次实验的工质的入口温度分别为-40、-73.4 ℃。至于储热过程分别开展了4组实验,由于实验装置中的高温、高压分别由压缩机与电加热器提供,因此设置4种不同的工质入口参数,分别为0.4 MPa/243.9 ℃,0.4 MPa/293.9 ℃,0.6 MPa/307.7 ℃,0.6 MPa/357.7 ℃。参数的选取是考虑到压缩机实际运行过程中的等熵效率不同造成的影响。
储冷罐内相变储冷介质的温度随时间变化情况如图11所示,3条曲线分别为测得罐内不同层储冷单元的温度变化。随着储冷过程的深入,罐内的介质温度不断降低,T1、T2、T3分别测得的最低温度为-55.4、-49.1、-42.8 ℃。沿工质流通的方向,同一时刻不同位置的温度体现出逐渐增加的趋势,最靠近入口处的T1温度最低,最靠近出口处的T3温度最高。初始阶段,温度降低的幅度较大,此时介质和工质间的温差较大,传热速率更高,随着时间的增加,温度的变化逐渐变得平缓,介质与工质温度逐渐接近。(b)方案与(a)方案相比,储存的总冷量更大,增幅为11.3%。图11(b)中由于起始阶段的温差更大,其温度降低的幅度相比(a)更快,最终储冷介质趋近的温度也越低,储能过程中的储冷量越多。
图11
图11
不同工质入口温度下储冷罐内温度分布
Fig. 11
Temperature distribution in the storage tank at different working fluid inlet temperatures
至于储热罐,当运行参数为0.4 MPa时,两组进口温度均低于储热介质发生相变的温度300.8 ℃,此时储热罐内存储的能量全部以显热形式储存。此过程中,随着时间的变化储热介质的温度不断升高,但是变化率逐渐降低。储热罐出口处的工质温度也不断升高,但是升高的幅度逐渐放缓。当入口工质温度增大时,传热的速率也会随之加快,最终达成的趋近温度也更高。这样的趋势是由于随着过程深入,传热温差逐渐降低,传热速率变缓,最终储热介质趋近于工质入口温度。图12(a)、(b)中,两者的储热形式均为显热。在0~200 min内,两者的累计储热量分别为17.5 kWh和21.3 kWh,提升了21.7%;案例2达到案例1的最大储热量18.2 kWh的时间仅为128 min,缩短了108 min。
图12
图12
工质入口参数不同时储热罐内温度分布
Fig. 12
Temperature distribution in the heat storage tank when the working fluid inlet parameters are not the same
另外两组实验的入口参数分别为0.7 MPa/334.1 ℃、0.7 MPa/384.1 ℃,工质入口温度均高于储热介质相变点,当温度到达相变点后开始相变过程。240 min时,两者均发生相变且累计储热量分别达到30.1和35.4 kWh。当温度较低时,储热介质的温度变化较为迅速,这是由于此时温差较大,传热速率较快。随着温度逐渐靠近相变点,温度上升的幅度逐渐放缓。当入口处工质压力不变,但增大温度时,经过相同时刻储热介质的温度更高,传热速率更快。
3 结论
基于相变储热和布雷顿循环的卡诺电池系统由于其高效、紧凑且对地理条件无限制的特点,是一种具有广阔应用前景的大规模长时物理储能技术。本工作设计了一种装机容量10 MWh的卡诺电池系统,并建立了一维瞬态数值模型,讨论了系统内的传热过程与影响因素,并根据选定运行参数进行了实验研究,得到的主要结论如下。
(1)在本系统设计运行参数下,功率密度达到203.6 kW/m3,往返效率达到0.6,储能密度达到378.4 kWh/m3,且随着压缩机压比和等熵效率的增加,系统的功率密度、往返效率、储能密度也会持续增加,但过高的运行参数对材料的和工艺提出了更高的要求。
(2)随着储能单元体长径比和储能罐入口处工质雷诺数的增加,系统的传热过程进度加快,储能/释能功率提高,充放电过程的用时均减少。雷诺数由设计值0.75倍增大至2倍时,工质最终温度由设计值的75.9%增大至117.5%。当长径比从1倍增加至1.25倍时,达到最大温度的无量纲时间从5.44缩短至3.49。长径比从0.75倍增加至1倍时,介质最终无量纲温度从0.31降低至0.08,降低了74.2%。
(3)在实验研究中,验证了工质温度和压力的提升对储热的储能容量和储能功率均有较大的提升。工质压力为0.4 MPa时,当入口温度增加50 ℃,200 min内储热容量分别提升了21.7%;达到最大储热量18.2 kWh的时间缩减了45.7%;当工质压力0.7 MPa,入口温度增加50 ℃时,240 min储热量增加17.6%。
符号说明
| 比热容,kJ/(kg·K) | |
| 能量,kJ | |
| 液相率 | |
| 焓,kJ/kg | |
| 对流换热系数,W/(m2·K) | |
| 相变潜热,kJ/kg | |
| 长度,m | |
| 质量,kg | |
| 普朗特数 | |
| 热量,kJ | |
| 雷诺数 | |
| 往返效率 | |
| 温度,K | |
| 技术功,kJ | |
| 距离,m | |
| 压缩比 | |
| 等熵效率 | |
| 无量纲温度 | |
| 绝热系数 | |
| 热导率,W/(m·K) | |
| 密度,kg/m3 | |
| 时间,s | |
| 储冷罐 | |
| 充电过程 | |
| 放电过程 | |
| 工质流体 | |
| 储热罐 | |
| 换热器 | |
| 入口 | |
| 液态 | |
| 出口 | |
| 固态 |
参考文献