[1]
习近平. 继往开来,开启全球应对气候变化新征程——在气候雄心峰会上的讲话[J]. 中华人民共和国国务院公报, 2020(35): 7.
[本文引用: 1]
[2]
新华社. 习近平主持召开中央财经委员会第九次会议[J]. 预算管理与会计, 2021(4): 4-5.
[本文引用: 1]
[3]
张超. 新能源发电并网对电网电能质量的分析研究[J]. 中国设备工程, 2019(19): 230-231.
[本文引用: 1]
[4]
李建林, 袁晓冬, 郁正纲, 等. 利用储能系统提升电网电能质量研究综述[J]. 电力系统自动化, 2019, 43(8): 15-24.
[本文引用: 1]
LI J L, YUAN X D, YU Z G, et al. Comments on power quality enhancement research for power grid by energy storage system[J]. Automation of Electric Power Systems, 2019, 43(8): 15-24.
[本文引用: 1]
[5]
袁世斐, 吴红杰, 殷承良. 锂离子电池简化电化学模型: 浓度分布估计[J]. 浙江大学学报(工学版), 2017, 51(3): 478-486.
[本文引用: 1]
YUAN S F, WU H J, YIN C L. Simplified electrochemical model for Li-ion battery: Lithium concentration estimation[J]. Journal of Zhejiang University (Engineering Science), 2017, 51(3): 478-486.
[本文引用: 1]
[6]
李云. 锂电池的建模与仿真[D]. 北京: 北方工业大学, 2018.
[本文引用: 1]
LI Y. The modeling and simulation of the lithium-ion battery[D]. Beijing: North China University of Technology, 2018.
[本文引用: 1]
[7]
陈旭. 温度影响下动力锂电池建模与均衡管理研究[D]. 长沙: 湖南大学, 2018.
[本文引用: 1]
CHEN X. Research on modeling and equalization management of power lithium battery under the influence of temperature[D]. Changsha: Hunan University, 2018.
[本文引用: 1]
[8]
康鑫, 时玮, 陈洪涛. 基于锂离子电池简化电化学模型的参数辨识[J]. 储能科学与技术, 2020, 9(3): 969-978.
[本文引用: 2]
KANG X, SHI W, CHEN H T. Parameter identification based on simplified electrochemical model of lithium ion battery[J]. Energy Storage Science and Technology, 2020, 9(3): 969-978.
[本文引用: 2]
[9]
陈洪涛. 锂电池电化学模型参数辨识研究[D]. 北京: 北京交通大学, 2019.
[本文引用: 1]
CHEN H T. Study on parameters identification of electrochemical model for lithium ion battery[D]. Beijing: Beijing Jiaotong University, 2019.
[本文引用: 1]
[10]
JAGUEMONT J, BOULON L, DUBÉ Y. A comprehensive review of lithium-ion batteries used in hybrid and electric vehicles at cold temperatures[J]. Applied Energy, 2016, 164: 99-114.
[本文引用: 1]
[11]
HARLOW J E, GLAZIER S L, LI J, et al. Use of asymmetric average charge- and average discharge- voltages as an indicator of the onset of unwanted lithium deposition in lithium-ion cells[J]. Journal of the Electrochemical Society, 2018, 165(16): A3595-A3601.
[本文引用: 1]
[12]
WANG D F, HUANG H Q, TANG Z H, et al. A lithium-ion battery electrochemical-thermal model for a wide temperature range applications[J]. Electrochimica Acta, 2020, 362: 137118.
[本文引用: 1]
[13]
皇甫海文, 韩艾呈. 锂电池等效模型建立与参数辨识方法研究[J]. 电气开关, 2020, 58(3): 37-41.
[本文引用: 1]
HUANGPU Haiwen, HAN Aicheng. Research on lithium-ion battery models and model parameter identification methods[J]. Electric Switchgear, 2020, 58(3): 37-41.
[本文引用: 1]
[14]
THAKKAR R R, RAO Y S, R SAWANT R. Performance analysis of electrical equivalent circuit models of lithium-ion battery[C]//2020 IEEE Pune Section International Conference (PuneCon). December 16-18, 2020 , Pune, India. IEEE, 2020: 103-107.
[本文引用: 1]
[15]
何耀, 刘兴涛, 张陈斌, 等. 基于动力电池组内阻模型的绝缘检测算法[J]. 吉林大学学报(工学版), 2013, 43(5): 1165-1170.
[本文引用: 1]
HE Y, LIU X T, ZHANG C B, et al. Insulation detection algorithm for high-power battery system based on internal resistance model[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(5): 1165-1170.
[本文引用: 1]
[16]
杨杰, 王婷, 杜春雨, 等. 锂离子电池模型研究综述[J]. 储能科学与技术, 2019, 8(1): 58-64.
[本文引用: 1]
YANG J, WANG T, DU C Y, et al. Overview of the modeling of lithium-ion batteries[J]. Energy Storage Science and Technology, 2019, 8(1): 58-64.
[本文引用: 1]
[17]
魏克新, 陈峭岩. 基于多模型自适应卡尔曼滤波器的电动汽车电池荷电状态估计[J]. 中国电机工程学报, 2012, 32(31): 19-26,214.
[本文引用: 1]
WEI K X, CHEN Q Y. Electric vehicle battery SOC estimation based on multiple-model adaptive Kalman filter[J]. Proceedings of the CSEE, 2012, 32(31): 19-26, 214.
[本文引用: 1]
[18]
HUANG K F, WANG Y, FENG J Q. Research on equivalent circuit Model of Lithium-ion battery for electric vehicles[C]//2020 3rd World Conference on Mechanical Engineering and Intelligent Manufacturing (WCMEIM). December 4-6, 2020 , Shanghai, China. IEEE, 2020: 492-496.
[本文引用: 1]
[19]
张宾, 郭连兑, 李宏义, 等. 电动汽车用磷酸铁锂离子电池的PNGV模型分析[J]. 电源技术, 2009, 33(5): 417-421.
[本文引用: 1]
ZHANG B, GUO L D, LI H Y, et al. PNGV model analysis of LiFePO4 Li-ion battery for electric vehicle[J]. Chinese Journal of Power Sources, 2009, 33(5): 417-421.
[本文引用: 1]
[20]
CHEN S J, ZHAO Z D. Modeling and simulation of a new ternary lithium battery based on the 2th-order equivalent circuit model[C]//2019 International Conference on Intelligent Computing, Automation and Systems (ICICAS). December 6-8, 2019 , Chongqing, China. IEEE, 2019: 402-405.
[本文引用: 1]
[21]
HE D W, ZHANG W, LUO X Y. Overview of power lithium battery modeling and soc estimation[J]. IOP Conference Series: Earth and Environmental Science, 2020, 461(1): 012032.
[本文引用: 1]
[22]
吴小慧, 张兴敢. 锂电池二阶RC等效电路模型参数辨识[J]. 南京大学学报(自然科学), 2020, 56(5): 754-761.
[本文引用: 1]
WU X H, ZHANG X G. Parameters identification of second order RC equivalent circuit model for lithium batteries[J]. Journal of Nanjing University (Natural Science), 2020, 56(5): 754-761.
[本文引用: 1]
[23]
林成涛, 仇斌, 陈全世. 电动汽车电池功率输入等效电路模型的比较研究[J]. 汽车工程, 2006, 28(3): 229-234.
[本文引用: 1]
LIN C T, QIU B, CHEN Q S. A comparative study on power input equivalent circuit model for electric vehicle battery[J]. Automotive Engineering, 2006, 28(3): 229-234.
[本文引用: 1]
[24]
RAHIMI EICHI H, CHOW M Y. Modeling and analysis of battery hysteresis effects[C]//2012 IEEE Energy Conversion Congress and Exposition (ECCE). September 15-20, 2012 , Raleigh, NC, USA. IEEE, 2012: 4479-4486.
[本文引用: 1]
[25]
李建杰. 电动汽车动力锂电池建模、仿真及均衡控制研究[D]. 郑州: 郑州大学, 2020.
[本文引用: 1]
LI J J. Research on modeling, simulation and equalization control for power lithium battery of electric vehicle[D]. Zhengzhou: Zhengzhou University, 2020.
[本文引用: 1]
[26]
黄凯, 郭永芳, 李志刚. 考虑迟滞效应影响的动力锂离子电池特性建模[J]. 电网技术, 2017, 41(8): 2695-2702.
[本文引用: 1]
HUANG K, GUO Y F, LI Z G. Modeling of power lithium-ion battery behavior considering hysteresis effect[J]. Power System Technology, 2017, 41(8): 2695-2702.
[本文引用: 1]
[27]
KIM T, QIAO W, QU L. Hysteresis modeling for model-based condition monitoring of lithium-ion batteries[C]//2015 IEEE Energy Conversion Congress and Exposition (ECCE). September 20-24, 2015 , Montreal, QC, Canada. IEEE, 2015: 5068-5073.
[本文引用: 1]
[28]
宋凯, 陈旭, 成艾国. 考虑温度影响和滞回效应的锂电池特性建模[J]. 汽车工程, 2019, 41(3): 334-339.
[本文引用: 1]
SONG K, CHEN X, CHENG A G. Modeling of lithium battery characteristics considering the influence of temperature and hysteresis effect[J]. Automotive Engineering, 2019, 41(3): 334-339.
[本文引用: 1]
[29]
户龙辉, 李欣然, 黄际元, 等. 考虑多因素的磷酸铁锂电池综合建模研究[J]. 电源技术, 2016, 40(3): 514-518.
[本文引用: 1]
HU L H, LI X R, HUANG J Y, et al. Various factors LiFePO4 battery modeling study consideration[J]. Chinese Journal of Power Sources, 2016, 40(3): 514-518.
[本文引用: 1]
[30]
KHARISMA M D, RIDWAN M, ILMIAWAN A F, et al. Modeling and simulation of lithium-ion battery pack using modified battery cell model[C]//2019 6th International Conference on Electric Vehicular Technology (ICEVT). November 18-21, 2019 , Bali, Indonesia. IEEE, 2019: 25-30.
[本文引用: 1]
[31]
宋旬. 电动汽车串并联动力电池组建模与性能分析研究[D]. 西安: 长安大学, 2019.
[本文引用: 1]
SONG X. Study on modeling and performance analysis of series-parallel connected battery pack for electric vehicles[D]. Xi'an: Changan University, 2019.
[本文引用: 1]
[32]
李建林, 屈树慷, 黄孟阳, 等. 锂离子电池建模现状研究综述[J]. 热力发电, 2021, 50(7): 1-7.
[本文引用: 1]
LI J L, QU S K, HUANG M Y, et al. A review of current research on lithium-ion battery modeling[J]. Thermal Power Generation, 2021, 50(7): 1-7.
[本文引用: 1]
[33]
张加林. 动力电池主动均衡系统关键技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2018.
[本文引用: 1]
ZHANG J L. Research on key technologies of active battery balance system[D]. Harbin: Harbin Institute of Technology, 2018.
[本文引用: 1]
[34]
杜浩. 电动汽车电池组的均衡管理系统设计[D]. 新乡: 河南师范大学, 2017.
[本文引用: 1]
DU H. The design of the equalization management system of electric vehicle battery[D]. Xinxiang, China: Henan Normal University, 2017.
[本文引用: 1]
[35]
李腾, 林成涛, 陈全世. 磷酸铁锂电池组成组过程的不一致性分析[J]. 清华大学学报(自然科学版), 2012, 52(7): 1001-1006.
[本文引用: 1]
LI T, LIN C T, CHEN Q S. Inconsistency analysis of LiFePO4 battery packing[J]. Journal of Tsinghua University (Science and Technology), 2012, 52(7): 1001-1006.
[本文引用: 1]
[36]
张维戈, 时玮, 姜久春, 等. 动力锂离子电池串并联仿真技术研究[J]. 电网技术, 2012, 36(10): 70-75.
[本文引用: 1]
ZHANG W G, SHI W, JIANG J C, et al. Numerical simulation technique of series-parallel power lithium ion battery[J]. Power System Technology, 2012, 36(10): 70-75.
[本文引用: 1]
[37]
张言茹. 动力锂离子电池并联衰退机理分析[D]. 北京: 北京交通大学, 2015.
[本文引用: 1]
ZHANG Y R. Analysis of fading mechanisms for parallel-connected power lithium-ion batteries[D]. Beijing: Beijing Jiaotong University, 2015.
[本文引用: 1]
[38]
范刘洋, 汪可友, 张宝群, 等. 考虑电池组不一致性的储能系统建模及仿真[J]. 电力系统自动化, 2016, 40(3): 110-115.
[本文引用: 1]
FAN L Y, WANG K Y, ZHANG B Q, et al. Modeling and simulation of battery energy storage system considering intrinsic inconsistency[J]. Automation of Electric Power Systems, 2016, 40(3): 110-115.
[本文引用: 1]
[39]
苏振浩, 李晓杰, 秦晋, 等. 基于BP人工神经网络的动力电池SOC估算方法[J]. 储能科学与技术, 2019, 8(5): 868-873.
[本文引用: 1]
SU Z H, LI X J, QIN J, et al. SOC estimation method of power battery based on BP artificial neural network[J]. Energy Storage Science and Technology, 2019, 8(5): 868-873.
[本文引用: 1]
[40]
WANG P, FAN J, OU Y, et al. A comparative study of machine learning based modeling methods for Lithium-ion battery[J]. IOP Conference Series: Earth and Environmental Science, 2020, 546(5): 052045.
[本文引用: 1]
[41]
WEI Y, LING L Y. State of charge estimation for lithium-ion battery based on artificial neural network[C]//2021 IEEE 5th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC). March 12-14, 2021 , Chongqing, China. IEEE, 2021: 2454-2458.
[本文引用: 1]
[42]
黄妙华, 严永刚, 朱立明. 改进BP神经网络的磷酸铁锂电池SOC估算[J]. 武汉理工大学学报(信息与管理工程版), 2014, 36(6): 790-793.
[本文引用: 2]
HUANG M H, YAN Y G, ZHU L M. SOC estimation of lithium iron phosphate battery based on improved BP neural network[J]. Journal of Wuhan University of Technology (Information & Management Engineering), 2014, 36(6): 790-793.
[本文引用: 2]
[43]
胡晓松, 唐小林. 电动车辆锂离子动力电池建模方法综述[J]. 机械工程学报, 2017, 53(16): 20-31.
[本文引用: 1]
HU X S, TANG X L. Review of modeling techniques for lithium-ion traction batteries in electric vehicles[J]. Journal of Mechanical Engineering, 2017, 53(16): 20-31.
[本文引用: 1]
[44]
杨云龙. 基于改进型神经网络动力电池SOC估计研究[D]. 成都: 电子科技大学, 2019.
[本文引用: 1]
YANG Y L. Research on SOC estimation of power battery based on improved neural network[D]. Chengdu: University of Electronic Science and Technology of China, 2019.
[本文引用: 1]
[45]
徐峰. 基于改进神经网络模型的锂电池SOC预测方法研究[D]. 重庆: 重庆邮电大学, 2018.
[本文引用: 1]
XU F. Research on the prediction of lithium battery SOC based on improved artificial neural network model[D]. Chongqing: Chongqing University of Posts and Telecommunications, 2018.
[本文引用: 1]
1
... 由于化石燃料的燃烧对环境有所破坏,秉承可持续发展的理念,我国加大对太阳能、风能在内的清洁能源的开发利用.到2030年,我国使用的清洁能源比例将达25%,风光发电机组总容量将达12亿千瓦以上[1 ] ,且在2021年3月明确指出要建设主体为清洁能源的新型电力系统[2 ] .但是由于新能源发电不稳定,其发出的电能将对电网的电能质量造成冲击[3 ] .为了解决这个问题,在电网中加入储能单元,起到跟踪负荷曲线、平抑波动、提高电能质量的作用[4 ] .在双向功率转换器和能量管理系统都比较成熟的前提下,实现将其转化为大规模工程使用的重点在于建立精确、可靠的电池模型[5 ] .锂离子电池因为性能稳定,耐用性好,污染小、充电速度快被人们广泛利用[6 ] .本文将对锂离子电池常见的建模方法进行归纳,并对锂离子电池未来建模方向提出建议. ...
1
... 由于化石燃料的燃烧对环境有所破坏,秉承可持续发展的理念,我国加大对太阳能、风能在内的清洁能源的开发利用.到2030年,我国使用的清洁能源比例将达25%,风光发电机组总容量将达12亿千瓦以上[1 ] ,且在2021年3月明确指出要建设主体为清洁能源的新型电力系统[2 ] .但是由于新能源发电不稳定,其发出的电能将对电网的电能质量造成冲击[3 ] .为了解决这个问题,在电网中加入储能单元,起到跟踪负荷曲线、平抑波动、提高电能质量的作用[4 ] .在双向功率转换器和能量管理系统都比较成熟的前提下,实现将其转化为大规模工程使用的重点在于建立精确、可靠的电池模型[5 ] .锂离子电池因为性能稳定,耐用性好,污染小、充电速度快被人们广泛利用[6 ] .本文将对锂离子电池常见的建模方法进行归纳,并对锂离子电池未来建模方向提出建议. ...
1
... 由于化石燃料的燃烧对环境有所破坏,秉承可持续发展的理念,我国加大对太阳能、风能在内的清洁能源的开发利用.到2030年,我国使用的清洁能源比例将达25%,风光发电机组总容量将达12亿千瓦以上[1 ] ,且在2021年3月明确指出要建设主体为清洁能源的新型电力系统[2 ] .但是由于新能源发电不稳定,其发出的电能将对电网的电能质量造成冲击[3 ] .为了解决这个问题,在电网中加入储能单元,起到跟踪负荷曲线、平抑波动、提高电能质量的作用[4 ] .在双向功率转换器和能量管理系统都比较成熟的前提下,实现将其转化为大规模工程使用的重点在于建立精确、可靠的电池模型[5 ] .锂离子电池因为性能稳定,耐用性好,污染小、充电速度快被人们广泛利用[6 ] .本文将对锂离子电池常见的建模方法进行归纳,并对锂离子电池未来建模方向提出建议. ...
1
... 由于化石燃料的燃烧对环境有所破坏,秉承可持续发展的理念,我国加大对太阳能、风能在内的清洁能源的开发利用.到2030年,我国使用的清洁能源比例将达25%,风光发电机组总容量将达12亿千瓦以上[1 ] ,且在2021年3月明确指出要建设主体为清洁能源的新型电力系统[2 ] .但是由于新能源发电不稳定,其发出的电能将对电网的电能质量造成冲击[3 ] .为了解决这个问题,在电网中加入储能单元,起到跟踪负荷曲线、平抑波动、提高电能质量的作用[4 ] .在双向功率转换器和能量管理系统都比较成熟的前提下,实现将其转化为大规模工程使用的重点在于建立精确、可靠的电池模型[5 ] .锂离子电池因为性能稳定,耐用性好,污染小、充电速度快被人们广泛利用[6 ] .本文将对锂离子电池常见的建模方法进行归纳,并对锂离子电池未来建模方向提出建议. ...
1
... 由于化石燃料的燃烧对环境有所破坏,秉承可持续发展的理念,我国加大对太阳能、风能在内的清洁能源的开发利用.到2030年,我国使用的清洁能源比例将达25%,风光发电机组总容量将达12亿千瓦以上[1 ] ,且在2021年3月明确指出要建设主体为清洁能源的新型电力系统[2 ] .但是由于新能源发电不稳定,其发出的电能将对电网的电能质量造成冲击[3 ] .为了解决这个问题,在电网中加入储能单元,起到跟踪负荷曲线、平抑波动、提高电能质量的作用[4 ] .在双向功率转换器和能量管理系统都比较成熟的前提下,实现将其转化为大规模工程使用的重点在于建立精确、可靠的电池模型[5 ] .锂离子电池因为性能稳定,耐用性好,污染小、充电速度快被人们广泛利用[6 ] .本文将对锂离子电池常见的建模方法进行归纳,并对锂离子电池未来建模方向提出建议. ...
1
... 由于化石燃料的燃烧对环境有所破坏,秉承可持续发展的理念,我国加大对太阳能、风能在内的清洁能源的开发利用.到2030年,我国使用的清洁能源比例将达25%,风光发电机组总容量将达12亿千瓦以上[1 ] ,且在2021年3月明确指出要建设主体为清洁能源的新型电力系统[2 ] .但是由于新能源发电不稳定,其发出的电能将对电网的电能质量造成冲击[3 ] .为了解决这个问题,在电网中加入储能单元,起到跟踪负荷曲线、平抑波动、提高电能质量的作用[4 ] .在双向功率转换器和能量管理系统都比较成熟的前提下,实现将其转化为大规模工程使用的重点在于建立精确、可靠的电池模型[5 ] .锂离子电池因为性能稳定,耐用性好,污染小、充电速度快被人们广泛利用[6 ] .本文将对锂离子电池常见的建模方法进行归纳,并对锂离子电池未来建模方向提出建议. ...
1
... 由于化石燃料的燃烧对环境有所破坏,秉承可持续发展的理念,我国加大对太阳能、风能在内的清洁能源的开发利用.到2030年,我国使用的清洁能源比例将达25%,风光发电机组总容量将达12亿千瓦以上[1 ] ,且在2021年3月明确指出要建设主体为清洁能源的新型电力系统[2 ] .但是由于新能源发电不稳定,其发出的电能将对电网的电能质量造成冲击[3 ] .为了解决这个问题,在电网中加入储能单元,起到跟踪负荷曲线、平抑波动、提高电能质量的作用[4 ] .在双向功率转换器和能量管理系统都比较成熟的前提下,实现将其转化为大规模工程使用的重点在于建立精确、可靠的电池模型[5 ] .锂离子电池因为性能稳定,耐用性好,污染小、充电速度快被人们广泛利用[6 ] .本文将对锂离子电池常见的建模方法进行归纳,并对锂离子电池未来建模方向提出建议. ...
1
... 由于化石燃料的燃烧对环境有所破坏,秉承可持续发展的理念,我国加大对太阳能、风能在内的清洁能源的开发利用.到2030年,我国使用的清洁能源比例将达25%,风光发电机组总容量将达12亿千瓦以上[1 ] ,且在2021年3月明确指出要建设主体为清洁能源的新型电力系统[2 ] .但是由于新能源发电不稳定,其发出的电能将对电网的电能质量造成冲击[3 ] .为了解决这个问题,在电网中加入储能单元,起到跟踪负荷曲线、平抑波动、提高电能质量的作用[4 ] .在双向功率转换器和能量管理系统都比较成熟的前提下,实现将其转化为大规模工程使用的重点在于建立精确、可靠的电池模型[5 ] .锂离子电池因为性能稳定,耐用性好,污染小、充电速度快被人们广泛利用[6 ] .本文将对锂离子电池常见的建模方法进行归纳,并对锂离子电池未来建模方向提出建议. ...
1
... 由于化石燃料的燃烧对环境有所破坏,秉承可持续发展的理念,我国加大对太阳能、风能在内的清洁能源的开发利用.到2030年,我国使用的清洁能源比例将达25%,风光发电机组总容量将达12亿千瓦以上[1 ] ,且在2021年3月明确指出要建设主体为清洁能源的新型电力系统[2 ] .但是由于新能源发电不稳定,其发出的电能将对电网的电能质量造成冲击[3 ] .为了解决这个问题,在电网中加入储能单元,起到跟踪负荷曲线、平抑波动、提高电能质量的作用[4 ] .在双向功率转换器和能量管理系统都比较成熟的前提下,实现将其转化为大规模工程使用的重点在于建立精确、可靠的电池模型[5 ] .锂离子电池因为性能稳定,耐用性好,污染小、充电速度快被人们广泛利用[6 ] .本文将对锂离子电池常见的建模方法进行归纳,并对锂离子电池未来建模方向提出建议. ...
1
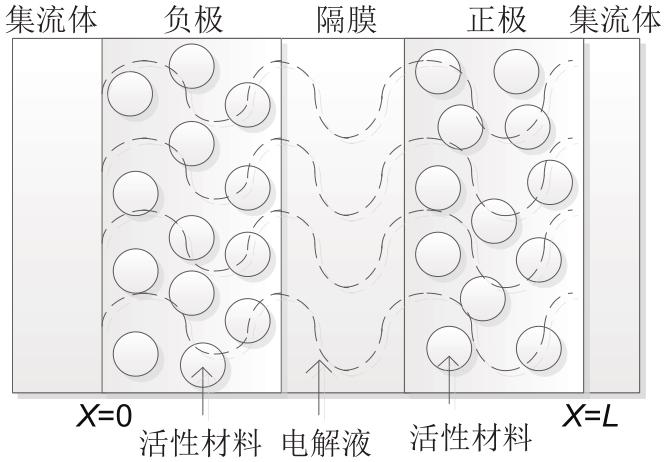
... 电化学模型是通过模拟电池电化学反应过程建立起来的模型,可以对电池外特性仿真且具有较高精确度.虽然电化学模型的描述方程比较复杂,但是由于其通过研究正负极材料、结构、尺寸对电池容量、电压的影响,可以对电池的研发提供参考,所以电化学模型常用于电池原理的分析和电池的研发[7 ] . ...
1
... 电化学模型是通过模拟电池电化学反应过程建立起来的模型,可以对电池外特性仿真且具有较高精确度.虽然电化学模型的描述方程比较复杂,但是由于其通过研究正负极材料、结构、尺寸对电池容量、电压的影响,可以对电池的研发提供参考,所以电化学模型常用于电池原理的分析和电池的研发[7 ] . ...
2
... 准二维电化学模型是应用较广泛的一种电化学模型,其对电池特性有较准确的描述,但是方程比较复杂.单粒子模型对准二维电化学模型进行大量简化,是最简单的电化学模型,但是其精度较低,尤其是在通过大电流时误差较大[8 ] ,也不太适合工程应用.目前对于锂离子电池电化学模型的研究主要是对准二维电化学模型进行适当的简化,并将多方面可能对电池有影响的因素考虑到锂电池建模中.如文献[8 -9 ]简化了固溶扩散的控制方程,考虑液相浓度、电势引起的过电势,并将变化的锂离子流量密度改为平均体积电流密度,简化后的模型降低了复杂性,具有一定的工程应用价值.由于在低温下锂离子在阳极沉淀,参与反应的锂离子数量的下降将直接导致电池可用容量的下降[10 -11 ] ,所以温度也是锂离子建模时需要考虑的重要因素之一,而上述文献缺少对温度的分析.文献[12 ]考虑了电池反应过程中温度对模型参数的影响,形成了电化学-热模型,从而更精确地描述电池的特性.综上所述,目前对电化学模型的研究主要是考虑多方面因素平衡电化学模型的实用性和精确度.建议未来通过对电化学模型不同电极材料、结构的仿真研究与创新,优化电化学模型数据,对电池设计研发提供参考. ...
... ,也不太适合工程应用.目前对于锂离子电池电化学模型的研究主要是对准二维电化学模型进行适当的简化,并将多方面可能对电池有影响的因素考虑到锂电池建模中.如文献[8 -9 ]简化了固溶扩散的控制方程,考虑液相浓度、电势引起的过电势,并将变化的锂离子流量密度改为平均体积电流密度,简化后的模型降低了复杂性,具有一定的工程应用价值.由于在低温下锂离子在阳极沉淀,参与反应的锂离子数量的下降将直接导致电池可用容量的下降[10 -11 ] ,所以温度也是锂离子建模时需要考虑的重要因素之一,而上述文献缺少对温度的分析.文献[12 ]考虑了电池反应过程中温度对模型参数的影响,形成了电化学-热模型,从而更精确地描述电池的特性.综上所述,目前对电化学模型的研究主要是考虑多方面因素平衡电化学模型的实用性和精确度.建议未来通过对电化学模型不同电极材料、结构的仿真研究与创新,优化电化学模型数据,对电池设计研发提供参考. ...
2
... 准二维电化学模型是应用较广泛的一种电化学模型,其对电池特性有较准确的描述,但是方程比较复杂.单粒子模型对准二维电化学模型进行大量简化,是最简单的电化学模型,但是其精度较低,尤其是在通过大电流时误差较大[8 ] ,也不太适合工程应用.目前对于锂离子电池电化学模型的研究主要是对准二维电化学模型进行适当的简化,并将多方面可能对电池有影响的因素考虑到锂电池建模中.如文献[8 -9 ]简化了固溶扩散的控制方程,考虑液相浓度、电势引起的过电势,并将变化的锂离子流量密度改为平均体积电流密度,简化后的模型降低了复杂性,具有一定的工程应用价值.由于在低温下锂离子在阳极沉淀,参与反应的锂离子数量的下降将直接导致电池可用容量的下降[10 -11 ] ,所以温度也是锂离子建模时需要考虑的重要因素之一,而上述文献缺少对温度的分析.文献[12 ]考虑了电池反应过程中温度对模型参数的影响,形成了电化学-热模型,从而更精确地描述电池的特性.综上所述,目前对电化学模型的研究主要是考虑多方面因素平衡电化学模型的实用性和精确度.建议未来通过对电化学模型不同电极材料、结构的仿真研究与创新,优化电化学模型数据,对电池设计研发提供参考. ...
... ,也不太适合工程应用.目前对于锂离子电池电化学模型的研究主要是对准二维电化学模型进行适当的简化,并将多方面可能对电池有影响的因素考虑到锂电池建模中.如文献[8 -9 ]简化了固溶扩散的控制方程,考虑液相浓度、电势引起的过电势,并将变化的锂离子流量密度改为平均体积电流密度,简化后的模型降低了复杂性,具有一定的工程应用价值.由于在低温下锂离子在阳极沉淀,参与反应的锂离子数量的下降将直接导致电池可用容量的下降[10 -11 ] ,所以温度也是锂离子建模时需要考虑的重要因素之一,而上述文献缺少对温度的分析.文献[12 ]考虑了电池反应过程中温度对模型参数的影响,形成了电化学-热模型,从而更精确地描述电池的特性.综上所述,目前对电化学模型的研究主要是考虑多方面因素平衡电化学模型的实用性和精确度.建议未来通过对电化学模型不同电极材料、结构的仿真研究与创新,优化电化学模型数据,对电池设计研发提供参考. ...
1
... 准二维电化学模型是应用较广泛的一种电化学模型,其对电池特性有较准确的描述,但是方程比较复杂.单粒子模型对准二维电化学模型进行大量简化,是最简单的电化学模型,但是其精度较低,尤其是在通过大电流时误差较大[8 ] ,也不太适合工程应用.目前对于锂离子电池电化学模型的研究主要是对准二维电化学模型进行适当的简化,并将多方面可能对电池有影响的因素考虑到锂电池建模中.如文献[8 -9 ]简化了固溶扩散的控制方程,考虑液相浓度、电势引起的过电势,并将变化的锂离子流量密度改为平均体积电流密度,简化后的模型降低了复杂性,具有一定的工程应用价值.由于在低温下锂离子在阳极沉淀,参与反应的锂离子数量的下降将直接导致电池可用容量的下降[10 -11 ] ,所以温度也是锂离子建模时需要考虑的重要因素之一,而上述文献缺少对温度的分析.文献[12 ]考虑了电池反应过程中温度对模型参数的影响,形成了电化学-热模型,从而更精确地描述电池的特性.综上所述,目前对电化学模型的研究主要是考虑多方面因素平衡电化学模型的实用性和精确度.建议未来通过对电化学模型不同电极材料、结构的仿真研究与创新,优化电化学模型数据,对电池设计研发提供参考. ...
1
... 准二维电化学模型是应用较广泛的一种电化学模型,其对电池特性有较准确的描述,但是方程比较复杂.单粒子模型对准二维电化学模型进行大量简化,是最简单的电化学模型,但是其精度较低,尤其是在通过大电流时误差较大[8 ] ,也不太适合工程应用.目前对于锂离子电池电化学模型的研究主要是对准二维电化学模型进行适当的简化,并将多方面可能对电池有影响的因素考虑到锂电池建模中.如文献[8 -9 ]简化了固溶扩散的控制方程,考虑液相浓度、电势引起的过电势,并将变化的锂离子流量密度改为平均体积电流密度,简化后的模型降低了复杂性,具有一定的工程应用价值.由于在低温下锂离子在阳极沉淀,参与反应的锂离子数量的下降将直接导致电池可用容量的下降[10 -11 ] ,所以温度也是锂离子建模时需要考虑的重要因素之一,而上述文献缺少对温度的分析.文献[12 ]考虑了电池反应过程中温度对模型参数的影响,形成了电化学-热模型,从而更精确地描述电池的特性.综上所述,目前对电化学模型的研究主要是考虑多方面因素平衡电化学模型的实用性和精确度.建议未来通过对电化学模型不同电极材料、结构的仿真研究与创新,优化电化学模型数据,对电池设计研发提供参考. ...
1
... 准二维电化学模型是应用较广泛的一种电化学模型,其对电池特性有较准确的描述,但是方程比较复杂.单粒子模型对准二维电化学模型进行大量简化,是最简单的电化学模型,但是其精度较低,尤其是在通过大电流时误差较大[8 ] ,也不太适合工程应用.目前对于锂离子电池电化学模型的研究主要是对准二维电化学模型进行适当的简化,并将多方面可能对电池有影响的因素考虑到锂电池建模中.如文献[8 -9 ]简化了固溶扩散的控制方程,考虑液相浓度、电势引起的过电势,并将变化的锂离子流量密度改为平均体积电流密度,简化后的模型降低了复杂性,具有一定的工程应用价值.由于在低温下锂离子在阳极沉淀,参与反应的锂离子数量的下降将直接导致电池可用容量的下降[10 -11 ] ,所以温度也是锂离子建模时需要考虑的重要因素之一,而上述文献缺少对温度的分析.文献[12 ]考虑了电池反应过程中温度对模型参数的影响,形成了电化学-热模型,从而更精确地描述电池的特性.综上所述,目前对电化学模型的研究主要是考虑多方面因素平衡电化学模型的实用性和精确度.建议未来通过对电化学模型不同电极材料、结构的仿真研究与创新,优化电化学模型数据,对电池设计研发提供参考. ...
1
... 准二维电化学模型是应用较广泛的一种电化学模型,其对电池特性有较准确的描述,但是方程比较复杂.单粒子模型对准二维电化学模型进行大量简化,是最简单的电化学模型,但是其精度较低,尤其是在通过大电流时误差较大[8 ] ,也不太适合工程应用.目前对于锂离子电池电化学模型的研究主要是对准二维电化学模型进行适当的简化,并将多方面可能对电池有影响的因素考虑到锂电池建模中.如文献[8 -9 ]简化了固溶扩散的控制方程,考虑液相浓度、电势引起的过电势,并将变化的锂离子流量密度改为平均体积电流密度,简化后的模型降低了复杂性,具有一定的工程应用价值.由于在低温下锂离子在阳极沉淀,参与反应的锂离子数量的下降将直接导致电池可用容量的下降[10 -11 ] ,所以温度也是锂离子建模时需要考虑的重要因素之一,而上述文献缺少对温度的分析.文献[12 ]考虑了电池反应过程中温度对模型参数的影响,形成了电化学-热模型,从而更精确地描述电池的特性.综上所述,目前对电化学模型的研究主要是考虑多方面因素平衡电化学模型的实用性和精确度.建议未来通过对电化学模型不同电极材料、结构的仿真研究与创新,优化电化学模型数据,对电池设计研发提供参考. ...
1
... 准二维电化学模型是应用较广泛的一种电化学模型,其对电池特性有较准确的描述,但是方程比较复杂.单粒子模型对准二维电化学模型进行大量简化,是最简单的电化学模型,但是其精度较低,尤其是在通过大电流时误差较大[8 ] ,也不太适合工程应用.目前对于锂离子电池电化学模型的研究主要是对准二维电化学模型进行适当的简化,并将多方面可能对电池有影响的因素考虑到锂电池建模中.如文献[8 -9 ]简化了固溶扩散的控制方程,考虑液相浓度、电势引起的过电势,并将变化的锂离子流量密度改为平均体积电流密度,简化后的模型降低了复杂性,具有一定的工程应用价值.由于在低温下锂离子在阳极沉淀,参与反应的锂离子数量的下降将直接导致电池可用容量的下降[10 -11 ] ,所以温度也是锂离子建模时需要考虑的重要因素之一,而上述文献缺少对温度的分析.文献[12 ]考虑了电池反应过程中温度对模型参数的影响,形成了电化学-热模型,从而更精确地描述电池的特性.综上所述,目前对电化学模型的研究主要是考虑多方面因素平衡电化学模型的实用性和精确度.建议未来通过对电化学模型不同电极材料、结构的仿真研究与创新,优化电化学模型数据,对电池设计研发提供参考. ...
1
... 等效电路模型是将电池的各种外特性通过电路元件之间的组合来表示的一种模型[13 ] .由于其清晰地给出了锂离子电池各元素与U-I 特性、荷电状态之间的数学关系,所以被广泛应用[14 ] .表1 把几种常用的电池模型进行了比较.其中,文献[15 ]的Rint模型由一个理想电压源和欧姆内阻构成.结构简单且参数容易计算,但是无法描述动态过程.当电池流过大电流时,其仿真误差增大,仿真精度大大降低[16 ] .所以一般仅仅用来描述理想电池,在实际应用中比较少.由于电池的电化学极化效应会改变电池电极的电势,文献[17 ]的Thevenin模型在上述基础上添加一个RC结构来模拟此效应,从而实现更高的精度.且其构造相对简单,可以实现大部分的电池仿真,在现实中的应用最广泛.但是受到老化和温度变化的影响较大,精确度一般[18 ] .文献[19 ]提出的PNGV模型比Thevenin模型多了一个电容C Q 20 -21 ]中介绍了由两组RC与一个电阻串联组成的二阶RC模型,其将浓差极化的影响也考虑在内,所以仿真精度较高,特性更接近真实的电池.但是随着元件的增多,结构也更加复杂,且未考虑温度的影响[22 ] .文献[23 ]中的GNL模型在二阶RC模型的基础上,增加了一个电阻R S
1
... 等效电路模型是将电池的各种外特性通过电路元件之间的组合来表示的一种模型[13 ] .由于其清晰地给出了锂离子电池各元素与U-I 特性、荷电状态之间的数学关系,所以被广泛应用[14 ] .表1 把几种常用的电池模型进行了比较.其中,文献[15 ]的Rint模型由一个理想电压源和欧姆内阻构成.结构简单且参数容易计算,但是无法描述动态过程.当电池流过大电流时,其仿真误差增大,仿真精度大大降低[16 ] .所以一般仅仅用来描述理想电池,在实际应用中比较少.由于电池的电化学极化效应会改变电池电极的电势,文献[17 ]的Thevenin模型在上述基础上添加一个RC结构来模拟此效应,从而实现更高的精度.且其构造相对简单,可以实现大部分的电池仿真,在现实中的应用最广泛.但是受到老化和温度变化的影响较大,精确度一般[18 ] .文献[19 ]提出的PNGV模型比Thevenin模型多了一个电容C Q 20 -21 ]中介绍了由两组RC与一个电阻串联组成的二阶RC模型,其将浓差极化的影响也考虑在内,所以仿真精度较高,特性更接近真实的电池.但是随着元件的增多,结构也更加复杂,且未考虑温度的影响[22 ] .文献[23 ]中的GNL模型在二阶RC模型的基础上,增加了一个电阻R S
1
... 等效电路模型是将电池的各种外特性通过电路元件之间的组合来表示的一种模型[13 ] .由于其清晰地给出了锂离子电池各元素与U-I 特性、荷电状态之间的数学关系,所以被广泛应用[14 ] .表1 把几种常用的电池模型进行了比较.其中,文献[15 ]的Rint模型由一个理想电压源和欧姆内阻构成.结构简单且参数容易计算,但是无法描述动态过程.当电池流过大电流时,其仿真误差增大,仿真精度大大降低[16 ] .所以一般仅仅用来描述理想电池,在实际应用中比较少.由于电池的电化学极化效应会改变电池电极的电势,文献[17 ]的Thevenin模型在上述基础上添加一个RC结构来模拟此效应,从而实现更高的精度.且其构造相对简单,可以实现大部分的电池仿真,在现实中的应用最广泛.但是受到老化和温度变化的影响较大,精确度一般[18 ] .文献[19 ]提出的PNGV模型比Thevenin模型多了一个电容C Q 20 -21 ]中介绍了由两组RC与一个电阻串联组成的二阶RC模型,其将浓差极化的影响也考虑在内,所以仿真精度较高,特性更接近真实的电池.但是随着元件的增多,结构也更加复杂,且未考虑温度的影响[22 ] .文献[23 ]中的GNL模型在二阶RC模型的基础上,增加了一个电阻R S
1
... 等效电路模型是将电池的各种外特性通过电路元件之间的组合来表示的一种模型[13 ] .由于其清晰地给出了锂离子电池各元素与U-I 特性、荷电状态之间的数学关系,所以被广泛应用[14 ] .表1 把几种常用的电池模型进行了比较.其中,文献[15 ]的Rint模型由一个理想电压源和欧姆内阻构成.结构简单且参数容易计算,但是无法描述动态过程.当电池流过大电流时,其仿真误差增大,仿真精度大大降低[16 ] .所以一般仅仅用来描述理想电池,在实际应用中比较少.由于电池的电化学极化效应会改变电池电极的电势,文献[17 ]的Thevenin模型在上述基础上添加一个RC结构来模拟此效应,从而实现更高的精度.且其构造相对简单,可以实现大部分的电池仿真,在现实中的应用最广泛.但是受到老化和温度变化的影响较大,精确度一般[18 ] .文献[19 ]提出的PNGV模型比Thevenin模型多了一个电容C Q 20 -21 ]中介绍了由两组RC与一个电阻串联组成的二阶RC模型,其将浓差极化的影响也考虑在内,所以仿真精度较高,特性更接近真实的电池.但是随着元件的增多,结构也更加复杂,且未考虑温度的影响[22 ] .文献[23 ]中的GNL模型在二阶RC模型的基础上,增加了一个电阻R S
1
... 等效电路模型是将电池的各种外特性通过电路元件之间的组合来表示的一种模型[13 ] .由于其清晰地给出了锂离子电池各元素与U-I 特性、荷电状态之间的数学关系,所以被广泛应用[14 ] .表1 把几种常用的电池模型进行了比较.其中,文献[15 ]的Rint模型由一个理想电压源和欧姆内阻构成.结构简单且参数容易计算,但是无法描述动态过程.当电池流过大电流时,其仿真误差增大,仿真精度大大降低[16 ] .所以一般仅仅用来描述理想电池,在实际应用中比较少.由于电池的电化学极化效应会改变电池电极的电势,文献[17 ]的Thevenin模型在上述基础上添加一个RC结构来模拟此效应,从而实现更高的精度.且其构造相对简单,可以实现大部分的电池仿真,在现实中的应用最广泛.但是受到老化和温度变化的影响较大,精确度一般[18 ] .文献[19 ]提出的PNGV模型比Thevenin模型多了一个电容C Q 20 -21 ]中介绍了由两组RC与一个电阻串联组成的二阶RC模型,其将浓差极化的影响也考虑在内,所以仿真精度较高,特性更接近真实的电池.但是随着元件的增多,结构也更加复杂,且未考虑温度的影响[22 ] .文献[23 ]中的GNL模型在二阶RC模型的基础上,增加了一个电阻R S
1
... 等效电路模型是将电池的各种外特性通过电路元件之间的组合来表示的一种模型[13 ] .由于其清晰地给出了锂离子电池各元素与U-I 特性、荷电状态之间的数学关系,所以被广泛应用[14 ] .表1 把几种常用的电池模型进行了比较.其中,文献[15 ]的Rint模型由一个理想电压源和欧姆内阻构成.结构简单且参数容易计算,但是无法描述动态过程.当电池流过大电流时,其仿真误差增大,仿真精度大大降低[16 ] .所以一般仅仅用来描述理想电池,在实际应用中比较少.由于电池的电化学极化效应会改变电池电极的电势,文献[17 ]的Thevenin模型在上述基础上添加一个RC结构来模拟此效应,从而实现更高的精度.且其构造相对简单,可以实现大部分的电池仿真,在现实中的应用最广泛.但是受到老化和温度变化的影响较大,精确度一般[18 ] .文献[19 ]提出的PNGV模型比Thevenin模型多了一个电容C Q 20 -21 ]中介绍了由两组RC与一个电阻串联组成的二阶RC模型,其将浓差极化的影响也考虑在内,所以仿真精度较高,特性更接近真实的电池.但是随着元件的增多,结构也更加复杂,且未考虑温度的影响[22 ] .文献[23 ]中的GNL模型在二阶RC模型的基础上,增加了一个电阻R S
1
... 等效电路模型是将电池的各种外特性通过电路元件之间的组合来表示的一种模型[13 ] .由于其清晰地给出了锂离子电池各元素与U-I 特性、荷电状态之间的数学关系,所以被广泛应用[14 ] .表1 把几种常用的电池模型进行了比较.其中,文献[15 ]的Rint模型由一个理想电压源和欧姆内阻构成.结构简单且参数容易计算,但是无法描述动态过程.当电池流过大电流时,其仿真误差增大,仿真精度大大降低[16 ] .所以一般仅仅用来描述理想电池,在实际应用中比较少.由于电池的电化学极化效应会改变电池电极的电势,文献[17 ]的Thevenin模型在上述基础上添加一个RC结构来模拟此效应,从而实现更高的精度.且其构造相对简单,可以实现大部分的电池仿真,在现实中的应用最广泛.但是受到老化和温度变化的影响较大,精确度一般[18 ] .文献[19 ]提出的PNGV模型比Thevenin模型多了一个电容C Q 20 -21 ]中介绍了由两组RC与一个电阻串联组成的二阶RC模型,其将浓差极化的影响也考虑在内,所以仿真精度较高,特性更接近真实的电池.但是随着元件的增多,结构也更加复杂,且未考虑温度的影响[22 ] .文献[23 ]中的GNL模型在二阶RC模型的基础上,增加了一个电阻R S
1
... 等效电路模型是将电池的各种外特性通过电路元件之间的组合来表示的一种模型[13 ] .由于其清晰地给出了锂离子电池各元素与U-I 特性、荷电状态之间的数学关系,所以被广泛应用[14 ] .表1 把几种常用的电池模型进行了比较.其中,文献[15 ]的Rint模型由一个理想电压源和欧姆内阻构成.结构简单且参数容易计算,但是无法描述动态过程.当电池流过大电流时,其仿真误差增大,仿真精度大大降低[16 ] .所以一般仅仅用来描述理想电池,在实际应用中比较少.由于电池的电化学极化效应会改变电池电极的电势,文献[17 ]的Thevenin模型在上述基础上添加一个RC结构来模拟此效应,从而实现更高的精度.且其构造相对简单,可以实现大部分的电池仿真,在现实中的应用最广泛.但是受到老化和温度变化的影响较大,精确度一般[18 ] .文献[19 ]提出的PNGV模型比Thevenin模型多了一个电容C Q 20 -21 ]中介绍了由两组RC与一个电阻串联组成的二阶RC模型,其将浓差极化的影响也考虑在内,所以仿真精度较高,特性更接近真实的电池.但是随着元件的增多,结构也更加复杂,且未考虑温度的影响[22 ] .文献[23 ]中的GNL模型在二阶RC模型的基础上,增加了一个电阻R S
1
... 等效电路模型是将电池的各种外特性通过电路元件之间的组合来表示的一种模型[13 ] .由于其清晰地给出了锂离子电池各元素与U-I 特性、荷电状态之间的数学关系,所以被广泛应用[14 ] .表1 把几种常用的电池模型进行了比较.其中,文献[15 ]的Rint模型由一个理想电压源和欧姆内阻构成.结构简单且参数容易计算,但是无法描述动态过程.当电池流过大电流时,其仿真误差增大,仿真精度大大降低[16 ] .所以一般仅仅用来描述理想电池,在实际应用中比较少.由于电池的电化学极化效应会改变电池电极的电势,文献[17 ]的Thevenin模型在上述基础上添加一个RC结构来模拟此效应,从而实现更高的精度.且其构造相对简单,可以实现大部分的电池仿真,在现实中的应用最广泛.但是受到老化和温度变化的影响较大,精确度一般[18 ] .文献[19 ]提出的PNGV模型比Thevenin模型多了一个电容C Q 20 -21 ]中介绍了由两组RC与一个电阻串联组成的二阶RC模型,其将浓差极化的影响也考虑在内,所以仿真精度较高,特性更接近真实的电池.但是随着元件的增多,结构也更加复杂,且未考虑温度的影响[22 ] .文献[23 ]中的GNL模型在二阶RC模型的基础上,增加了一个电阻R S
1
... 等效电路模型是将电池的各种外特性通过电路元件之间的组合来表示的一种模型[13 ] .由于其清晰地给出了锂离子电池各元素与U-I 特性、荷电状态之间的数学关系,所以被广泛应用[14 ] .表1 把几种常用的电池模型进行了比较.其中,文献[15 ]的Rint模型由一个理想电压源和欧姆内阻构成.结构简单且参数容易计算,但是无法描述动态过程.当电池流过大电流时,其仿真误差增大,仿真精度大大降低[16 ] .所以一般仅仅用来描述理想电池,在实际应用中比较少.由于电池的电化学极化效应会改变电池电极的电势,文献[17 ]的Thevenin模型在上述基础上添加一个RC结构来模拟此效应,从而实现更高的精度.且其构造相对简单,可以实现大部分的电池仿真,在现实中的应用最广泛.但是受到老化和温度变化的影响较大,精确度一般[18 ] .文献[19 ]提出的PNGV模型比Thevenin模型多了一个电容C Q 20 -21 ]中介绍了由两组RC与一个电阻串联组成的二阶RC模型,其将浓差极化的影响也考虑在内,所以仿真精度较高,特性更接近真实的电池.但是随着元件的增多,结构也更加复杂,且未考虑温度的影响[22 ] .文献[23 ]中的GNL模型在二阶RC模型的基础上,增加了一个电阻R S
1
... 等效电路模型是将电池的各种外特性通过电路元件之间的组合来表示的一种模型[13 ] .由于其清晰地给出了锂离子电池各元素与U-I 特性、荷电状态之间的数学关系,所以被广泛应用[14 ] .表1 把几种常用的电池模型进行了比较.其中,文献[15 ]的Rint模型由一个理想电压源和欧姆内阻构成.结构简单且参数容易计算,但是无法描述动态过程.当电池流过大电流时,其仿真误差增大,仿真精度大大降低[16 ] .所以一般仅仅用来描述理想电池,在实际应用中比较少.由于电池的电化学极化效应会改变电池电极的电势,文献[17 ]的Thevenin模型在上述基础上添加一个RC结构来模拟此效应,从而实现更高的精度.且其构造相对简单,可以实现大部分的电池仿真,在现实中的应用最广泛.但是受到老化和温度变化的影响较大,精确度一般[18 ] .文献[19 ]提出的PNGV模型比Thevenin模型多了一个电容C Q 20 -21 ]中介绍了由两组RC与一个电阻串联组成的二阶RC模型,其将浓差极化的影响也考虑在内,所以仿真精度较高,特性更接近真实的电池.但是随着元件的增多,结构也更加复杂,且未考虑温度的影响[22 ] .文献[23 ]中的GNL模型在二阶RC模型的基础上,增加了一个电阻R S
1
... 等效电路模型是将电池的各种外特性通过电路元件之间的组合来表示的一种模型[13 ] .由于其清晰地给出了锂离子电池各元素与U-I 特性、荷电状态之间的数学关系,所以被广泛应用[14 ] .表1 把几种常用的电池模型进行了比较.其中,文献[15 ]的Rint模型由一个理想电压源和欧姆内阻构成.结构简单且参数容易计算,但是无法描述动态过程.当电池流过大电流时,其仿真误差增大,仿真精度大大降低[16 ] .所以一般仅仅用来描述理想电池,在实际应用中比较少.由于电池的电化学极化效应会改变电池电极的电势,文献[17 ]的Thevenin模型在上述基础上添加一个RC结构来模拟此效应,从而实现更高的精度.且其构造相对简单,可以实现大部分的电池仿真,在现实中的应用最广泛.但是受到老化和温度变化的影响较大,精确度一般[18 ] .文献[19 ]提出的PNGV模型比Thevenin模型多了一个电容C Q 20 -21 ]中介绍了由两组RC与一个电阻串联组成的二阶RC模型,其将浓差极化的影响也考虑在内,所以仿真精度较高,特性更接近真实的电池.但是随着元件的增多,结构也更加复杂,且未考虑温度的影响[22 ] .文献[23 ]中的GNL模型在二阶RC模型的基础上,增加了一个电阻R S
1
... 等效电路模型是将电池的各种外特性通过电路元件之间的组合来表示的一种模型[13 ] .由于其清晰地给出了锂离子电池各元素与U-I 特性、荷电状态之间的数学关系,所以被广泛应用[14 ] .表1 把几种常用的电池模型进行了比较.其中,文献[15 ]的Rint模型由一个理想电压源和欧姆内阻构成.结构简单且参数容易计算,但是无法描述动态过程.当电池流过大电流时,其仿真误差增大,仿真精度大大降低[16 ] .所以一般仅仅用来描述理想电池,在实际应用中比较少.由于电池的电化学极化效应会改变电池电极的电势,文献[17 ]的Thevenin模型在上述基础上添加一个RC结构来模拟此效应,从而实现更高的精度.且其构造相对简单,可以实现大部分的电池仿真,在现实中的应用最广泛.但是受到老化和温度变化的影响较大,精确度一般[18 ] .文献[19 ]提出的PNGV模型比Thevenin模型多了一个电容C Q 20 -21 ]中介绍了由两组RC与一个电阻串联组成的二阶RC模型,其将浓差极化的影响也考虑在内,所以仿真精度较高,特性更接近真实的电池.但是随着元件的增多,结构也更加复杂,且未考虑温度的影响[22 ] .文献[23 ]中的GNL模型在二阶RC模型的基础上,增加了一个电阻R S
1
... 等效电路模型是将电池的各种外特性通过电路元件之间的组合来表示的一种模型[13 ] .由于其清晰地给出了锂离子电池各元素与U-I 特性、荷电状态之间的数学关系,所以被广泛应用[14 ] .表1 把几种常用的电池模型进行了比较.其中,文献[15 ]的Rint模型由一个理想电压源和欧姆内阻构成.结构简单且参数容易计算,但是无法描述动态过程.当电池流过大电流时,其仿真误差增大,仿真精度大大降低[16 ] .所以一般仅仅用来描述理想电池,在实际应用中比较少.由于电池的电化学极化效应会改变电池电极的电势,文献[17 ]的Thevenin模型在上述基础上添加一个RC结构来模拟此效应,从而实现更高的精度.且其构造相对简单,可以实现大部分的电池仿真,在现实中的应用最广泛.但是受到老化和温度变化的影响较大,精确度一般[18 ] .文献[19 ]提出的PNGV模型比Thevenin模型多了一个电容C Q 20 -21 ]中介绍了由两组RC与一个电阻串联组成的二阶RC模型,其将浓差极化的影响也考虑在内,所以仿真精度较高,特性更接近真实的电池.但是随着元件的增多,结构也更加复杂,且未考虑温度的影响[22 ] .文献[23 ]中的GNL模型在二阶RC模型的基础上,增加了一个电阻R S
1
... 等效电路模型是将电池的各种外特性通过电路元件之间的组合来表示的一种模型[13 ] .由于其清晰地给出了锂离子电池各元素与U-I 特性、荷电状态之间的数学关系,所以被广泛应用[14 ] .表1 把几种常用的电池模型进行了比较.其中,文献[15 ]的Rint模型由一个理想电压源和欧姆内阻构成.结构简单且参数容易计算,但是无法描述动态过程.当电池流过大电流时,其仿真误差增大,仿真精度大大降低[16 ] .所以一般仅仅用来描述理想电池,在实际应用中比较少.由于电池的电化学极化效应会改变电池电极的电势,文献[17 ]的Thevenin模型在上述基础上添加一个RC结构来模拟此效应,从而实现更高的精度.且其构造相对简单,可以实现大部分的电池仿真,在现实中的应用最广泛.但是受到老化和温度变化的影响较大,精确度一般[18 ] .文献[19 ]提出的PNGV模型比Thevenin模型多了一个电容C Q 20 -21 ]中介绍了由两组RC与一个电阻串联组成的二阶RC模型,其将浓差极化的影响也考虑在内,所以仿真精度较高,特性更接近真实的电池.但是随着元件的增多,结构也更加复杂,且未考虑温度的影响[22 ] .文献[23 ]中的GNL模型在二阶RC模型的基础上,增加了一个电阻R S
1
... 等效电路模型是将电池的各种外特性通过电路元件之间的组合来表示的一种模型[13 ] .由于其清晰地给出了锂离子电池各元素与U-I 特性、荷电状态之间的数学关系,所以被广泛应用[14 ] .表1 把几种常用的电池模型进行了比较.其中,文献[15 ]的Rint模型由一个理想电压源和欧姆内阻构成.结构简单且参数容易计算,但是无法描述动态过程.当电池流过大电流时,其仿真误差增大,仿真精度大大降低[16 ] .所以一般仅仅用来描述理想电池,在实际应用中比较少.由于电池的电化学极化效应会改变电池电极的电势,文献[17 ]的Thevenin模型在上述基础上添加一个RC结构来模拟此效应,从而实现更高的精度.且其构造相对简单,可以实现大部分的电池仿真,在现实中的应用最广泛.但是受到老化和温度变化的影响较大,精确度一般[18 ] .文献[19 ]提出的PNGV模型比Thevenin模型多了一个电容C Q 20 -21 ]中介绍了由两组RC与一个电阻串联组成的二阶RC模型,其将浓差极化的影响也考虑在内,所以仿真精度较高,特性更接近真实的电池.但是随着元件的增多,结构也更加复杂,且未考虑温度的影响[22 ] .文献[23 ]中的GNL模型在二阶RC模型的基础上,增加了一个电阻R S
1
... 等效电路模型是将电池的各种外特性通过电路元件之间的组合来表示的一种模型[13 ] .由于其清晰地给出了锂离子电池各元素与U-I 特性、荷电状态之间的数学关系,所以被广泛应用[14 ] .表1 把几种常用的电池模型进行了比较.其中,文献[15 ]的Rint模型由一个理想电压源和欧姆内阻构成.结构简单且参数容易计算,但是无法描述动态过程.当电池流过大电流时,其仿真误差增大,仿真精度大大降低[16 ] .所以一般仅仅用来描述理想电池,在实际应用中比较少.由于电池的电化学极化效应会改变电池电极的电势,文献[17 ]的Thevenin模型在上述基础上添加一个RC结构来模拟此效应,从而实现更高的精度.且其构造相对简单,可以实现大部分的电池仿真,在现实中的应用最广泛.但是受到老化和温度变化的影响较大,精确度一般[18 ] .文献[19 ]提出的PNGV模型比Thevenin模型多了一个电容C Q 20 -21 ]中介绍了由两组RC与一个电阻串联组成的二阶RC模型,其将浓差极化的影响也考虑在内,所以仿真精度较高,特性更接近真实的电池.但是随着元件的增多,结构也更加复杂,且未考虑温度的影响[22 ] .文献[23 ]中的GNL模型在二阶RC模型的基础上,增加了一个电阻R S
1
... 等效电路模型是将电池的各种外特性通过电路元件之间的组合来表示的一种模型[13 ] .由于其清晰地给出了锂离子电池各元素与U-I 特性、荷电状态之间的数学关系,所以被广泛应用[14 ] .表1 把几种常用的电池模型进行了比较.其中,文献[15 ]的Rint模型由一个理想电压源和欧姆内阻构成.结构简单且参数容易计算,但是无法描述动态过程.当电池流过大电流时,其仿真误差增大,仿真精度大大降低[16 ] .所以一般仅仅用来描述理想电池,在实际应用中比较少.由于电池的电化学极化效应会改变电池电极的电势,文献[17 ]的Thevenin模型在上述基础上添加一个RC结构来模拟此效应,从而实现更高的精度.且其构造相对简单,可以实现大部分的电池仿真,在现实中的应用最广泛.但是受到老化和温度变化的影响较大,精确度一般[18 ] .文献[19 ]提出的PNGV模型比Thevenin模型多了一个电容C Q 20 -21 ]中介绍了由两组RC与一个电阻串联组成的二阶RC模型,其将浓差极化的影响也考虑在内,所以仿真精度较高,特性更接近真实的电池.但是随着元件的增多,结构也更加复杂,且未考虑温度的影响[22 ] .文献[23 ]中的GNL模型在二阶RC模型的基础上,增加了一个电阻R S
1
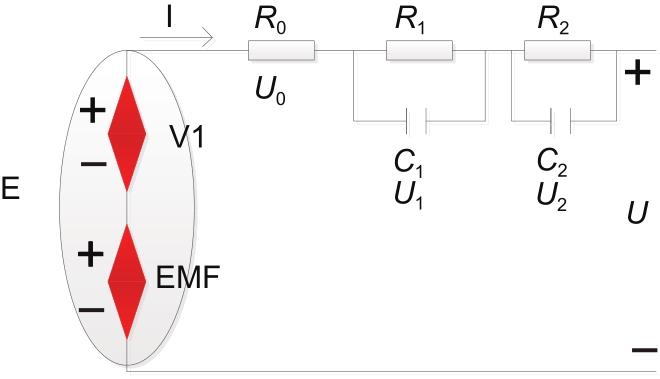
... 由于上述模型均存在一定不足,对电池状态的估计存在误差[24 ] ,所以需要建立考虑了电池的电动势特性和超电势特性的新模型来提高仿真精度.针对以上特点,文献[25 ]考虑了电池的电动势特性和超电势特性,通过加权处理充放电平衡电势,得到滞回电压V 1 E M F
1
... 由于上述模型均存在一定不足,对电池状态的估计存在误差[24 ] ,所以需要建立考虑了电池的电动势特性和超电势特性的新模型来提高仿真精度.针对以上特点,文献[25 ]考虑了电池的电动势特性和超电势特性,通过加权处理充放电平衡电势,得到滞回电压V 1 E M F
1
... 由于上述模型均存在一定不足,对电池状态的估计存在误差[24 ] ,所以需要建立考虑了电池的电动势特性和超电势特性的新模型来提高仿真精度.针对以上特点,文献[25 ]考虑了电池的电动势特性和超电势特性,通过加权处理充放电平衡电势,得到滞回电压V 1 E M F
1
... 这样改进的等效电路模型更接近锂离子电池真实工作情况,一定程度上提高了仿真精度,但是其对于电动势的修正值是不变的,并未考虑实际工况下迟滞电压值随SOC变化这一特性,所以精确度一般;文献[26 ]通过研究不同SOC对应的不同迟滞电压,将SOC分成5%~40%、40%~80%、80%~95%三个区间,并对应不同的迟滞电压值对模型进行修正,降低了模型的积累误差,对模型精度有较好的提升,但是没有考虑温度的影响;文献[27 ]将电池工作区间分为低SOC工作区间(SOC<20%)和高SOC工作区间(20%≤SOC≤100%),通过实验发现在低SOC工作区间时,温度对于SOC-OCV曲线的影响较大.且相较于高温环境,在低温环境下,不考虑迟滞效应将带来更大误差.文献[28 ]发现相同SOC时,最大滞回电压随着温度的升高而减小,从而建立了考虑温度影响的电池模型,通过模型验证使得其端电压输出误差减小50%,精度提高一倍;文献[29 ]建立了一个考虑容量衰减、自身温升、电池贮存等多因素影响的复杂锂电池模型,通过仿真验证了模型的精度.目前关于锂离子电池等效电路模型的研究主要是对其进行适当的改进,通过引入适合的电气元件,优化锂离子电池参数计算方法等途径,在更好提升锂离子电池等效电路模型建模精度的同时,也使其不至于过分复杂,从而更好地模拟锂电池真实工况. ...
1
... 这样改进的等效电路模型更接近锂离子电池真实工作情况,一定程度上提高了仿真精度,但是其对于电动势的修正值是不变的,并未考虑实际工况下迟滞电压值随SOC变化这一特性,所以精确度一般;文献[26 ]通过研究不同SOC对应的不同迟滞电压,将SOC分成5%~40%、40%~80%、80%~95%三个区间,并对应不同的迟滞电压值对模型进行修正,降低了模型的积累误差,对模型精度有较好的提升,但是没有考虑温度的影响;文献[27 ]将电池工作区间分为低SOC工作区间(SOC<20%)和高SOC工作区间(20%≤SOC≤100%),通过实验发现在低SOC工作区间时,温度对于SOC-OCV曲线的影响较大.且相较于高温环境,在低温环境下,不考虑迟滞效应将带来更大误差.文献[28 ]发现相同SOC时,最大滞回电压随着温度的升高而减小,从而建立了考虑温度影响的电池模型,通过模型验证使得其端电压输出误差减小50%,精度提高一倍;文献[29 ]建立了一个考虑容量衰减、自身温升、电池贮存等多因素影响的复杂锂电池模型,通过仿真验证了模型的精度.目前关于锂离子电池等效电路模型的研究主要是对其进行适当的改进,通过引入适合的电气元件,优化锂离子电池参数计算方法等途径,在更好提升锂离子电池等效电路模型建模精度的同时,也使其不至于过分复杂,从而更好地模拟锂电池真实工况. ...
1
... 这样改进的等效电路模型更接近锂离子电池真实工作情况,一定程度上提高了仿真精度,但是其对于电动势的修正值是不变的,并未考虑实际工况下迟滞电压值随SOC变化这一特性,所以精确度一般;文献[26 ]通过研究不同SOC对应的不同迟滞电压,将SOC分成5%~40%、40%~80%、80%~95%三个区间,并对应不同的迟滞电压值对模型进行修正,降低了模型的积累误差,对模型精度有较好的提升,但是没有考虑温度的影响;文献[27 ]将电池工作区间分为低SOC工作区间(SOC<20%)和高SOC工作区间(20%≤SOC≤100%),通过实验发现在低SOC工作区间时,温度对于SOC-OCV曲线的影响较大.且相较于高温环境,在低温环境下,不考虑迟滞效应将带来更大误差.文献[28 ]发现相同SOC时,最大滞回电压随着温度的升高而减小,从而建立了考虑温度影响的电池模型,通过模型验证使得其端电压输出误差减小50%,精度提高一倍;文献[29 ]建立了一个考虑容量衰减、自身温升、电池贮存等多因素影响的复杂锂电池模型,通过仿真验证了模型的精度.目前关于锂离子电池等效电路模型的研究主要是对其进行适当的改进,通过引入适合的电气元件,优化锂离子电池参数计算方法等途径,在更好提升锂离子电池等效电路模型建模精度的同时,也使其不至于过分复杂,从而更好地模拟锂电池真实工况. ...
1
... 这样改进的等效电路模型更接近锂离子电池真实工作情况,一定程度上提高了仿真精度,但是其对于电动势的修正值是不变的,并未考虑实际工况下迟滞电压值随SOC变化这一特性,所以精确度一般;文献[26 ]通过研究不同SOC对应的不同迟滞电压,将SOC分成5%~40%、40%~80%、80%~95%三个区间,并对应不同的迟滞电压值对模型进行修正,降低了模型的积累误差,对模型精度有较好的提升,但是没有考虑温度的影响;文献[27 ]将电池工作区间分为低SOC工作区间(SOC<20%)和高SOC工作区间(20%≤SOC≤100%),通过实验发现在低SOC工作区间时,温度对于SOC-OCV曲线的影响较大.且相较于高温环境,在低温环境下,不考虑迟滞效应将带来更大误差.文献[28 ]发现相同SOC时,最大滞回电压随着温度的升高而减小,从而建立了考虑温度影响的电池模型,通过模型验证使得其端电压输出误差减小50%,精度提高一倍;文献[29 ]建立了一个考虑容量衰减、自身温升、电池贮存等多因素影响的复杂锂电池模型,通过仿真验证了模型的精度.目前关于锂离子电池等效电路模型的研究主要是对其进行适当的改进,通过引入适合的电气元件,优化锂离子电池参数计算方法等途径,在更好提升锂离子电池等效电路模型建模精度的同时,也使其不至于过分复杂,从而更好地模拟锂电池真实工况. ...
1
... 这样改进的等效电路模型更接近锂离子电池真实工作情况,一定程度上提高了仿真精度,但是其对于电动势的修正值是不变的,并未考虑实际工况下迟滞电压值随SOC变化这一特性,所以精确度一般;文献[26 ]通过研究不同SOC对应的不同迟滞电压,将SOC分成5%~40%、40%~80%、80%~95%三个区间,并对应不同的迟滞电压值对模型进行修正,降低了模型的积累误差,对模型精度有较好的提升,但是没有考虑温度的影响;文献[27 ]将电池工作区间分为低SOC工作区间(SOC<20%)和高SOC工作区间(20%≤SOC≤100%),通过实验发现在低SOC工作区间时,温度对于SOC-OCV曲线的影响较大.且相较于高温环境,在低温环境下,不考虑迟滞效应将带来更大误差.文献[28 ]发现相同SOC时,最大滞回电压随着温度的升高而减小,从而建立了考虑温度影响的电池模型,通过模型验证使得其端电压输出误差减小50%,精度提高一倍;文献[29 ]建立了一个考虑容量衰减、自身温升、电池贮存等多因素影响的复杂锂电池模型,通过仿真验证了模型的精度.目前关于锂离子电池等效电路模型的研究主要是对其进行适当的改进,通过引入适合的电气元件,优化锂离子电池参数计算方法等途径,在更好提升锂离子电池等效电路模型建模精度的同时,也使其不至于过分复杂,从而更好地模拟锂电池真实工况. ...
1
... 这样改进的等效电路模型更接近锂离子电池真实工作情况,一定程度上提高了仿真精度,但是其对于电动势的修正值是不变的,并未考虑实际工况下迟滞电压值随SOC变化这一特性,所以精确度一般;文献[26 ]通过研究不同SOC对应的不同迟滞电压,将SOC分成5%~40%、40%~80%、80%~95%三个区间,并对应不同的迟滞电压值对模型进行修正,降低了模型的积累误差,对模型精度有较好的提升,但是没有考虑温度的影响;文献[27 ]将电池工作区间分为低SOC工作区间(SOC<20%)和高SOC工作区间(20%≤SOC≤100%),通过实验发现在低SOC工作区间时,温度对于SOC-OCV曲线的影响较大.且相较于高温环境,在低温环境下,不考虑迟滞效应将带来更大误差.文献[28 ]发现相同SOC时,最大滞回电压随着温度的升高而减小,从而建立了考虑温度影响的电池模型,通过模型验证使得其端电压输出误差减小50%,精度提高一倍;文献[29 ]建立了一个考虑容量衰减、自身温升、电池贮存等多因素影响的复杂锂电池模型,通过仿真验证了模型的精度.目前关于锂离子电池等效电路模型的研究主要是对其进行适当的改进,通过引入适合的电气元件,优化锂离子电池参数计算方法等途径,在更好提升锂离子电池等效电路模型建模精度的同时,也使其不至于过分复杂,从而更好地模拟锂电池真实工况. ...
1
... 这样改进的等效电路模型更接近锂离子电池真实工作情况,一定程度上提高了仿真精度,但是其对于电动势的修正值是不变的,并未考虑实际工况下迟滞电压值随SOC变化这一特性,所以精确度一般;文献[26 ]通过研究不同SOC对应的不同迟滞电压,将SOC分成5%~40%、40%~80%、80%~95%三个区间,并对应不同的迟滞电压值对模型进行修正,降低了模型的积累误差,对模型精度有较好的提升,但是没有考虑温度的影响;文献[27 ]将电池工作区间分为低SOC工作区间(SOC<20%)和高SOC工作区间(20%≤SOC≤100%),通过实验发现在低SOC工作区间时,温度对于SOC-OCV曲线的影响较大.且相较于高温环境,在低温环境下,不考虑迟滞效应将带来更大误差.文献[28 ]发现相同SOC时,最大滞回电压随着温度的升高而减小,从而建立了考虑温度影响的电池模型,通过模型验证使得其端电压输出误差减小50%,精度提高一倍;文献[29 ]建立了一个考虑容量衰减、自身温升、电池贮存等多因素影响的复杂锂电池模型,通过仿真验证了模型的精度.目前关于锂离子电池等效电路模型的研究主要是对其进行适当的改进,通过引入适合的电气元件,优化锂离子电池参数计算方法等途径,在更好提升锂离子电池等效电路模型建模精度的同时,也使其不至于过分复杂,从而更好地模拟锂电池真实工况. ...
1
... 为了实现储能系统的规模化,需要对电池单体串并联以提高其电流、电压和输出功率[30 ] .常用的电池成组方式有先并后串和先串后并[31 ] . ...
1
... 为了实现储能系统的规模化,需要对电池单体串并联以提高其电流、电压和输出功率[30 ] .常用的电池成组方式有先并后串和先串后并[31 ] . ...
1
... 为了实现储能系统的规模化,需要对电池单体串并联以提高其电流、电压和输出功率[30 ] .常用的电池成组方式有先并后串和先串后并[31 ] . ...
1
...
U 11 + U 12 + … + U 1 M = U 21 + U 22 + … + U 2 M = … = U N 1 + U N 2 + … + U N M 若某组串联出现问题,仅仅减小容量而不会使整个系统停止运行 容易出现电压过高[32 ] 由于电池制造材料和工艺的差别,要成组的电池单体之间的容量、内阻等描述电池特性的参数不尽相同.即使选择了性能相近的单体电池成组,随着电池组充放电次数的增加,也会因为老化而产生不一致性,且不一致性越大,电池组实际工作容量、功率、循环寿命就会越低[33 -34 ] ,若不考虑单体电池差异进行直接建模将会产生较大误差,所以建模过程中对电池差异性的分析十分必要.文献[35 ]通过研究不同电流对相同电池的影响,相同电流对不同电池的影响,相同电流、相同电池对不同SOC的影响,提出了“不一致性系数”来描述电池单体间的差异.文献[36 ]将不同内阻的单体电池并联,发现其充电电流大小不一致.将不同SOC的电池单体并联,发现单体间存在不平衡环流,且充电电流存在差异.对不同容量的电池单体并联并对其充电,发现了单体间相互平衡的自均流现象;这些现象会导致成组后电池性能的降低.文献[37 ]综合分析了并联电池单体间容量、内阻、SOC差异会产生不平衡电流,使电池受损,从而影响电池组的性能;文献[38 ]使用容量不同的电池单体串联,当最小容量的单体全部放电后电池串即退出运行,并用最小SOC的电池单体描述方程来组成表示电池串SOC值的模型,建立了考虑不一致性的电池组模型,和不考虑单体电池差异的模型同时应用于平抑风电波动的算例显示,考虑不一致性的模型精度更高,证明了考虑不一致性是电池建模的重要因素.所以在建模时应当引入时变参数和集总参数用来描述老化导致的不一致性对电池组性能的影响,从而实现建模精度的提升. ...
1
...
U 11 + U 12 + … + U 1 M = U 21 + U 22 + … + U 2 M = … = U N 1 + U N 2 + … + U N M 若某组串联出现问题,仅仅减小容量而不会使整个系统停止运行 容易出现电压过高[32 ] 由于电池制造材料和工艺的差别,要成组的电池单体之间的容量、内阻等描述电池特性的参数不尽相同.即使选择了性能相近的单体电池成组,随着电池组充放电次数的增加,也会因为老化而产生不一致性,且不一致性越大,电池组实际工作容量、功率、循环寿命就会越低[33 -34 ] ,若不考虑单体电池差异进行直接建模将会产生较大误差,所以建模过程中对电池差异性的分析十分必要.文献[35 ]通过研究不同电流对相同电池的影响,相同电流对不同电池的影响,相同电流、相同电池对不同SOC的影响,提出了“不一致性系数”来描述电池单体间的差异.文献[36 ]将不同内阻的单体电池并联,发现其充电电流大小不一致.将不同SOC的电池单体并联,发现单体间存在不平衡环流,且充电电流存在差异.对不同容量的电池单体并联并对其充电,发现了单体间相互平衡的自均流现象;这些现象会导致成组后电池性能的降低.文献[37 ]综合分析了并联电池单体间容量、内阻、SOC差异会产生不平衡电流,使电池受损,从而影响电池组的性能;文献[38 ]使用容量不同的电池单体串联,当最小容量的单体全部放电后电池串即退出运行,并用最小SOC的电池单体描述方程来组成表示电池串SOC值的模型,建立了考虑不一致性的电池组模型,和不考虑单体电池差异的模型同时应用于平抑风电波动的算例显示,考虑不一致性的模型精度更高,证明了考虑不一致性是电池建模的重要因素.所以在建模时应当引入时变参数和集总参数用来描述老化导致的不一致性对电池组性能的影响,从而实现建模精度的提升. ...
1
... 由于电池制造材料和工艺的差别,要成组的电池单体之间的容量、内阻等描述电池特性的参数不尽相同.即使选择了性能相近的单体电池成组,随着电池组充放电次数的增加,也会因为老化而产生不一致性,且不一致性越大,电池组实际工作容量、功率、循环寿命就会越低[33 -34 ] ,若不考虑单体电池差异进行直接建模将会产生较大误差,所以建模过程中对电池差异性的分析十分必要.文献[35 ]通过研究不同电流对相同电池的影响,相同电流对不同电池的影响,相同电流、相同电池对不同SOC的影响,提出了“不一致性系数”来描述电池单体间的差异.文献[36 ]将不同内阻的单体电池并联,发现其充电电流大小不一致.将不同SOC的电池单体并联,发现单体间存在不平衡环流,且充电电流存在差异.对不同容量的电池单体并联并对其充电,发现了单体间相互平衡的自均流现象;这些现象会导致成组后电池性能的降低.文献[37 ]综合分析了并联电池单体间容量、内阻、SOC差异会产生不平衡电流,使电池受损,从而影响电池组的性能;文献[38 ]使用容量不同的电池单体串联,当最小容量的单体全部放电后电池串即退出运行,并用最小SOC的电池单体描述方程来组成表示电池串SOC值的模型,建立了考虑不一致性的电池组模型,和不考虑单体电池差异的模型同时应用于平抑风电波动的算例显示,考虑不一致性的模型精度更高,证明了考虑不一致性是电池建模的重要因素.所以在建模时应当引入时变参数和集总参数用来描述老化导致的不一致性对电池组性能的影响,从而实现建模精度的提升. ...
1
... 由于电池制造材料和工艺的差别,要成组的电池单体之间的容量、内阻等描述电池特性的参数不尽相同.即使选择了性能相近的单体电池成组,随着电池组充放电次数的增加,也会因为老化而产生不一致性,且不一致性越大,电池组实际工作容量、功率、循环寿命就会越低[33 -34 ] ,若不考虑单体电池差异进行直接建模将会产生较大误差,所以建模过程中对电池差异性的分析十分必要.文献[35 ]通过研究不同电流对相同电池的影响,相同电流对不同电池的影响,相同电流、相同电池对不同SOC的影响,提出了“不一致性系数”来描述电池单体间的差异.文献[36 ]将不同内阻的单体电池并联,发现其充电电流大小不一致.将不同SOC的电池单体并联,发现单体间存在不平衡环流,且充电电流存在差异.对不同容量的电池单体并联并对其充电,发现了单体间相互平衡的自均流现象;这些现象会导致成组后电池性能的降低.文献[37 ]综合分析了并联电池单体间容量、内阻、SOC差异会产生不平衡电流,使电池受损,从而影响电池组的性能;文献[38 ]使用容量不同的电池单体串联,当最小容量的单体全部放电后电池串即退出运行,并用最小SOC的电池单体描述方程来组成表示电池串SOC值的模型,建立了考虑不一致性的电池组模型,和不考虑单体电池差异的模型同时应用于平抑风电波动的算例显示,考虑不一致性的模型精度更高,证明了考虑不一致性是电池建模的重要因素.所以在建模时应当引入时变参数和集总参数用来描述老化导致的不一致性对电池组性能的影响,从而实现建模精度的提升. ...
1
... 由于电池制造材料和工艺的差别,要成组的电池单体之间的容量、内阻等描述电池特性的参数不尽相同.即使选择了性能相近的单体电池成组,随着电池组充放电次数的增加,也会因为老化而产生不一致性,且不一致性越大,电池组实际工作容量、功率、循环寿命就会越低[33 -34 ] ,若不考虑单体电池差异进行直接建模将会产生较大误差,所以建模过程中对电池差异性的分析十分必要.文献[35 ]通过研究不同电流对相同电池的影响,相同电流对不同电池的影响,相同电流、相同电池对不同SOC的影响,提出了“不一致性系数”来描述电池单体间的差异.文献[36 ]将不同内阻的单体电池并联,发现其充电电流大小不一致.将不同SOC的电池单体并联,发现单体间存在不平衡环流,且充电电流存在差异.对不同容量的电池单体并联并对其充电,发现了单体间相互平衡的自均流现象;这些现象会导致成组后电池性能的降低.文献[37 ]综合分析了并联电池单体间容量、内阻、SOC差异会产生不平衡电流,使电池受损,从而影响电池组的性能;文献[38 ]使用容量不同的电池单体串联,当最小容量的单体全部放电后电池串即退出运行,并用最小SOC的电池单体描述方程来组成表示电池串SOC值的模型,建立了考虑不一致性的电池组模型,和不考虑单体电池差异的模型同时应用于平抑风电波动的算例显示,考虑不一致性的模型精度更高,证明了考虑不一致性是电池建模的重要因素.所以在建模时应当引入时变参数和集总参数用来描述老化导致的不一致性对电池组性能的影响,从而实现建模精度的提升. ...
1
... 由于电池制造材料和工艺的差别,要成组的电池单体之间的容量、内阻等描述电池特性的参数不尽相同.即使选择了性能相近的单体电池成组,随着电池组充放电次数的增加,也会因为老化而产生不一致性,且不一致性越大,电池组实际工作容量、功率、循环寿命就会越低[33 -34 ] ,若不考虑单体电池差异进行直接建模将会产生较大误差,所以建模过程中对电池差异性的分析十分必要.文献[35 ]通过研究不同电流对相同电池的影响,相同电流对不同电池的影响,相同电流、相同电池对不同SOC的影响,提出了“不一致性系数”来描述电池单体间的差异.文献[36 ]将不同内阻的单体电池并联,发现其充电电流大小不一致.将不同SOC的电池单体并联,发现单体间存在不平衡环流,且充电电流存在差异.对不同容量的电池单体并联并对其充电,发现了单体间相互平衡的自均流现象;这些现象会导致成组后电池性能的降低.文献[37 ]综合分析了并联电池单体间容量、内阻、SOC差异会产生不平衡电流,使电池受损,从而影响电池组的性能;文献[38 ]使用容量不同的电池单体串联,当最小容量的单体全部放电后电池串即退出运行,并用最小SOC的电池单体描述方程来组成表示电池串SOC值的模型,建立了考虑不一致性的电池组模型,和不考虑单体电池差异的模型同时应用于平抑风电波动的算例显示,考虑不一致性的模型精度更高,证明了考虑不一致性是电池建模的重要因素.所以在建模时应当引入时变参数和集总参数用来描述老化导致的不一致性对电池组性能的影响,从而实现建模精度的提升. ...
1
... 由于电池制造材料和工艺的差别,要成组的电池单体之间的容量、内阻等描述电池特性的参数不尽相同.即使选择了性能相近的单体电池成组,随着电池组充放电次数的增加,也会因为老化而产生不一致性,且不一致性越大,电池组实际工作容量、功率、循环寿命就会越低[33 -34 ] ,若不考虑单体电池差异进行直接建模将会产生较大误差,所以建模过程中对电池差异性的分析十分必要.文献[35 ]通过研究不同电流对相同电池的影响,相同电流对不同电池的影响,相同电流、相同电池对不同SOC的影响,提出了“不一致性系数”来描述电池单体间的差异.文献[36 ]将不同内阻的单体电池并联,发现其充电电流大小不一致.将不同SOC的电池单体并联,发现单体间存在不平衡环流,且充电电流存在差异.对不同容量的电池单体并联并对其充电,发现了单体间相互平衡的自均流现象;这些现象会导致成组后电池性能的降低.文献[37 ]综合分析了并联电池单体间容量、内阻、SOC差异会产生不平衡电流,使电池受损,从而影响电池组的性能;文献[38 ]使用容量不同的电池单体串联,当最小容量的单体全部放电后电池串即退出运行,并用最小SOC的电池单体描述方程来组成表示电池串SOC值的模型,建立了考虑不一致性的电池组模型,和不考虑单体电池差异的模型同时应用于平抑风电波动的算例显示,考虑不一致性的模型精度更高,证明了考虑不一致性是电池建模的重要因素.所以在建模时应当引入时变参数和集总参数用来描述老化导致的不一致性对电池组性能的影响,从而实现建模精度的提升. ...
1
... 由于电池制造材料和工艺的差别,要成组的电池单体之间的容量、内阻等描述电池特性的参数不尽相同.即使选择了性能相近的单体电池成组,随着电池组充放电次数的增加,也会因为老化而产生不一致性,且不一致性越大,电池组实际工作容量、功率、循环寿命就会越低[33 -34 ] ,若不考虑单体电池差异进行直接建模将会产生较大误差,所以建模过程中对电池差异性的分析十分必要.文献[35 ]通过研究不同电流对相同电池的影响,相同电流对不同电池的影响,相同电流、相同电池对不同SOC的影响,提出了“不一致性系数”来描述电池单体间的差异.文献[36 ]将不同内阻的单体电池并联,发现其充电电流大小不一致.将不同SOC的电池单体并联,发现单体间存在不平衡环流,且充电电流存在差异.对不同容量的电池单体并联并对其充电,发现了单体间相互平衡的自均流现象;这些现象会导致成组后电池性能的降低.文献[37 ]综合分析了并联电池单体间容量、内阻、SOC差异会产生不平衡电流,使电池受损,从而影响电池组的性能;文献[38 ]使用容量不同的电池单体串联,当最小容量的单体全部放电后电池串即退出运行,并用最小SOC的电池单体描述方程来组成表示电池串SOC值的模型,建立了考虑不一致性的电池组模型,和不考虑单体电池差异的模型同时应用于平抑风电波动的算例显示,考虑不一致性的模型精度更高,证明了考虑不一致性是电池建模的重要因素.所以在建模时应当引入时变参数和集总参数用来描述老化导致的不一致性对电池组性能的影响,从而实现建模精度的提升. ...
1
... 由于电池制造材料和工艺的差别,要成组的电池单体之间的容量、内阻等描述电池特性的参数不尽相同.即使选择了性能相近的单体电池成组,随着电池组充放电次数的增加,也会因为老化而产生不一致性,且不一致性越大,电池组实际工作容量、功率、循环寿命就会越低[33 -34 ] ,若不考虑单体电池差异进行直接建模将会产生较大误差,所以建模过程中对电池差异性的分析十分必要.文献[35 ]通过研究不同电流对相同电池的影响,相同电流对不同电池的影响,相同电流、相同电池对不同SOC的影响,提出了“不一致性系数”来描述电池单体间的差异.文献[36 ]将不同内阻的单体电池并联,发现其充电电流大小不一致.将不同SOC的电池单体并联,发现单体间存在不平衡环流,且充电电流存在差异.对不同容量的电池单体并联并对其充电,发现了单体间相互平衡的自均流现象;这些现象会导致成组后电池性能的降低.文献[37 ]综合分析了并联电池单体间容量、内阻、SOC差异会产生不平衡电流,使电池受损,从而影响电池组的性能;文献[38 ]使用容量不同的电池单体串联,当最小容量的单体全部放电后电池串即退出运行,并用最小SOC的电池单体描述方程来组成表示电池串SOC值的模型,建立了考虑不一致性的电池组模型,和不考虑单体电池差异的模型同时应用于平抑风电波动的算例显示,考虑不一致性的模型精度更高,证明了考虑不一致性是电池建模的重要因素.所以在建模时应当引入时变参数和集总参数用来描述老化导致的不一致性对电池组性能的影响,从而实现建模精度的提升. ...
1
... 由于电池制造材料和工艺的差别,要成组的电池单体之间的容量、内阻等描述电池特性的参数不尽相同.即使选择了性能相近的单体电池成组,随着电池组充放电次数的增加,也会因为老化而产生不一致性,且不一致性越大,电池组实际工作容量、功率、循环寿命就会越低[33 -34 ] ,若不考虑单体电池差异进行直接建模将会产生较大误差,所以建模过程中对电池差异性的分析十分必要.文献[35 ]通过研究不同电流对相同电池的影响,相同电流对不同电池的影响,相同电流、相同电池对不同SOC的影响,提出了“不一致性系数”来描述电池单体间的差异.文献[36 ]将不同内阻的单体电池并联,发现其充电电流大小不一致.将不同SOC的电池单体并联,发现单体间存在不平衡环流,且充电电流存在差异.对不同容量的电池单体并联并对其充电,发现了单体间相互平衡的自均流现象;这些现象会导致成组后电池性能的降低.文献[37 ]综合分析了并联电池单体间容量、内阻、SOC差异会产生不平衡电流,使电池受损,从而影响电池组的性能;文献[38 ]使用容量不同的电池单体串联,当最小容量的单体全部放电后电池串即退出运行,并用最小SOC的电池单体描述方程来组成表示电池串SOC值的模型,建立了考虑不一致性的电池组模型,和不考虑单体电池差异的模型同时应用于平抑风电波动的算例显示,考虑不一致性的模型精度更高,证明了考虑不一致性是电池建模的重要因素.所以在建模时应当引入时变参数和集总参数用来描述老化导致的不一致性对电池组性能的影响,从而实现建模精度的提升. ...
1
... 由于电池制造材料和工艺的差别,要成组的电池单体之间的容量、内阻等描述电池特性的参数不尽相同.即使选择了性能相近的单体电池成组,随着电池组充放电次数的增加,也会因为老化而产生不一致性,且不一致性越大,电池组实际工作容量、功率、循环寿命就会越低[33 -34 ] ,若不考虑单体电池差异进行直接建模将会产生较大误差,所以建模过程中对电池差异性的分析十分必要.文献[35 ]通过研究不同电流对相同电池的影响,相同电流对不同电池的影响,相同电流、相同电池对不同SOC的影响,提出了“不一致性系数”来描述电池单体间的差异.文献[36 ]将不同内阻的单体电池并联,发现其充电电流大小不一致.将不同SOC的电池单体并联,发现单体间存在不平衡环流,且充电电流存在差异.对不同容量的电池单体并联并对其充电,发现了单体间相互平衡的自均流现象;这些现象会导致成组后电池性能的降低.文献[37 ]综合分析了并联电池单体间容量、内阻、SOC差异会产生不平衡电流,使电池受损,从而影响电池组的性能;文献[38 ]使用容量不同的电池单体串联,当最小容量的单体全部放电后电池串即退出运行,并用最小SOC的电池单体描述方程来组成表示电池串SOC值的模型,建立了考虑不一致性的电池组模型,和不考虑单体电池差异的模型同时应用于平抑风电波动的算例显示,考虑不一致性的模型精度更高,证明了考虑不一致性是电池建模的重要因素.所以在建模时应当引入时变参数和集总参数用来描述老化导致的不一致性对电池组性能的影响,从而实现建模精度的提升. ...
1
... 由于电池制造材料和工艺的差别,要成组的电池单体之间的容量、内阻等描述电池特性的参数不尽相同.即使选择了性能相近的单体电池成组,随着电池组充放电次数的增加,也会因为老化而产生不一致性,且不一致性越大,电池组实际工作容量、功率、循环寿命就会越低[33 -34 ] ,若不考虑单体电池差异进行直接建模将会产生较大误差,所以建模过程中对电池差异性的分析十分必要.文献[35 ]通过研究不同电流对相同电池的影响,相同电流对不同电池的影响,相同电流、相同电池对不同SOC的影响,提出了“不一致性系数”来描述电池单体间的差异.文献[36 ]将不同内阻的单体电池并联,发现其充电电流大小不一致.将不同SOC的电池单体并联,发现单体间存在不平衡环流,且充电电流存在差异.对不同容量的电池单体并联并对其充电,发现了单体间相互平衡的自均流现象;这些现象会导致成组后电池性能的降低.文献[37 ]综合分析了并联电池单体间容量、内阻、SOC差异会产生不平衡电流,使电池受损,从而影响电池组的性能;文献[38 ]使用容量不同的电池单体串联,当最小容量的单体全部放电后电池串即退出运行,并用最小SOC的电池单体描述方程来组成表示电池串SOC值的模型,建立了考虑不一致性的电池组模型,和不考虑单体电池差异的模型同时应用于平抑风电波动的算例显示,考虑不一致性的模型精度更高,证明了考虑不一致性是电池建模的重要因素.所以在建模时应当引入时变参数和集总参数用来描述老化导致的不一致性对电池组性能的影响,从而实现建模精度的提升. ...
1
... 由于电池制造材料和工艺的差别,要成组的电池单体之间的容量、内阻等描述电池特性的参数不尽相同.即使选择了性能相近的单体电池成组,随着电池组充放电次数的增加,也会因为老化而产生不一致性,且不一致性越大,电池组实际工作容量、功率、循环寿命就会越低[33 -34 ] ,若不考虑单体电池差异进行直接建模将会产生较大误差,所以建模过程中对电池差异性的分析十分必要.文献[35 ]通过研究不同电流对相同电池的影响,相同电流对不同电池的影响,相同电流、相同电池对不同SOC的影响,提出了“不一致性系数”来描述电池单体间的差异.文献[36 ]将不同内阻的单体电池并联,发现其充电电流大小不一致.将不同SOC的电池单体并联,发现单体间存在不平衡环流,且充电电流存在差异.对不同容量的电池单体并联并对其充电,发现了单体间相互平衡的自均流现象;这些现象会导致成组后电池性能的降低.文献[37 ]综合分析了并联电池单体间容量、内阻、SOC差异会产生不平衡电流,使电池受损,从而影响电池组的性能;文献[38 ]使用容量不同的电池单体串联,当最小容量的单体全部放电后电池串即退出运行,并用最小SOC的电池单体描述方程来组成表示电池串SOC值的模型,建立了考虑不一致性的电池组模型,和不考虑单体电池差异的模型同时应用于平抑风电波动的算例显示,考虑不一致性的模型精度更高,证明了考虑不一致性是电池建模的重要因素.所以在建模时应当引入时变参数和集总参数用来描述老化导致的不一致性对电池组性能的影响,从而实现建模精度的提升. ...
1
... 由于电池制造材料和工艺的差别,要成组的电池单体之间的容量、内阻等描述电池特性的参数不尽相同.即使选择了性能相近的单体电池成组,随着电池组充放电次数的增加,也会因为老化而产生不一致性,且不一致性越大,电池组实际工作容量、功率、循环寿命就会越低[33 -34 ] ,若不考虑单体电池差异进行直接建模将会产生较大误差,所以建模过程中对电池差异性的分析十分必要.文献[35 ]通过研究不同电流对相同电池的影响,相同电流对不同电池的影响,相同电流、相同电池对不同SOC的影响,提出了“不一致性系数”来描述电池单体间的差异.文献[36 ]将不同内阻的单体电池并联,发现其充电电流大小不一致.将不同SOC的电池单体并联,发现单体间存在不平衡环流,且充电电流存在差异.对不同容量的电池单体并联并对其充电,发现了单体间相互平衡的自均流现象;这些现象会导致成组后电池性能的降低.文献[37 ]综合分析了并联电池单体间容量、内阻、SOC差异会产生不平衡电流,使电池受损,从而影响电池组的性能;文献[38 ]使用容量不同的电池单体串联,当最小容量的单体全部放电后电池串即退出运行,并用最小SOC的电池单体描述方程来组成表示电池串SOC值的模型,建立了考虑不一致性的电池组模型,和不考虑单体电池差异的模型同时应用于平抑风电波动的算例显示,考虑不一致性的模型精度更高,证明了考虑不一致性是电池建模的重要因素.所以在建模时应当引入时变参数和集总参数用来描述老化导致的不一致性对电池组性能的影响,从而实现建模精度的提升. ...
1
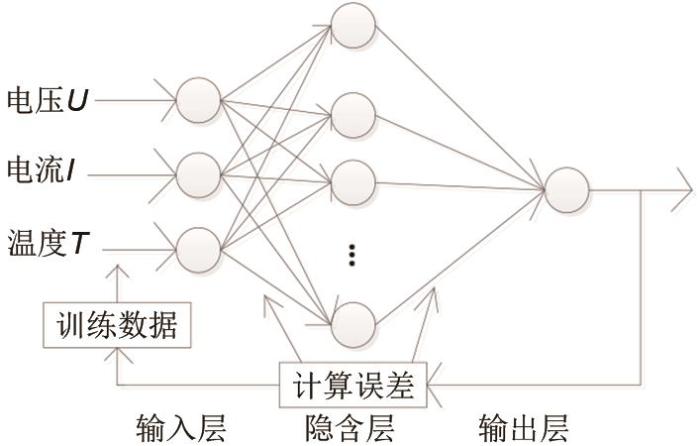
... 神经网络是基于生物神经元之间传递信息方式建立起来的一种方法,它可以分布储存信息和并行处理信息,具有高效性.结合其非线性的特点,相较于决策树、K近邻、支持向量机等锂电池建模方法,神经网络比较适用于锂电池的建模研究[39 -40 ] .比较常用的是BP神经网络模型,其包括输入层、隐含层、输出层三层网络结构[41 ] ,它将电压、电流、温度参数作为输入,将电池的SOC作为输出,且不断反馈,以获得适当的连接权值和偏差,在可以达到一定精度的同时,也具有一定的速度优势[42 ] . ...
1
... 神经网络是基于生物神经元之间传递信息方式建立起来的一种方法,它可以分布储存信息和并行处理信息,具有高效性.结合其非线性的特点,相较于决策树、K近邻、支持向量机等锂电池建模方法,神经网络比较适用于锂电池的建模研究[39 -40 ] .比较常用的是BP神经网络模型,其包括输入层、隐含层、输出层三层网络结构[41 ] ,它将电压、电流、温度参数作为输入,将电池的SOC作为输出,且不断反馈,以获得适当的连接权值和偏差,在可以达到一定精度的同时,也具有一定的速度优势[42 ] . ...
1
... 神经网络是基于生物神经元之间传递信息方式建立起来的一种方法,它可以分布储存信息和并行处理信息,具有高效性.结合其非线性的特点,相较于决策树、K近邻、支持向量机等锂电池建模方法,神经网络比较适用于锂电池的建模研究[39 -40 ] .比较常用的是BP神经网络模型,其包括输入层、隐含层、输出层三层网络结构[41 ] ,它将电压、电流、温度参数作为输入,将电池的SOC作为输出,且不断反馈,以获得适当的连接权值和偏差,在可以达到一定精度的同时,也具有一定的速度优势[42 ] . ...
1
... 神经网络是基于生物神经元之间传递信息方式建立起来的一种方法,它可以分布储存信息和并行处理信息,具有高效性.结合其非线性的特点,相较于决策树、K近邻、支持向量机等锂电池建模方法,神经网络比较适用于锂电池的建模研究[39 -40 ] .比较常用的是BP神经网络模型,其包括输入层、隐含层、输出层三层网络结构[41 ] ,它将电压、电流、温度参数作为输入,将电池的SOC作为输出,且不断反馈,以获得适当的连接权值和偏差,在可以达到一定精度的同时,也具有一定的速度优势[42 ] . ...
2
... 神经网络是基于生物神经元之间传递信息方式建立起来的一种方法,它可以分布储存信息和并行处理信息,具有高效性.结合其非线性的特点,相较于决策树、K近邻、支持向量机等锂电池建模方法,神经网络比较适用于锂电池的建模研究[39 -40 ] .比较常用的是BP神经网络模型,其包括输入层、隐含层、输出层三层网络结构[41 ] ,它将电压、电流、温度参数作为输入,将电池的SOC作为输出,且不断反馈,以获得适当的连接权值和偏差,在可以达到一定精度的同时,也具有一定的速度优势[42 ] . ...
... 神经网络模型不注重对电池机理的研究,是通过训练获得输入与输出的关系,所以输出精度取决于训练的数量和质量[43 ] .所以对于训练不足或数据不满足要求时,训练效率较低,误差较大.学者们对神经网络法从不同方面进行了不同的改进,从而提高了训练效率和模型精度.如文献[42 ]提出改进传递函数的方法,将隐含层和输出层函数分别设置为非线性和线性来提高网络的训练速度和精度,但是这种方法只对函数进行了优化,却没有优化参数;文献[44 ]针对模型参数问题,分析了神经网络权值和阈值随机初始化的问题,认为其造成局部极值影响了模型的精度;同时研究了免疫遗传算法IGA,利用其多样性和可维持极值的特点,让模型能够使用优化后的参数进行初始化,避免局部极值,从而达到提高模型精度的目的.利用免疫遗传算法具有记忆性的特点,还可减少训练次数,提高了网络的训练效率;文献[45 ]利用元胞自动机可以通过邻居的状态来预测自己在下一时刻状态的特点,在元胞体内存放需要训练的网络,通过网络内部的互相学习,提高了模型精度;综上所述,目前对于神经网络模型的研究主要针对网络自身结构,或结合其他模型特点对神经网络建模法进行优化,使建模精度和训练效率得到有效提高. ...
2
... 神经网络是基于生物神经元之间传递信息方式建立起来的一种方法,它可以分布储存信息和并行处理信息,具有高效性.结合其非线性的特点,相较于决策树、K近邻、支持向量机等锂电池建模方法,神经网络比较适用于锂电池的建模研究[39 -40 ] .比较常用的是BP神经网络模型,其包括输入层、隐含层、输出层三层网络结构[41 ] ,它将电压、电流、温度参数作为输入,将电池的SOC作为输出,且不断反馈,以获得适当的连接权值和偏差,在可以达到一定精度的同时,也具有一定的速度优势[42 ] . ...
... 神经网络模型不注重对电池机理的研究,是通过训练获得输入与输出的关系,所以输出精度取决于训练的数量和质量[43 ] .所以对于训练不足或数据不满足要求时,训练效率较低,误差较大.学者们对神经网络法从不同方面进行了不同的改进,从而提高了训练效率和模型精度.如文献[42 ]提出改进传递函数的方法,将隐含层和输出层函数分别设置为非线性和线性来提高网络的训练速度和精度,但是这种方法只对函数进行了优化,却没有优化参数;文献[44 ]针对模型参数问题,分析了神经网络权值和阈值随机初始化的问题,认为其造成局部极值影响了模型的精度;同时研究了免疫遗传算法IGA,利用其多样性和可维持极值的特点,让模型能够使用优化后的参数进行初始化,避免局部极值,从而达到提高模型精度的目的.利用免疫遗传算法具有记忆性的特点,还可减少训练次数,提高了网络的训练效率;文献[45 ]利用元胞自动机可以通过邻居的状态来预测自己在下一时刻状态的特点,在元胞体内存放需要训练的网络,通过网络内部的互相学习,提高了模型精度;综上所述,目前对于神经网络模型的研究主要针对网络自身结构,或结合其他模型特点对神经网络建模法进行优化,使建模精度和训练效率得到有效提高. ...
1
... 神经网络模型不注重对电池机理的研究,是通过训练获得输入与输出的关系,所以输出精度取决于训练的数量和质量[43 ] .所以对于训练不足或数据不满足要求时,训练效率较低,误差较大.学者们对神经网络法从不同方面进行了不同的改进,从而提高了训练效率和模型精度.如文献[42 ]提出改进传递函数的方法,将隐含层和输出层函数分别设置为非线性和线性来提高网络的训练速度和精度,但是这种方法只对函数进行了优化,却没有优化参数;文献[44 ]针对模型参数问题,分析了神经网络权值和阈值随机初始化的问题,认为其造成局部极值影响了模型的精度;同时研究了免疫遗传算法IGA,利用其多样性和可维持极值的特点,让模型能够使用优化后的参数进行初始化,避免局部极值,从而达到提高模型精度的目的.利用免疫遗传算法具有记忆性的特点,还可减少训练次数,提高了网络的训练效率;文献[45 ]利用元胞自动机可以通过邻居的状态来预测自己在下一时刻状态的特点,在元胞体内存放需要训练的网络,通过网络内部的互相学习,提高了模型精度;综上所述,目前对于神经网络模型的研究主要针对网络自身结构,或结合其他模型特点对神经网络建模法进行优化,使建模精度和训练效率得到有效提高. ...
1
... 神经网络模型不注重对电池机理的研究,是通过训练获得输入与输出的关系,所以输出精度取决于训练的数量和质量[43 ] .所以对于训练不足或数据不满足要求时,训练效率较低,误差较大.学者们对神经网络法从不同方面进行了不同的改进,从而提高了训练效率和模型精度.如文献[42 ]提出改进传递函数的方法,将隐含层和输出层函数分别设置为非线性和线性来提高网络的训练速度和精度,但是这种方法只对函数进行了优化,却没有优化参数;文献[44 ]针对模型参数问题,分析了神经网络权值和阈值随机初始化的问题,认为其造成局部极值影响了模型的精度;同时研究了免疫遗传算法IGA,利用其多样性和可维持极值的特点,让模型能够使用优化后的参数进行初始化,避免局部极值,从而达到提高模型精度的目的.利用免疫遗传算法具有记忆性的特点,还可减少训练次数,提高了网络的训练效率;文献[45 ]利用元胞自动机可以通过邻居的状态来预测自己在下一时刻状态的特点,在元胞体内存放需要训练的网络,通过网络内部的互相学习,提高了模型精度;综上所述,目前对于神经网络模型的研究主要针对网络自身结构,或结合其他模型特点对神经网络建模法进行优化,使建模精度和训练效率得到有效提高. ...
1
... 神经网络模型不注重对电池机理的研究,是通过训练获得输入与输出的关系,所以输出精度取决于训练的数量和质量[43 ] .所以对于训练不足或数据不满足要求时,训练效率较低,误差较大.学者们对神经网络法从不同方面进行了不同的改进,从而提高了训练效率和模型精度.如文献[42 ]提出改进传递函数的方法,将隐含层和输出层函数分别设置为非线性和线性来提高网络的训练速度和精度,但是这种方法只对函数进行了优化,却没有优化参数;文献[44 ]针对模型参数问题,分析了神经网络权值和阈值随机初始化的问题,认为其造成局部极值影响了模型的精度;同时研究了免疫遗传算法IGA,利用其多样性和可维持极值的特点,让模型能够使用优化后的参数进行初始化,避免局部极值,从而达到提高模型精度的目的.利用免疫遗传算法具有记忆性的特点,还可减少训练次数,提高了网络的训练效率;文献[45 ]利用元胞自动机可以通过邻居的状态来预测自己在下一时刻状态的特点,在元胞体内存放需要训练的网络,通过网络内部的互相学习,提高了模型精度;综上所述,目前对于神经网络模型的研究主要针对网络自身结构,或结合其他模型特点对神经网络建模法进行优化,使建模精度和训练效率得到有效提高. ...
1
... 神经网络模型不注重对电池机理的研究,是通过训练获得输入与输出的关系,所以输出精度取决于训练的数量和质量[43 ] .所以对于训练不足或数据不满足要求时,训练效率较低,误差较大.学者们对神经网络法从不同方面进行了不同的改进,从而提高了训练效率和模型精度.如文献[42 ]提出改进传递函数的方法,将隐含层和输出层函数分别设置为非线性和线性来提高网络的训练速度和精度,但是这种方法只对函数进行了优化,却没有优化参数;文献[44 ]针对模型参数问题,分析了神经网络权值和阈值随机初始化的问题,认为其造成局部极值影响了模型的精度;同时研究了免疫遗传算法IGA,利用其多样性和可维持极值的特点,让模型能够使用优化后的参数进行初始化,避免局部极值,从而达到提高模型精度的目的.利用免疫遗传算法具有记忆性的特点,还可减少训练次数,提高了网络的训练效率;文献[45 ]利用元胞自动机可以通过邻居的状态来预测自己在下一时刻状态的特点,在元胞体内存放需要训练的网络,通过网络内部的互相学习,提高了模型精度;综上所述,目前对于神经网络模型的研究主要针对网络自身结构,或结合其他模型特点对神经网络建模法进行优化,使建模精度和训练效率得到有效提高. ...
1
... 神经网络模型不注重对电池机理的研究,是通过训练获得输入与输出的关系,所以输出精度取决于训练的数量和质量[43 ] .所以对于训练不足或数据不满足要求时,训练效率较低,误差较大.学者们对神经网络法从不同方面进行了不同的改进,从而提高了训练效率和模型精度.如文献[42 ]提出改进传递函数的方法,将隐含层和输出层函数分别设置为非线性和线性来提高网络的训练速度和精度,但是这种方法只对函数进行了优化,却没有优化参数;文献[44 ]针对模型参数问题,分析了神经网络权值和阈值随机初始化的问题,认为其造成局部极值影响了模型的精度;同时研究了免疫遗传算法IGA,利用其多样性和可维持极值的特点,让模型能够使用优化后的参数进行初始化,避免局部极值,从而达到提高模型精度的目的.利用免疫遗传算法具有记忆性的特点,还可减少训练次数,提高了网络的训练效率;文献[45 ]利用元胞自动机可以通过邻居的状态来预测自己在下一时刻状态的特点,在元胞体内存放需要训练的网络,通过网络内部的互相学习,提高了模型精度;综上所述,目前对于神经网络模型的研究主要针对网络自身结构,或结合其他模型特点对神经网络建模法进行优化,使建模精度和训练效率得到有效提高. ...
1
... 神经网络模型不注重对电池机理的研究,是通过训练获得输入与输出的关系,所以输出精度取决于训练的数量和质量[43 ] .所以对于训练不足或数据不满足要求时,训练效率较低,误差较大.学者们对神经网络法从不同方面进行了不同的改进,从而提高了训练效率和模型精度.如文献[42 ]提出改进传递函数的方法,将隐含层和输出层函数分别设置为非线性和线性来提高网络的训练速度和精度,但是这种方法只对函数进行了优化,却没有优化参数;文献[44 ]针对模型参数问题,分析了神经网络权值和阈值随机初始化的问题,认为其造成局部极值影响了模型的精度;同时研究了免疫遗传算法IGA,利用其多样性和可维持极值的特点,让模型能够使用优化后的参数进行初始化,避免局部极值,从而达到提高模型精度的目的.利用免疫遗传算法具有记忆性的特点,还可减少训练次数,提高了网络的训练效率;文献[45 ]利用元胞自动机可以通过邻居的状态来预测自己在下一时刻状态的特点,在元胞体内存放需要训练的网络,通过网络内部的互相学习,提高了模型精度;综上所述,目前对于神经网络模型的研究主要针对网络自身结构,或结合其他模型特点对神经网络建模法进行优化,使建模精度和训练效率得到有效提高. ...