[1]
刘畅, 卓建坤, 赵东明, 等. 利用储能系统实现可再生能源微电网灵活安全运行的研究综述[J]. 中国电机工程学报, 2020, 40(1): 1-18, 369.
[本文引用: 1]
LIU C, ZHUO J K, ZHAO D M, et al. A review on the utilization of energy storage system for the flexible and safe operation of renewable energy microgrids[J]. Proceedings of the CSEE, 2020, 40(1): 1-18, 369.
[本文引用: 1]
[2]
王成山, 李微, 王议锋, 等. 直流微电网母线电压波动分类及抑制方法综述[J]. 中国电机工程学报, 2017, 37(1): 84-98.
[本文引用: 1]
WANG Chengshan, LI Wei, WANG Yifeng, et al. DC bus voltage fluctuation classification and restraint methods review for DC microgrid[J]. Proceedings of The Chinese Society for Electrical Engineering, 2017, 37(1): 84-98.
[本文引用: 1]
[3]
蒋智化, 刘连光, 刘自发, 等. 直流配电网功率控制策略与电压波动研究[J]. 中国电机工程学报, 2016, 36(4): 919-926.
[本文引用: 1]
JIANG Zhihua, LIU Lianguang, LIU Zifa, et al. Research on power flow control and the voltage fluctuation characteristics of DC distribution networks based on different control strategies[J]. Proceedings of The Chinese Society for Electrical Engineering, 2016, 36(4): 919-926.
[本文引用: 1]
[4]
房建军. 储能在光伏低压直流供电建筑中的作用和应用[J]. 储能科学与技术, 2021, 10(2): 624-629.
[本文引用: 1]
FANG J J. Function and practice of photovoltaic building energy storage system with low-voltage DC power supply[J]. Energy Storage Science and Technology, 2021, 10(2): 624-629.
[本文引用: 1]
[5]
马钊,赵志刚,孙媛媛,等.新一代低压直流供用电系统关键技术及发展展望[J].电力系统自动化,2019,43(23):12-22.MA Z, ZHAO Z G, SUN Y Y, et al. Key technologies and development prospect of new generation low-voltage DC power supply and utilization system[J]. Automation of Electric Power Systems, 2019, 43(23): 12-22.
[本文引用: 1]
[6]
夏杨红, 韦巍.电力电子化电力系统暂态稳定分析新框架:基于耦合因子的非线性解耦方法[J]. 中国电机工程学报, 2020, 40(16): 5102-5113.
[本文引用: 1]
XIA Y H, WEI W. New analysis framework for transient stability evaluation of power electronics dominated power system: coupling factors based nonlinear decoupling method[J]. Proceedings of The Chinese Society for Electrical Engineering, 2020, 40(16): 5102-5113.
[本文引用: 1]
[7]
章宝歌, 张振, 王东豪, 等. 一种适用于复合储能的双向DC/DC变换器[J]. 储能科学与技术, 2020, 9(1): 178-185.
[本文引用: 1]
ZHANG B G, ZHANG Z, WANG D H, et al. A bidirectional DC/DC converter for hybrid energy storage system[J]. Energy Storage Science and Technology, 2020, 9(1): 178-185.
[本文引用: 1]
[8]
刘志坚, 李晓磊, 梁宁, 等. 基于前馈自抗扰控制方法的蓄电池储能控制策略[J]. 电机与控制应用, 2020, 47(6): 97-102.
[本文引用: 1]
LIU Z J, LI X L, LIANG N, et al. Battery energy storage control strategy based on feedforward active disturbance rejection control method[J]. Electric Machines & Control Application, 2020, 47(6): 97-102.
[本文引用: 1]
[9]
GORJI S A, SAHEBI H G, EKTESABI M, et al. Topologies and control schemes of bidirectional DC-DC power converters: An overview[J]. IEEE Access, 2019, 7: 117997-118019.
[本文引用: 1]
[10]
SHAO X Y, HU J, ZHAO Z T. Stabilisation strategy based on feedback linearisation for DC microgrid with multi-converter[J]. The Journal of Engineering, 2019, 2019(16): 1802-1806.
[本文引用: 1]
[11]
MARTINEZ-TREVIÑO B A, EL AROUDI A, VIDAL-IDIARTE E, et al. Sliding-mode control of a boost converter under constant power loading conditions[J]. IET Power Electronics, 2019, 12(3): 521-529.
[本文引用: 1]
[12]
YE B J, LIU Y L, WU Z F. Research on sliding mode control strategy for bidirectional DC/DC energy storage converter[C]// 2019 IEEE International Conference on Electron Devices and Solid-State Circuits (EDSSC). June 12-14, 2019 , Xi'an, China. IEEE, 2019: 1-3.
[本文引用: 1]
[13]
李洪恩, 胡健, 唐志扬, 等. 孤岛直流微电网DC-DC变换器的非线性控制技术[J]. 电源学报, 2020, 18(2): 4-14.
[本文引用: 3]
LI H E, HU J, TANG Z Y, et al. Nonlinear control technology for DC-DC converter in islanded DC microgrid[J]. Journal of Power Supply, 2020, 18(2): 4-14.
[本文引用: 3]
[14]
ARMGHAN H, YANG M, WANG M Q, et al. Nonlinear integral backstepping based control of a DC microgrid with renewable generation and energy storage systems[J]. International Journal of Electrical Power & Energy Systems, 2020, 117: 105613.
[本文引用: 1]
[15]
王宝华, 蒋力. 基于精确反馈线性化的直流微电网双向直流变换器反步滑模控制[J]. 电力系统保护与控制, 2018, 46(2): 43-49.
[本文引用: 2]
WANG B H, JIANG L. Backstepping sliding mode control based on exact feedback linearization for bi-directional DC converter in DC microgrid[J]. Power System Protection and Control, 2018, 46(2): 43-49.
[本文引用: 2]
[16]
张丹, 王杰, 弥潇. 直流微电网自适应滑模控制策略[J]. 电力自动化设备, 2017, 37(12): 138-143+217.
[本文引用: 1]
ZHANG Dan, WANG Jie, MI Xiao. Adaptive sliding mode control strategy for DC microgrid[J]. Electric Power Automation Equipment, 2017, 37(12): 138-143+217.
[本文引用: 1]
[17]
罗玮,陆益民.带恒功率负载的Boost变换器模糊自适应反步滑模控制[J/OL].电源学报 [2021-10-16]. http://kns.cnki.net/kcms/detail/12.1420.TM.20210813.1640.002.html.
[本文引用: 1]
LUO Wei, LU Yimin. Fuzzy adaptive back-stepping sliding mode control of boost converter with constant Power Load[J/OL]. Journal of Power Supply, [2021-10-16]. http://kns.cnki.net/kcms/detail/12.1420.TM.20210813.1640.002.html.
[本文引用: 1]
[18]
XU D Z, DAI Y C, YANG C S, et al. Adaptive fuzzy sliding mode command-filtered backstepping control for islanded PV microgrid with energy storage system[J]. Journal of the Franklin Institute, 2019, 356(4): 1880-1898.
[本文引用: 1]
[19]
ROY T K, MAHMUD M A. Active power control of three-phase grid-connected solar PV systems using a robust nonlinear adaptive backstepping approach[J]. Solar Energy, 2017, 153: 64-76.
[本文引用: 1]
[20]
YU C J, JIANG J, ZHEN Z Y, et al. Adaptive backstepping control for air-breathing hypersonic vehicle subject to mismatched uncertainties[J]. Aerospace Science and Technology, 2020, 107: 106244.
[本文引用: 1]
[21]
WANG F, WANG J M, WANG K, et al. Adaptive backstepping sliding mode control of uncertain semi-strict nonlinear systems and application to permanent magnet synchronous motor[J]. Journal of Systems Science and Complexity, 2021, 34(2): 552-571.
[本文引用: 1]
[22]
XU Q W, VAFAMAND N, CHEN L L, et al. Review on advanced control technologies for bidirectional DC/DC converters in DC microgrids[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(2): 1205-1221.
[本文引用: 1]
[23]
熊然, 王顺利, 于春梅, 等. 基于Thevenin模型和改进扩展卡尔曼的特种机器人锂离子电池SOC估算方法[J]. 储能科学与技术, 2021, 10(2): 695-704.
[本文引用: 1]
XIONG R, WANG S L, YU C M, et al. An estimation method for lithium-ion battery SOC of special robots based on Thevenin model and improved extended Kalman[J]. Energy Storage Science and Technology, 2021, 10(2): 695-704.
[本文引用: 1]
[24]
刘新天, 何耀, 曾国建, 等. 考虑温度影响的锂电池功率状态估计[J]. 电工技术学报, 2016, 31(13): 155-163.
[本文引用: 1]
LIU X T, HE Y, ZENG G J, et al. State-of-power estimation for Li-ion battery considering the effect of temperature[J]. Transactions of China Electrotechnical Society, 2016, 31(13): 155-163.
[本文引用: 1]
[25]
朱阳. 不确定系统的自适应反步控制[D]. 杭州: 浙江大学, 2015.
[本文引用: 1]
ZHU Y. Adaptive backstepping control of uncertain systems[D]. Hangzhou: Zhejiang University, 2015.
[本文引用: 1]
[26]
王划一, 杨西侠. 现代控制理论基础[M]. 2版. 北京: 国防工业出版社, 2015: 280-281.
[本文引用: 1]
WANG H Y, YANG X X. Fundamentals of modern control theory[M]. 2nd ed. Beijing: National Defense Industry Press, 2015: 280-281.
[本文引用: 1]
1
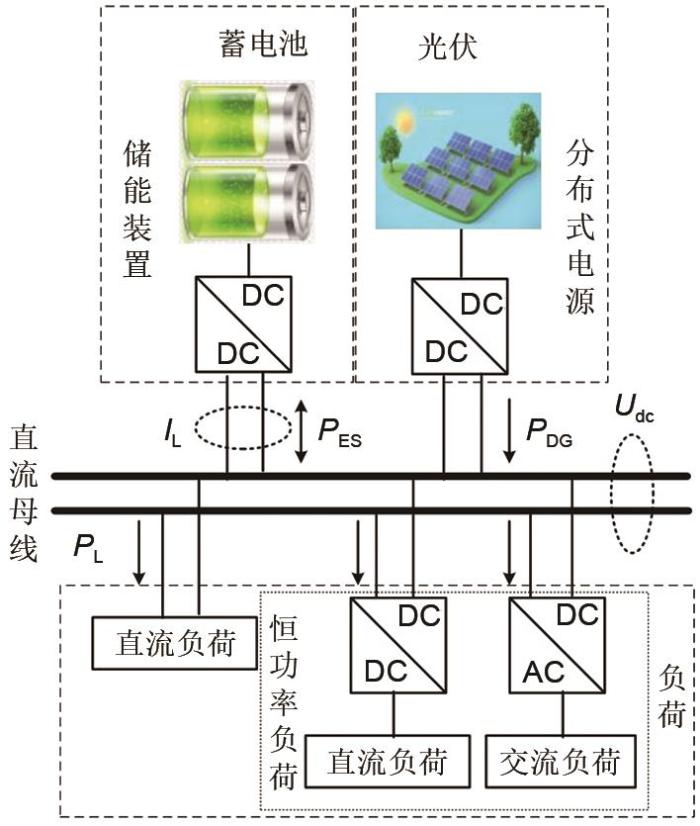
... “碳中和”和“碳达峰”目标的提出,必将促进能源领域的技术变革,加速能源利用由化石能源向以风力、光伏为代表的低碳清洁能源的转变.微电网是由分布式电源、储能系统、能量转换装置、相关负荷、监控和保护装置等汇集而成的小型发配电系统[1 ] ,是有效利用分布式清洁能源、实现低碳排放的重要举措之一.直流微电网因结构简单、节能高效、控制灵活等特点比交流和混合微电网更加受到关注. ...
1
... “碳中和”和“碳达峰”目标的提出,必将促进能源领域的技术变革,加速能源利用由化石能源向以风力、光伏为代表的低碳清洁能源的转变.微电网是由分布式电源、储能系统、能量转换装置、相关负荷、监控和保护装置等汇集而成的小型发配电系统[1 ] ,是有效利用分布式清洁能源、实现低碳排放的重要举措之一.直流微电网因结构简单、节能高效、控制灵活等特点比交流和混合微电网更加受到关注. ...
1
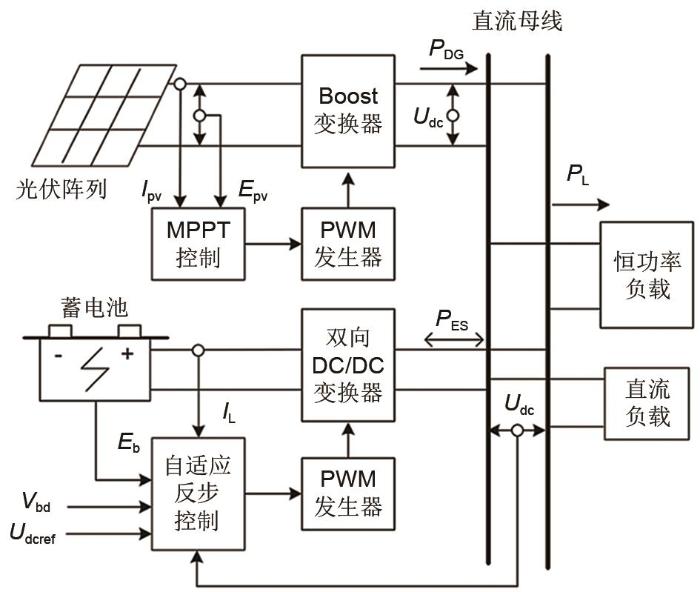
... 直流微电网中,母线电压是体现系统稳定的唯一指标,母线电压稳定与否代表系统瞬时能量是否平衡.影响直流微电网母线电压稳定的因素主要有:分布式电源的功率波动及投切、负荷波动及投切和交直流微电网间能量交换等[2 ] .直流母线电压如果失稳,会引起保护装置动作,严重时会导致整个系统崩溃.对于不与大电网相连的孤岛型直流微电网,在遭遇源、荷突变,或为恒功率负载供电时[3 ] ,上述问题尤为突出.对于此类母线电压波动现象,多通过电力电子变换器控制储能装置切换充放电模式,平抑光伏波动和负荷波动,实现直流微电网源、荷间的功率平衡,提高负荷供电可靠性[4 ] . ...
1
... 直流微电网中,母线电压是体现系统稳定的唯一指标,母线电压稳定与否代表系统瞬时能量是否平衡.影响直流微电网母线电压稳定的因素主要有:分布式电源的功率波动及投切、负荷波动及投切和交直流微电网间能量交换等[2 ] .直流母线电压如果失稳,会引起保护装置动作,严重时会导致整个系统崩溃.对于不与大电网相连的孤岛型直流微电网,在遭遇源、荷突变,或为恒功率负载供电时[3 ] ,上述问题尤为突出.对于此类母线电压波动现象,多通过电力电子变换器控制储能装置切换充放电模式,平抑光伏波动和负荷波动,实现直流微电网源、荷间的功率平衡,提高负荷供电可靠性[4 ] . ...
1
... 直流微电网中,母线电压是体现系统稳定的唯一指标,母线电压稳定与否代表系统瞬时能量是否平衡.影响直流微电网母线电压稳定的因素主要有:分布式电源的功率波动及投切、负荷波动及投切和交直流微电网间能量交换等[2 ] .直流母线电压如果失稳,会引起保护装置动作,严重时会导致整个系统崩溃.对于不与大电网相连的孤岛型直流微电网,在遭遇源、荷突变,或为恒功率负载供电时[3 ] ,上述问题尤为突出.对于此类母线电压波动现象,多通过电力电子变换器控制储能装置切换充放电模式,平抑光伏波动和负荷波动,实现直流微电网源、荷间的功率平衡,提高负荷供电可靠性[4 ] . ...
1
... 直流微电网中,母线电压是体现系统稳定的唯一指标,母线电压稳定与否代表系统瞬时能量是否平衡.影响直流微电网母线电压稳定的因素主要有:分布式电源的功率波动及投切、负荷波动及投切和交直流微电网间能量交换等[2 ] .直流母线电压如果失稳,会引起保护装置动作,严重时会导致整个系统崩溃.对于不与大电网相连的孤岛型直流微电网,在遭遇源、荷突变,或为恒功率负载供电时[3 ] ,上述问题尤为突出.对于此类母线电压波动现象,多通过电力电子变换器控制储能装置切换充放电模式,平抑光伏波动和负荷波动,实现直流微电网源、荷间的功率平衡,提高负荷供电可靠性[4 ] . ...
1
... 直流微电网中,母线电压是体现系统稳定的唯一指标,母线电压稳定与否代表系统瞬时能量是否平衡.影响直流微电网母线电压稳定的因素主要有:分布式电源的功率波动及投切、负荷波动及投切和交直流微电网间能量交换等[2 ] .直流母线电压如果失稳,会引起保护装置动作,严重时会导致整个系统崩溃.对于不与大电网相连的孤岛型直流微电网,在遭遇源、荷突变,或为恒功率负载供电时[3 ] ,上述问题尤为突出.对于此类母线电压波动现象,多通过电力电子变换器控制储能装置切换充放电模式,平抑光伏波动和负荷波动,实现直流微电网源、荷间的功率平衡,提高负荷供电可靠性[4 ] . ...
1
... 直流微电网中,母线电压是体现系统稳定的唯一指标,母线电压稳定与否代表系统瞬时能量是否平衡.影响直流微电网母线电压稳定的因素主要有:分布式电源的功率波动及投切、负荷波动及投切和交直流微电网间能量交换等[2 ] .直流母线电压如果失稳,会引起保护装置动作,严重时会导致整个系统崩溃.对于不与大电网相连的孤岛型直流微电网,在遭遇源、荷突变,或为恒功率负载供电时[3 ] ,上述问题尤为突出.对于此类母线电压波动现象,多通过电力电子变换器控制储能装置切换充放电模式,平抑光伏波动和负荷波动,实现直流微电网源、荷间的功率平衡,提高负荷供电可靠性[4 ] . ...
1
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
1
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
1
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
1
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
1
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
1
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
1
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
1
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
1
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
1
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
1
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
3
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
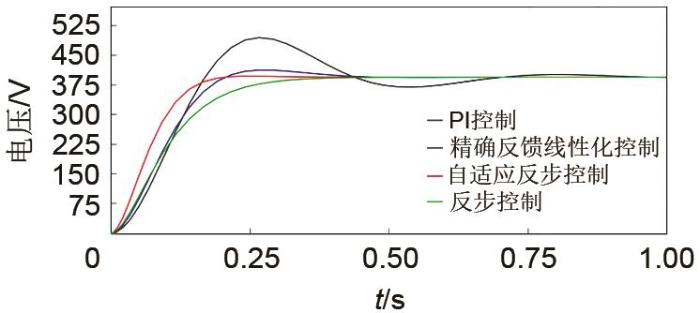
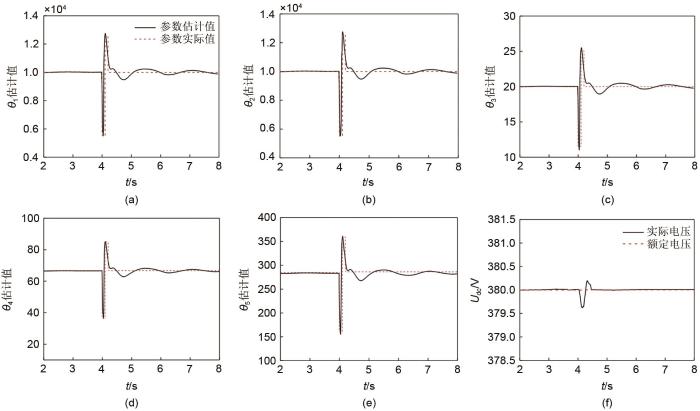
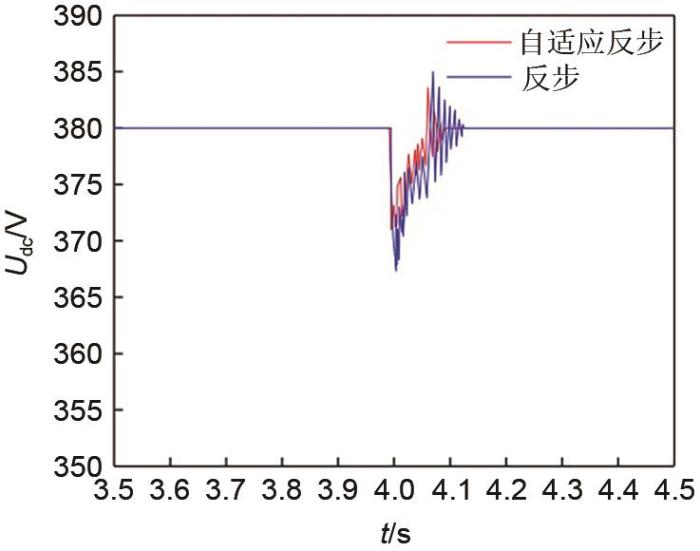
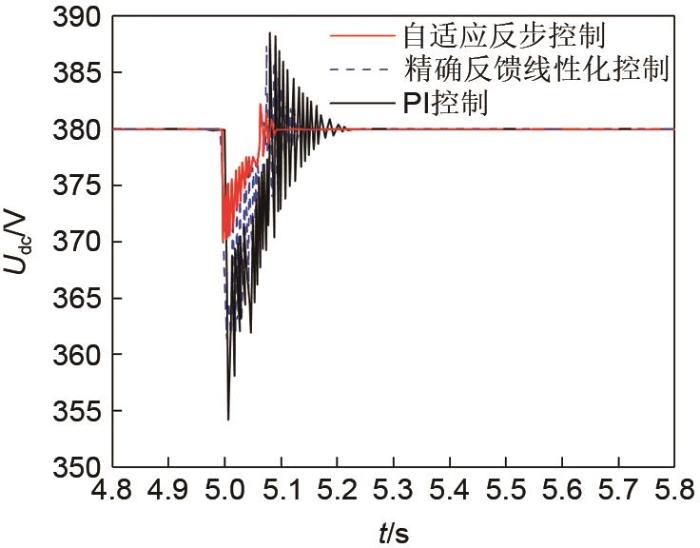
... 可知当参数估计误差为零时,即未知参数能被准确跟踪,则η = 2 k 1 e 1 2 + k 2 e 2 2 + k 3 e 3 2 e 1 2 + e 2 2 + e 3 2 k i [13 ] 和基于精确反馈线性化控制[15 ] 的系统快速性指标分别为:η 1 = 60 η 2 = 20 . ...
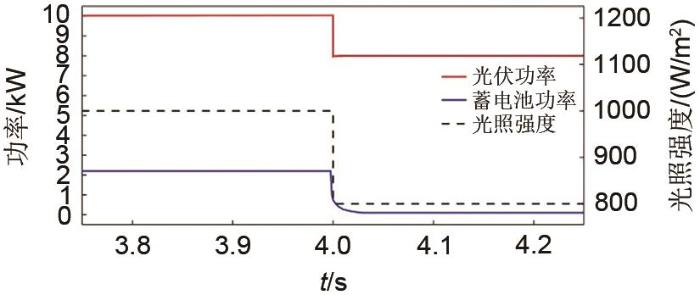
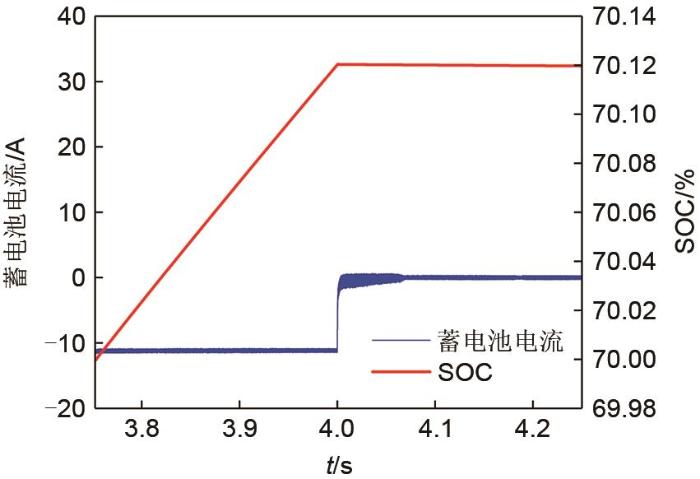
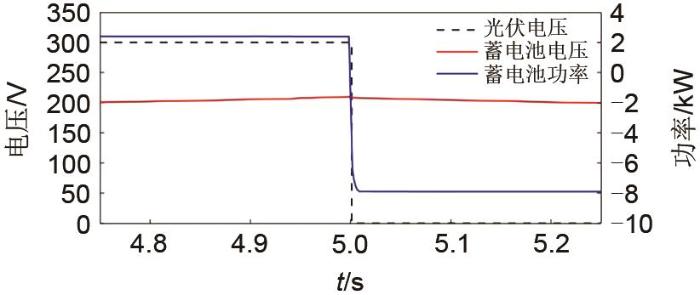
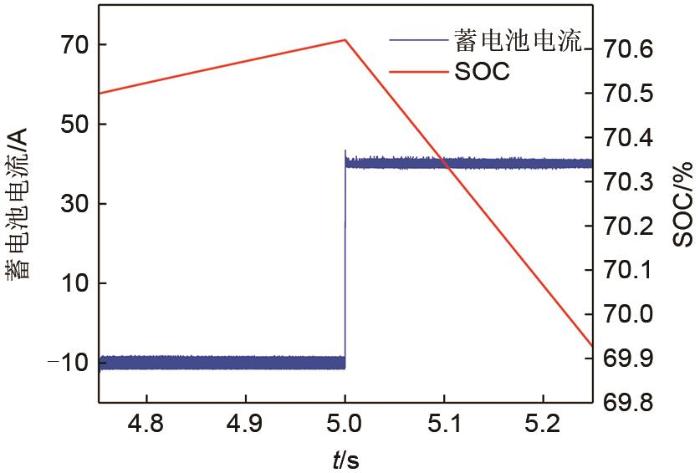
... 在上述调节过程中,0~4 s内,SOC持续增加至70.12%,4 s时,蓄电池电流约由-10.5 A变为0 A,SOC先增加后保持不变.由于蓄电池状态切换存在的惯性,直流微电网因瞬时功率不平衡而导致母线电压波动,如图12 所示.在本文设计的自适应反步控制器调节下,直流母线电压在371~385 V波动,最大电压偏差为2.4%,经过0.08 s,恢复380 V并保持稳定.与之相比,若控制器不具有参数自适应能力[13 ] ,母线电压将在368~386 V范围波动,最大电压偏差为3.2%,需经过0.12 s恢复380 V并保持稳定.因此,在本文所设计的自适应反步控制器调节下,母线电压响应速度较快,波动较小,控制效果较好. ...
3
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
... 可知当参数估计误差为零时,即未知参数能被准确跟踪,则η = 2 k 1 e 1 2 + k 2 e 2 2 + k 3 e 3 2 e 1 2 + e 2 2 + e 3 2 k i [13 ] 和基于精确反馈线性化控制[15 ] 的系统快速性指标分别为:η 1 = 60 η 2 = 20 . ...
... 在上述调节过程中,0~4 s内,SOC持续增加至70.12%,4 s时,蓄电池电流约由-10.5 A变为0 A,SOC先增加后保持不变.由于蓄电池状态切换存在的惯性,直流微电网因瞬时功率不平衡而导致母线电压波动,如图12 所示.在本文设计的自适应反步控制器调节下,直流母线电压在371~385 V波动,最大电压偏差为2.4%,经过0.08 s,恢复380 V并保持稳定.与之相比,若控制器不具有参数自适应能力[13 ] ,母线电压将在368~386 V范围波动,最大电压偏差为3.2%,需经过0.12 s恢复380 V并保持稳定.因此,在本文所设计的自适应反步控制器调节下,母线电压响应速度较快,波动较小,控制效果较好. ...
1
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
2
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
... 可知当参数估计误差为零时,即未知参数能被准确跟踪,则η = 2 k 1 e 1 2 + k 2 e 2 2 + k 3 e 3 2 e 1 2 + e 2 2 + e 3 2 k i [13 ] 和基于精确反馈线性化控制[15 ] 的系统快速性指标分别为:η 1 = 60 η 2 = 20 . ...
2
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
... 可知当参数估计误差为零时,即未知参数能被准确跟踪,则η = 2 k 1 e 1 2 + k 2 e 2 2 + k 3 e 3 2 e 1 2 + e 2 2 + e 3 2 k i [13 ] 和基于精确反馈线性化控制[15 ] 的系统快速性指标分别为:η 1 = 60 η 2 = 20 . ...
1
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
1
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
1
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
1
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
1
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
1
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
1
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
1
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
1
... 由于直流微电网中包含许多具有非线性特征的电力电子变换单元,因而整个系统存在很强的非线性和时变特性[5 -6 ] .因此,非线性、参数不确定等问题也成为储能装置变换器控制要考虑的关键因素,而传统基于小信号偏差线性化方法设计的线性控制器存在较大的局限性[7 -8 ] .为了解决以上问题,非线性设计方法被应用到储能装置控制器的设计中,包括精确反馈线性化(exact feedback linearization,EFL)控制,滑模变结构(sliding mode variable structure,SMVS)控制和反步(backstepping)控制等[9 ] .文献[10 ]基于精确反馈线性化方法设计的储能装置控制器表现了良好的性能,但该方法只针对特定系统模型和特定条件,对于一般的系统不易满足.文献[11 -12 ]分别对升压变换器和双向变换器设计滑模控制器来调节直流母线电压,控制易于实现,鲁棒性强,但稳定系统的同时伴随抖振问题,且时变滑模面非常难以选择,不易获得不确定性边界,不能在工程中广泛应用,取而代之的是反步控制.文献[13 ]针对储能变换器设计了反步控制器,在直流微电网系统输入端存在波动时能够有效维持母线电压稳定.文献[14 ]设计了混合储能系统积分反步控制器,保证了变功率发电下的功率平衡.但上述设计过程均假设系统中的储能电感、滤波电容等参数固定不变.当这些参数摄动时,控制器对参数变化和外界干扰的敏感性较低,控制效果不理想,鲁棒性差.为更好地控制非线性系统的稳定运行,提高系统鲁棒性,学者尝试将各类非线性方法互相结合.文献[15 ]将精确反馈线性化和反步滑模技术相结合运用于双向直流变换器设计中,使得系统在参数摄动和外部干扰情况下的鲁棒性和稳定性得到保证,但未考虑储能内部参数变化.文献[16 ]提出自适应全局滑模控制方法,在参数不确定及外部扰动下仅确保了简单微电网的稳定性和动态性能.文献[17 ]对Boost变换器提出一种模糊自适应反步滑模控制策略,获得了良好的动态调节性能和较强鲁棒性,但未应用于直流微电网.文献[18 -19 ]采用自适应反步方法对光伏并网逆变器设计了控制器,实现了光伏系统元件参数的在线辨识,保证了与电网有功率交换时的鲁棒性.文献[20 ]将自适应反步方法直接应用于飞行控制器设计,能够有效地补偿不确定参数,保证良好跟踪性能.文献[21 ]针对一类含未知参数和不确定性扰动的半严格非线性系统,采用自适应技术有效处理参数未知和不确定性的问题,应用于永磁同步电机并获得了良好控制性能.可以看出,对于处理模型的不确定性,反步方法和自适应估计技术组成的复合解决方案可以实现快速准确的动态跟踪,且保证大信号的稳定性[22 ] ,因此有必要将其应用于储能装置变换器的控制. ...
1
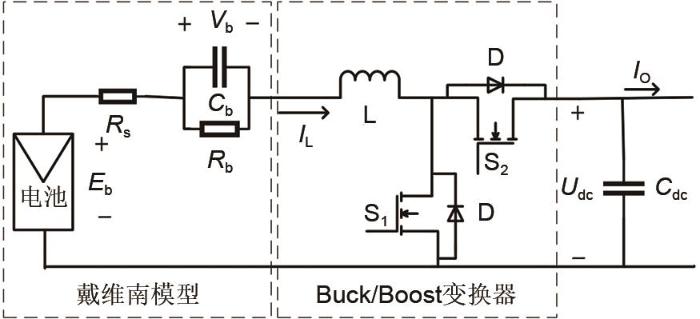
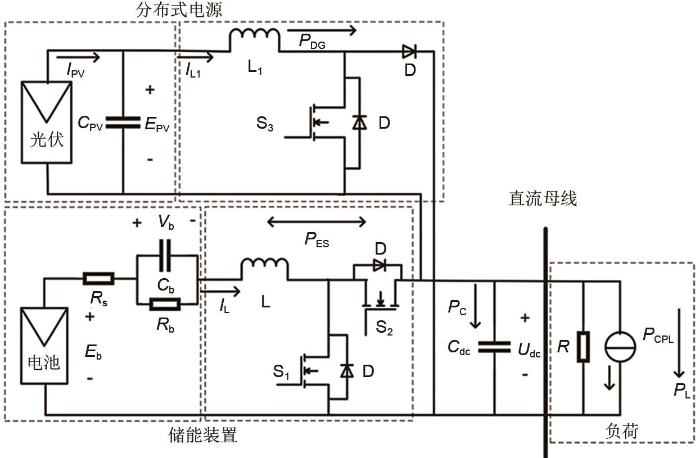
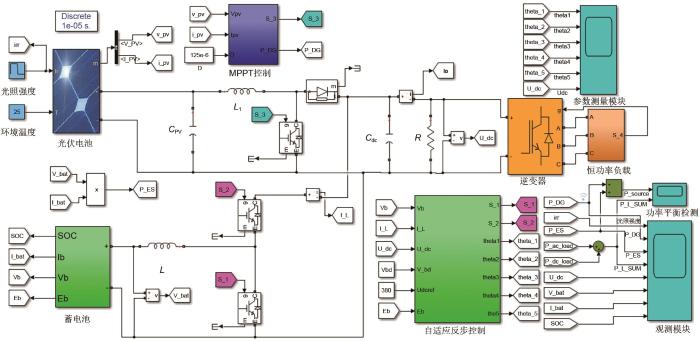
... 光伏阵列由多个单体光伏电池串并联构成,以满足分布式电源供电需求.在孤岛运行模式下,当光照不足或负荷不足的情况下,直流微电网需要储能装置平衡能量差额.蓄电池是一种电化学储能装置,常用的等效电路是戴维南模型[23 ] . ...
1
... 光伏阵列由多个单体光伏电池串并联构成,以满足分布式电源供电需求.在孤岛运行模式下,当光照不足或负荷不足的情况下,直流微电网需要储能装置平衡能量差额.蓄电池是一种电化学储能装置,常用的等效电路是戴维南模型[23 ] . ...
1
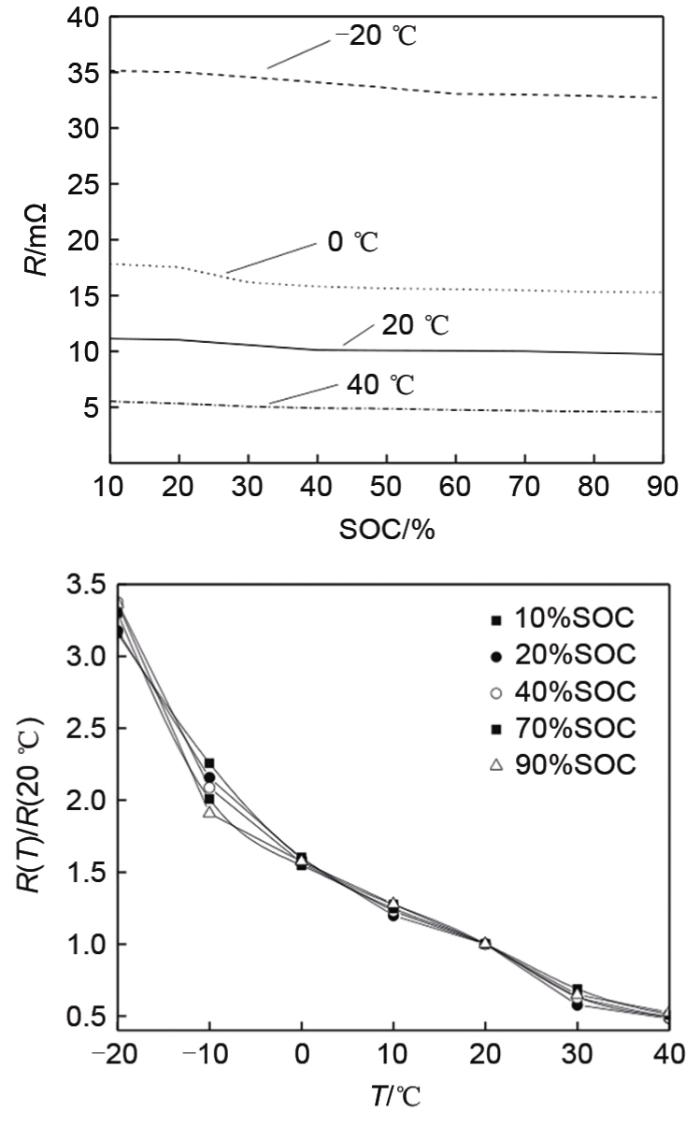
... 戴维南模型将蓄电池的内阻、过电压电阻与电容等参数都设定成了固定的常数.而在实际应用中,各参数与荷电状态(state of charge,SOC)、温度以及电解液的密度都有密切关系,其值是时变的.例如,锂电池内阻随SOC和温度变化情况如图2 所示[24 ] . ...
1
... 戴维南模型将蓄电池的内阻、过电压电阻与电容等参数都设定成了固定的常数.而在实际应用中,各参数与荷电状态(state of charge,SOC)、温度以及电解液的密度都有密切关系,其值是时变的.例如,锂电池内阻随SOC和温度变化情况如图2 所示[24 ] . ...
1
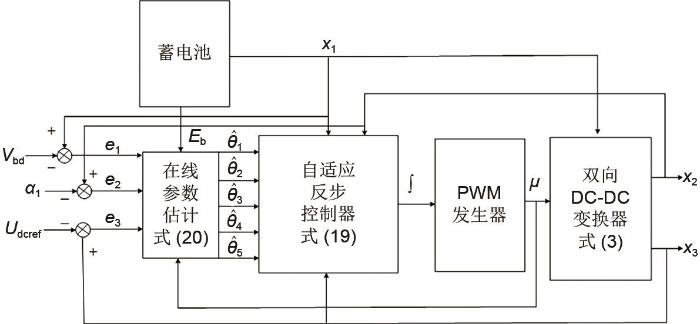
... 反步控制是将高阶非线性系统分解为低阶子系统,从而针对每个子系统选取Lyapunov函数和设计虚拟控制输入,直至“后退”到整个系统,最后将每个子系统的Lyapunov函数和虚拟控制输入进行集成来完成总控制律的设计.自适应反步法是在反步设计的基础上把设计中处理不确定参数的自适应函数和镇定函数联系起来,逐步修正算法设计镇定控制器,最终实现系统的全局调节或跟踪,达到期望的性能指标.具体设计原理请参考文献[25 ]. ...
1
... 反步控制是将高阶非线性系统分解为低阶子系统,从而针对每个子系统选取Lyapunov函数和设计虚拟控制输入,直至“后退”到整个系统,最后将每个子系统的Lyapunov函数和虚拟控制输入进行集成来完成总控制律的设计.自适应反步法是在反步设计的基础上把设计中处理不确定参数的自适应函数和镇定函数联系起来,逐步修正算法设计镇定控制器,最终实现系统的全局调节或跟踪,达到期望的性能指标.具体设计原理请参考文献[25 ]. ...
1
... Lyapunov函数V ( x ) x x x e = 0 V ˙ ( x ) < 0 x [26 ] : ...
1
... Lyapunov函数V ( x ) x x x e = 0 V ˙ ( x ) < 0 x [26 ] : ...