目前针对系统中的不确定性问题研究主要从源、荷单侧或源-荷双侧同时考虑几个角度展开[13-15]。文献[16]针对可再生能源高渗透率电力系统,提出了一种考虑源、荷随机性的电-氢综合能源系统两阶段规划模型;文献[17]考虑风光出力和电动汽车充电负荷的源、荷双侧不确定性,对风-光-氢综合能源系统进行容量规划;文献[18]设计了应用可逆固体氧化物电池的电-氢一体化能源站框架,并采用考虑源、荷不确定性的随机规划方法对能源站内各装置进行容量配置。以上对电-氢混合系统面临的不确定性问题研究,仅考虑了系统面临的短期不确定性,并未充分考虑气候、经济等因素对源、荷双侧随机变量的长期影响,即源、荷双侧的长期不确定性。
随着电-氢一体化储能站使用年限的增长,基于历史数据得到的概率密度函数难以准确描述随机变量的实际概率分布,因此仅考虑短期不确定性的常规随机规划(stochastic programming,SP)无法规避长期不确定性的影响。基于非概率又非模糊的信息间隙决策理论(information gap decision theory,IGDT)的鲁棒优化方法可用来处理源、荷双侧的长期不确定性[19]。对比传统鲁棒优化方法和随机规划,IGDT无须准确描述不确定变量波动范围和其概率分布,在不确定性变量信息较少时即可最大化其波动区间,进而规避长期不确定性带来的风险。
常规IGDT理论考虑随机变量的短期不确定性,导致其规划结果经济性不足。因此,结合SP与IGDT理论规划方法的优点,提出一种计及源、荷双侧多时间尺度不确定性的储能站随机-鲁棒混合规划方法。在新能源高渗透率电力系统中,对电-氢一体化储能站主要装置容量规划开展研究。首先,考虑源、荷的短期不确定性,随机生成全年源、荷序列,并运用最优分割法和考虑场景间相似度指标的动态时间规整(dynamic time warping,DTW)算法进行场景提取,得到更符合实际情况的时序典型场景;然后,依据电-氢一体化储能站运行模式,构建储能站的容量规划模型,并进一步考虑长期不确定性,采用SP-IGDT混合规划方法,建立计及多尺度不确定性的电-氢一体化储能站随机-鲁棒混合规划模型;最后,基于某风光电场进行算例分析,验证所提规划方法的有效性。
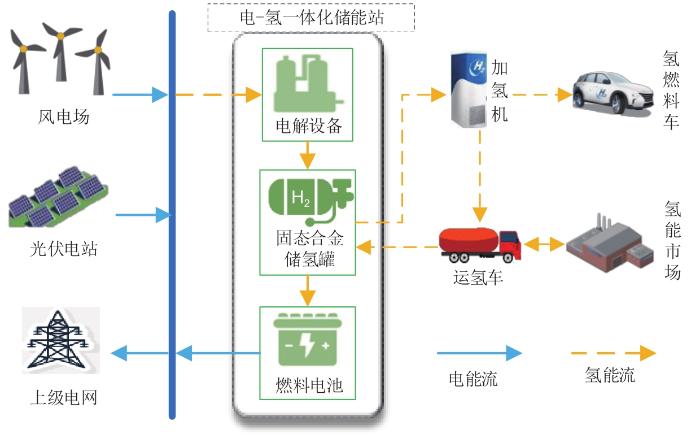
1 电-氢一体化储能站结构
电-氢一体化储能站是立足于发电侧,可与新能源发电站共同组成电-氢混合能源系统,图1为电-氢混合系统基本结构。
图1
根据储氢系统可在电、氢能量之间灵活转换的特点,电-氢一体化储能站的运行模式如下。
(1)围绕系统中电能流:储能站可以通过电转氢(power to hydrogen,P2H)装置,充分发挥氢储能的优势,适应风、光出力和电、氢负荷需求的长期不确定性,保障系统能源供需平衡与稳定运行。
(2)围绕系统中氢能流:储能站可向氢燃料汽车供应氢气或在氢能市场进行氢气销售,丰富氢能利用模式,提高储能站经济效益与氢能的利用率;储能站也可在氢气储量不足时,直接从氢能市场购氢,避免因能量供应不足导致惩罚成本增加。
储氢装置、电解槽和燃料电池为电-氢一体化储能站核心装置,其主要装置种类如下。
(1)固态储氢罐
表1 不同储氢方式主要特性
Table 1
| 类型 | 高压气态储氢 | 低温液态储氢 | 固态储氢 |
|---|---|---|---|
| 工作温度/℃ | -40~85 | <-253 | -40~60 |
| 寿命/a | 15~20 | <10 | 15~30 |
| 储氢密度(质量分数)/% | 1~3 | >10 | 1~18 |
| 成本/(元/kg) | 4000~7000 | 11000~15000 | 8000~11000 |
(2)能量转换装置
相较于碱性电解装置,质子交换膜电解槽响应时间短、电流密度大、体积更加紧凑,更适合用于集成0~100 MW超大规模系统[20],因此选用质子交换膜电解槽作为电解制氢装置。
新能源出力以及电、氢负荷需求存在较强的随机性问题,在出力充足时段,储能站可通过电解装置将电能转换为氢能;在电负荷供应不足时段,可通过燃料电池将氢能转化为电能;在氢负荷需求高峰时段,储能站也可通过“电解设备实时制氢+储氢罐放氢”的方式满足氢负荷需求。通过以上运行策略,可实现日内尺度的电能、氢能的削峰填谷以及可再生能源的跨季节转移,提高可再生能源的消纳水平。
2 计及多时间尺度不确定性的储能站随机-鲁棒混合规划方法
2.1 源-荷典型场景提取
采用基于多场景的随机规划来描述电-氢混合系统的短期不确定性,为获取更加符合实际情况的典型日场景,需要考虑风、光、电-氢负荷的时序相关特性,而DTW能够更好地刻画时间序列的整体动态特性,辨别曲线间的相似度。因此,运用最优分割法和计及源-荷间相关性的DTW算法提取源-荷时序典型场景[22],以弥补传统聚类方法对整体时序特性描述的不足。
考虑到风、光等新能源出力的随机性较强,而负荷需求存在明显的周期性,因此将负荷功率作为最优分割基准。主要步骤如下。
(1)根据历史数据得到的概率分布,生成全年源、荷运行序列,采用最优分割法对负荷数据进行时序分段,并按负荷序列的时间分段点进一步分割,得到不同季节中风、光、电、氢的典型时序场景集。
(2)生成源-荷序列的时序相关性曲线,计算源荷序列的欧氏距离θ,场景内源-荷相关性矩阵 Y 以及DTW距离矩阵 D,如式(
式中,α、β分别为源、荷序列;di, j 为序列之间的DTW距离。
引入场景间相似度评价指标φ,以描述源荷序列的时序相关性与整体动态特性,如
式中,ρ1、ρ2、ρ3分别为欧氏距离、相关性矩阵以及DTW距离的权重系数。
(3)基于动态规划思想,采用考虑场景间相似度指标的DTW算法,得到时序相关的风-光-电-氢的联合时序典型场景,作为后续规划阶段的基础。
2.2 基于短期不确定性场景的储能站随机规划模型
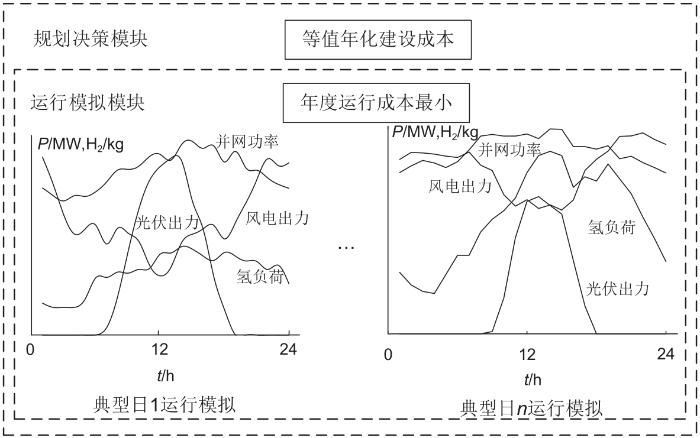
如图2所示,采用随机规划方法,构建基于短期不确定性场景的电-氢一体化储能站容量随机规划模型。其中,规划决策模块确定储能站各设备的额定容量;运行模拟模块采用随机规划方法,以年运行成本最小为目标,对储能站进行年度运行模拟。
图2
2.2.1 目标函数
电-氢一体化储能站容量规划模型的目标函数为电-氢混合系统的年综合成本C最小,包括等值年化建设成本Cinv、运维成本Com、弃风弃光成本Cp和缺能惩罚成本Ccut,如
(1)储能站等值年化建设成本。将储能站总建设成本折合成等值年化建设成本,如
式中,N为设备的种类数量,包括储氢罐、电解槽和燃料电池;Ei, d为第i种设备的容量;ci, d为第i种设备的单位成本;m为折现率,取0.1;y表示各设备的预期寿命,规划年限为20年。电解槽、燃料电池等设备的使用寿命相对较短,规划周期内的设备更替成本已折算至
(2)储能站运维成本。当风光电场出力无法满足其负荷需求时,电-氢一体化储能站通过燃料电池消耗氢气同时向电网供电。此时,如储能站氢气储量不足,则需从氢能市场外购氢气供应燃料电池发电,以满足风光电场的供电需求。因此其年度运维成本主要为购售氢成本和维护成本,如
式中,S为典型场景数;Ps 为第s种场景的概率;ch为氢气市场的售氢价格;Hbuy(t)、Hload(t)分别为t时刻储能站向氢能市场的购氢量和氢负荷需求;λi, d为第i种设备的维护成本系数。
(3)弃风弃光成本。若风光电场发出的电能无法完全消纳,则会产生一定的弃风、弃光成本,如
式中,Pwaste, w(t)、Pwaste, pv(t)分别为t时刻的弃风、弃光功率;cw、cpv分别为弃风、弃光单位成本。
(4)缺能惩罚成本。当储氢罐配置通量较小时,可能出现氢负荷与燃料电池氢气需求过大导致氢气供应不足。若此时仅依靠从氢能市场外购氢气以满足氢气需求,会导致储能站运行成本大幅增加,因此引入缺能惩罚成本来平衡电-氢系统运行成本和供能缺失。缺能惩罚成本主要包括失电惩罚成本和削氢惩罚成本,如
式中,Pshort(t)、Hcut(t)分别为t时刻的供电缺失功率、氢气削减量;cp, e、cp, h分别为单位失电惩罚成本、削氢惩罚成本。
2.2.2 约束条件
(1)电能平衡约束。为保持系统的稳定运行,电-氢混合系统中各设备功率需满足以下约束,如
式中,Pwt(t)、Ppv(t)、Pload(t)、Ped(t)、Pfc(t)分别为风光电场t时刻的风电出力、光伏出力、并网负荷需求、电解设备的耗电功率以及燃料电池的发电功率。
(2)能量转换装置功率约束。电解槽和燃料电池的转换过程如
式中,Hed(t)为t时刻电解设备的产氢速率;Hfc(t)为t时刻燃料电池的耗氢速率;ηed、ηfc分别为电解槽、燃料电池的能量转化效率;Bed(t)、Bfc(t)为0-1变量,分别表示t时刻电解设备和燃料电池的工作状态,其中0表示设备处于停机状态,1表示设备处于工作状态。
储能站的储氢和用氢的功率不能大于其额定功率且电解槽和燃料电池不能同时处于运行状态。因此电解槽和燃料电池有以下约束,如
式中,Ped,max、Pfc,max分别为电解槽、燃料电池的额定功率;Ped,min、Pfc,min分别为电解槽、燃料电池的最小运行功率。
(3)弃风弃光量约束。依据新能源可持续发展政策,弃风弃光量需满足一定的上限约束,如
式中,βw为弃风弃光量上限。
(4)储氢罐容量约束。首先,为保证在系统初始运行时刻,储能站可进行储氢或放氢操作,储氢罐中已有初始储量;其次,氢气储量不能超过储氢罐的规划容量。因此,储氢罐容量约束如
式中,SHS(t)、SHS, max分别为固态储氢罐的t时刻储氢质量和额定储氢质量。
(5)氢能平衡约束。在电-氢一体化储能站中,电解槽、燃料电池所生产或消耗的氢气与氢负荷以及氢气削减量之间需满足氢能平衡约束,如
式中,Hload(t)为t时刻储能站的氢负荷需求。
(6)固态储氢罐寿命约束。固态储氢材料受其使用寿命限制,在吸放氢循环过程中,储氢材料可能会发生氧化反应,使储氢罐的可逆储氢容量降低导致使用寿命缩减[23]。因此,固态储氢罐寿命主要与其吸氢总量有关,如
式中,yM为固态合金储氢罐的实际使用寿命;yM0为固态合金储氢罐的理想寿命;μ为常数;Qin为储氢合金的吸氢量。
2.3 考虑长-短期不确定性的随机-鲁棒混合规划模型
基于上述储能站随机规划模型,进一步引入IGDT的风险规避策略,保证规划结果不劣于预期投资的条件下,最大程度规避源、荷长期不确定性的影响。
在IGDT鲁棒规划模型中,源、荷双侧不确定性变量集合γ如
式中,γ为不确定性变量,包括风、光出力以及电、氢负荷需求实际值;
结合2.2节建立的电-氢一体化储能站容量规划模型,可得到基于IGDT风险规避策略下的储能站鲁棒规划模型如
式中,
由于IGDT理论在处理多个不确定性变量时,会导致规划模型的目标数增加,使模型复杂度增加。因此,本工作采用半径线性加权归一法将风电、光伏出力和电、氢负荷需求等不确定性变量,转化为其共同作用下的等效偏差半径,如
式中,rran为等效偏差半径,其值越大表示规划方案所能承受的不确定性变量波动范围越大;kw、kp、kl、kh分别为风电出力、光伏出力、电负荷和氢负荷的偏差半径的权重,根据实际配置需求利用判断矩阵法确定,以反映投资者对风、光、荷不确定性的重视程度。
综上所述,考虑源-荷双侧存在的长短期不确定性,基于SP-IGDT的电-氢一体化储能站随机-鲁棒混合规划模型如
2.4 模型求解流程
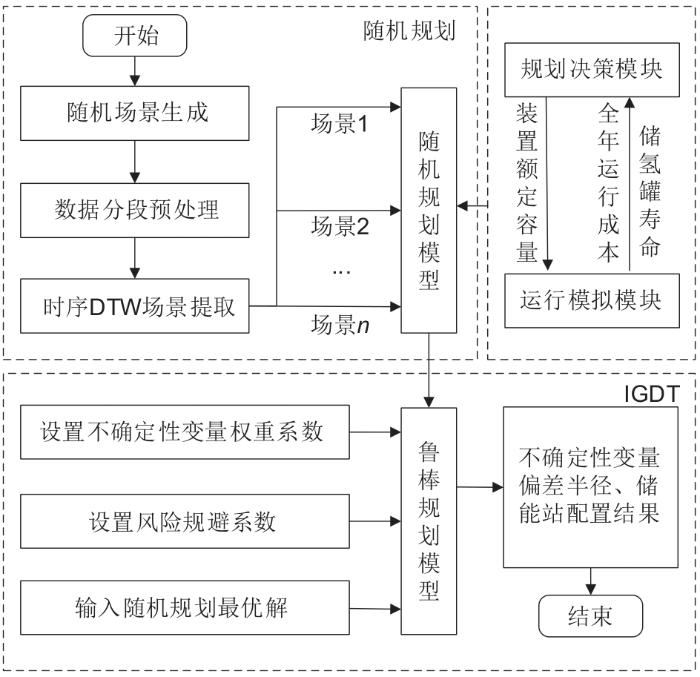
如图3所示,电-氢一体化储能站随机-鲁棒混合规划流程包括以下阶段。
图3
图3
储能站随机-鲁棒混合规划框架
Fig. 3
Stochastic-robust hybrid planning framework of energy storage stations
(1)SP随机规划阶段。包括以下步骤:
步骤1:式(
步骤2:以式(
(2)IGDT鲁棒规划阶段。基于随机规划阶段的初始规划方案与决策者设置的风险规避系数,对式(
3 算例分析
3.1 算例设置
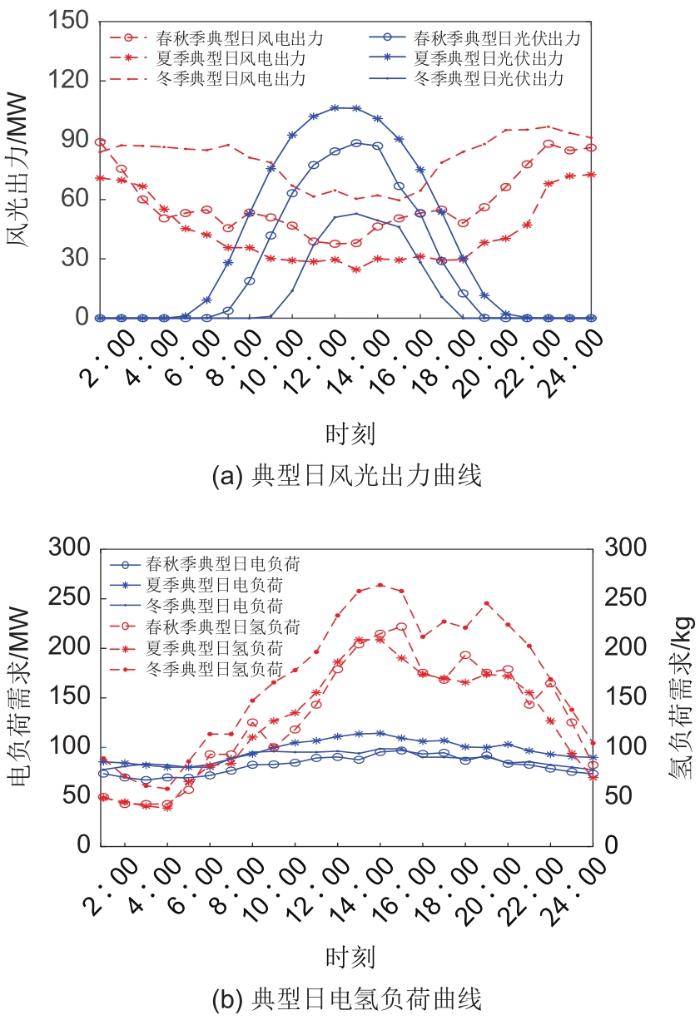
本工作以某风光电场为规划对象,该电场配置100 MW风电机组和120 MW光伏发电装置。参考当地历史天气及运行数据生成全年源、荷序列,借助考虑相关性距离的DTW算法进行分段聚类,得到春秋季、夏季和冬季的典型日数据序列,各典型日天数分别为162 d、91 d和112 d,如图4所示。
图4
表2 储能站各设备经济技术参数
Table 2
| 参数 | 数值 |
|---|---|
| 固态合金储氢罐单位成本/(元/kg) | 8000 |
| 电解槽单位成本/(万元/MW) | 200 |
| 燃料电池单位成本/(万元/MW) | 400 |
| 电解槽效率/% | 60 |
| 燃料电池效率/% | 65 |
| 运行维护成本系数 | 0.04 |
| 弃风弃光成本/(元/MWh) | 360 |
| 失电惩罚成本/(元/MWh) | 2000 |
| 削氢惩罚成本/(元/kg) | 150 |
3.2 储能站规划结果
3.2.1 储能站设备规划容量
基于经验值,风险规避系数取值0.1,各不确定性变量占比均取值0.25,采用MATLAB R2018b中的YALMIP/CPLEX12.8商用求解器对基于SP-IGDT储能站随机-鲁棒规划模型进行求解,得到最优规划方案见表3,表中基于多场景法的随机规划模型为仅考虑短期不确定的规划模型,即为IGDT鲁棒规划中确定性模型。
表3 储能站规划结果
Table 3
| 规划模型 | 电解槽 /MW | 燃料电池 /MW | 固态储氢罐 /kg | 年综合成本 /万元 |
|---|---|---|---|---|
| 随机规划 | 34.2 | 32.3 | 3943 | 3737.24 |
| 随机-鲁棒规划 | 36.5 | 36.7 | 4100 | 4110.96 |
由表3可知,考虑长-短期不确定性随机-鲁棒混合规划模型的求解得到各设备规划容量与仅考虑短期不确定性的随机规划模型相比均有所增加。在随机规划模型下,决策者按照预测的源-荷典型场景对电-氢混合系统进行规划,相当于等效偏差半径为0。而在随机-鲁棒混合模型下,源、荷双侧的等效偏差半径为18.31%,可以理解为得到的规划方案在规划周期内能承受的源、荷双侧的最大波动范围为18.31%,即系统承受源、荷双侧长期不确定性的鲁棒水平是18.31%。此时决策者需承担规避系数为0.1的预算投资,即系统投资预算增加10%。因此,所提规划方法可更好应对储能站投入使用后面临的长期不确定性。
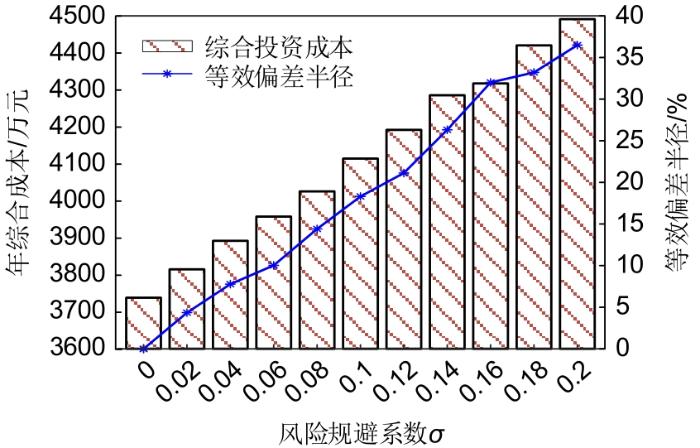
3.2.2 风险规避系数灵敏度分析
风险规避系数σ代表储能站规划者对其规划成本增加的接受程度,同时反映了配置方案对长期不确定性的应对能力。风险规避系数越大,规划者能接受的预算越高,规划方案对不确定性变量的适应程度越高,鲁棒性越强。
求解不同风险规避系数下的SP-IGDT随机-鲁棒模型,并分析其对年综合成本与等效偏差半径的影响。由图5可知,随着风险规避系数增大,规划方案能承受的风、光、电、氢等效偏差半径从0增加到36.49%,年综合成本也从3737.24万元增加到4485.17万元。等效偏差半径越大,表示电-氢混合系统的鲁棒性越强,能更好应对储能站投入运营后面临的源-荷长期不确定性。储能站规划方可根据自身承受投资成本上限、对负荷需求的保障程度以及系统稳定性需求来选择风险规避系数、风光电氢等不确定性变量的权重系数。
图5
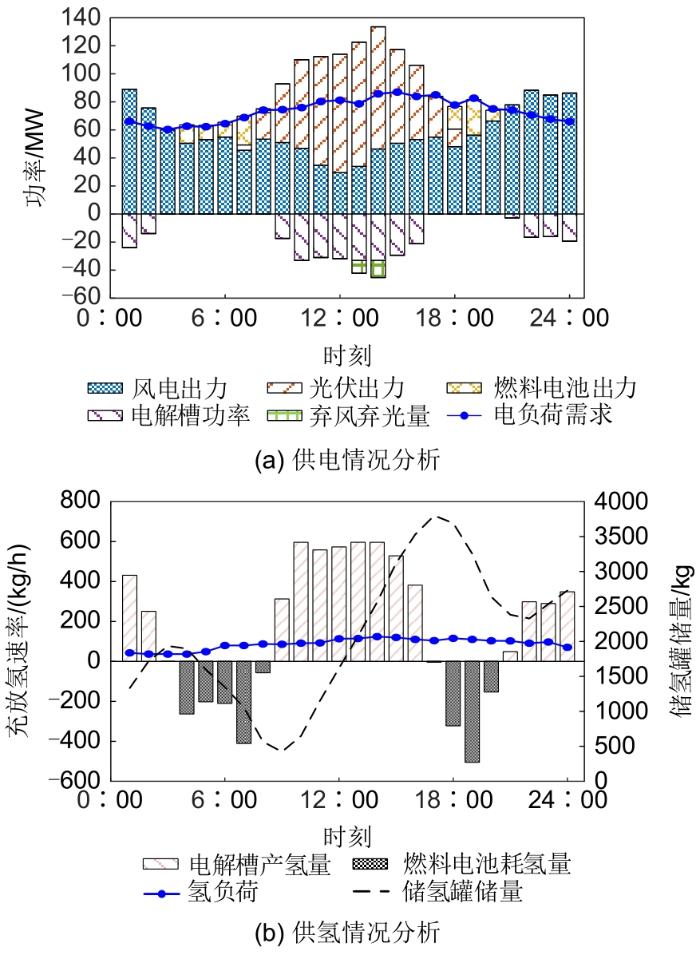
3.2.3 储能站运行工况分析
选取春秋季典型场景为例进行日运行工况分析,电能平衡和氢能平衡如图6所示。由图6(a)可知,储能站的电解槽在0:00—2:00、9:00—16:00和21:00—24:00这三个时段运行,以消纳风光电场的富余电能,此时电解槽制备的氢气可直接满足氢气负荷,富余氢气则存入储氢罐中。而在3:00—8:00和17:00—21:00时段,风光场站的联合出力已无法满足并网负荷需求,储氢罐释放氢气,以满足燃料电池发电并网和负荷的氢气需求。由图6(b)储氢量曲线可以看出,在春秋季典型日结束时刻,储氢罐储量相比初始运行时刻有较大程度增长,这是由于春秋季的风电、光伏资源均较为充足,储能站制氢量大于燃料电池发电和氢负荷供应的总氢气需求。其余典型日运行工况与春秋季典型日类似,在此不再赘述。
图6
此外,在春秋季典型日、夏季和冬季典型日,储能站均已基本消纳风光出力,仅在风光出力高峰时段,存在少量弃风弃光现象;同时在运行阶段均已满足负荷需求,并未出现电、氢负荷削减的情况。由此表明,配置电-氢一体化储能站的风光电场,具有更灵活的能量互动能力,可提高新能源利用率。
3.3 规划方法对比
表4 规划方法对比 (万元)
Table 4
| 成本 | 两阶段随机优化 | 常规IGDT | SP-IGDT |
|---|---|---|---|
| 年综合成本 | 3936.41 | 4346.77 | 4110.96 |
| 建设成本 | 24212.0 | 26709.6 | 25260.0 |
| 弃风弃光成本 | 114.23 | 51.21 | 55.35 |
| 失电惩罚成本 | 17.51 | 11.64 | 12.49 |
| 削氢惩罚成本 | 15.26 | 10.01 | 10.77 |
(1)与两阶段随机优化方法对比分析。采用SP-IGDT方法求解的年综合成本要高于两阶段随机优化的结果,主要体现在储能站建设成本上;而在模拟运行阶段,采用SP-IGDT方法规划的储能站能量利用率更高,其弃风弃光率和缺能率分别为后者的48.5%和70.9%,结果表明SP-IGDT法得到的规划结果具有更强的鲁棒性,更能适应电-氢系统面临的随机性。为有效应对新能源出力难以预测以及负荷需求长期增长等问题,电-氢一体化储能站需适当追加投资以增强其鲁棒性,进而规避源、荷双侧的长期不确定性,减少风光电场弃风弃光量、供电缺失能量以及氢负荷需求削减量。
(2)与常规IGDT方法对比分析。采用SP-IGDT方法得到的年综合成本明显小于常规IGDT,而在模拟运行阶段的成本略高于后者,二者的弃风弃光率与缺能率相对误差均在7%以内,表明两种方法规划的储能站应对不确定性的能力相近。这是由于SP-IGDT考虑了短期不确定性,将计及源-荷变量时序相关性的随机优化结果,作为其鲁棒规划的基础参数,使规划方案更具准确性与经济性。因此,采用基于SP-IGDT的储能站随机-鲁棒混合规划方法,其规划结果在保留常规IGDT鲁棒性的基础上,更具经济性。
总体上看,在计及多尺度不确定性的场景中,基于SP-IGDT的随机-鲁棒混合规划方法可兼顾储能站规划方案的经济性与鲁棒性。
3.4 经济灵敏度分析
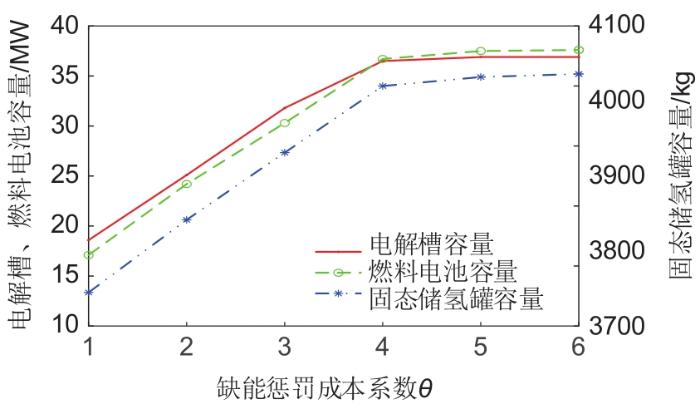
3.4.1 缺能惩罚成本系数灵敏度分析
图7
图7
缺能惩罚成本系数灵敏度分析
Fig. 7
Sensitivity analysis of energy deficiency penalty coefficient
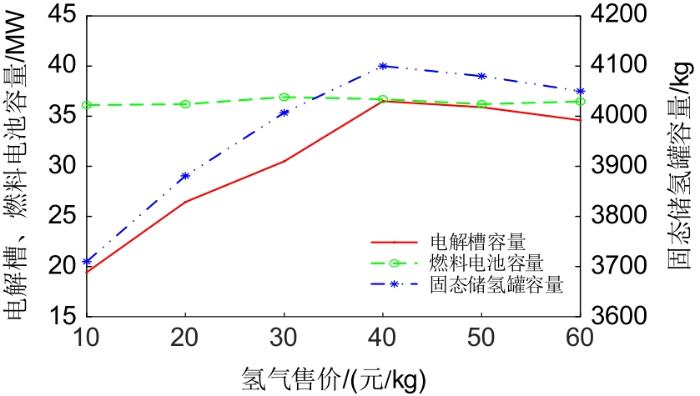
3.4.2 氢气售价灵敏度分析
氢气售价主要通过售氢收益和购氢成本来影响储能站的规划容量,图8为氢气售价灵敏度分析。由图8可知,当氢气售价较低时,电解槽和储氢罐的规划容量与氢气售价呈正相关。当氢气售价达到30元/kg时,电解槽和储氢罐容量增长趋势变缓;当氢气售价提高到40元/kg以上时,随着售价继续升高,电解槽和储氢罐的规划容量则开始下降,这是由于氢气售价过高导致氢负荷需求下降,使得储能站盈利能力受到抑制,难以收回储能站的建设成本、运维成本。燃料电池的规划容量基本保持不变,这是由于氢气售价主要从氢负荷盈利与外购氢气成本等角度对储能站规划产生影响,而燃料电池主要用于新能源低谷时供电,因此燃料电池规划容量对氢气售价的灵敏度较低。
图8
4 结论
针对电-氢一体化储能站规划问题开展研究,考虑源-荷的多时间尺度不确定性,提出基于SP-IGDT的随机-鲁棒混合规划方法,通过仿真分析对比,主要结论如下。
(1)考虑了长-短期不确定性的储能站规划方案,可有效应对源-荷双侧的随机性与波动性,降低了弃风弃光量和失能水平,提高了电-氢混合系统的能量利用率。
(2)采用计及多时间尺度不确定性的随机-鲁棒混合规划方法,考虑了短期不确定性以保证储能站规划方案的准确性与经济性,同时有效规避因随机变量长期不确定性无法准确描述导致的风险,保证规划方案的鲁棒性。通过与两阶段随机优化、常规IGDT等规划方法对比,所提规划方法能更好地兼顾规划方案的经济性与鲁棒性。
(3)对失能惩罚成本和氢气售价的灵敏度分析结果表明,电-氢一体化储能站的规划,应充分考虑失能惩罚成本和投资成本的平衡关系以及关注氢能市场的价格趋势,选择合理的失能惩罚成本系数和氢气售价,以获取最合理的规划方案。
参考文献