[1]
高铭琨, 徐海亮, 吴明铂. 基于等效电路模型的动力电池SOC估计方法综述[J]. 电气工程学报, 2021, 16(1): 90-102.
[本文引用: 1]
GAO M K, XU H L, WU M B. Review of SOC estimation methods for power battery based on equivalent circuit model[J]. Journal of Electrical Engineering, 2021, 16(1): 90-102.
[本文引用: 1]
[2]
陈海生,俞振华,刘为. 储能产业研究白皮书2021[R]. 中国能源研究会储能专委会/中关村储能产业技术联盟,2021.
[本文引用: 1]
CHEN H H, YU Z H, LIU W. White paper on energy storage industry research 2021[R]. China Energy Research Association Energy Storage Special Committee/Zhongguancun Energy Storage Industry Technology Alliance, 2021.
[本文引用: 1]
[3]
黄凯, 郭永芳, 李志刚. 动力锂离子电池荷电状态估计综述[J]. 电源技术, 2018, 42(9): 1398-1401.
[本文引用: 3]
HUANG K, GUO Y F, LI Z G. Review of state of charge estimation methods for power lithium-ion battery[J]. Chinese Journal of Power Sources, 2018, 42(9): 1398-1401.
[本文引用: 3]
[4]
付诗意, 吕桃林, 闵凡奇, 等. 电动汽车用锂离子电池SOC估算方法综述[J]. 储能科学与技术, 2021, 10(3): 1127-1136.
[本文引用: 3]
FU S Y, LYU T L, MIN F Q, et al. Review of estimation methods on SOC of lithium-ion batteries in electric vehicles[J]. Energy Storage Science and Technology, 2021, 10(3): 1127-1136.
[本文引用: 3]
[5]
苏航, 高怀斌, 李争光, 等. 基于BCRLS-ACKF的锂离子电池荷电状态估计[J]. 储能科学与技术, 2021, 10(6): 2334-2341.
[本文引用: 1]
SU H, GAO H B, LI Z G, et al. State of charge estimation of Li-ion battery based on BCRLS-ACKF[J]. Energy Storage Science and Technology, 2021, 10(6): 2334-2341.
[本文引用: 1]
[6]
封居强, 伍龙, 黄凯峰, 等. 基于FFRLS和AEKF的锂离子电池SOC在线估计研究[J]. 储能科学与技术, 2021, 10(1): 242-249.
[本文引用: 1]
FENG J Q, WU L, HUANG K F, et al. Online SOC estimation of a lithium-ion battery based on FFRLS and AEKF[J]. Energy Storage Science and Technology, 2021, 10(1): 242-249.
[本文引用: 1]
[7]
陈峥, 赵广达, 沈世全, 等. 基于迁移模型的老化锂离子电池SOC估计[J]. 储能科学与技术, 2021, 10(1): 326-334.
[本文引用: 1]
CHEN Z, ZHAO G D, SHEN S Q, et al. SOC estimation of aging lithium-ion battery based on a migration model[J]. Energy Storage Science and Technology, 2021, 10(1): 326-334.
[本文引用: 1]
[8]
李骏, 魏炜阳, 刘霏霏, 等. 基于噪声模型的锂离子电池SOC预测[J]. 电池, 2020, 50(3): 249-253.
[本文引用: 1]
LI J, WEI W Y, LIU F F, et al. SOC prediction for Li-ion battery based on noise model[J]. Battery Bimonthly, 2020, 50(3): 249-253.
[本文引用: 1]
[9]
刘长贺,胡明辉,李兰.基于温变双极化模型的锂离子电池荷电状态估计[J/OL].重庆大学学报.[2022-01-15]. http://qks.cqu.edu.cn/cqdxzrcn/article/abstract/zk-202106056
[本文引用: 1]
LIU C H, HU M H, LI L. State of charge estimation of Li-ion battery based on temperature-variable dual polarization model[J/OL]. Journal of Chongqing University.[2022-01-15]. http://qks.cqu.edu.cn/cqdxzrcn/article/abstract/zk-202106056
[本文引用: 1]
[10]
潘凤文, 弓栋梁, 高莹, 等. 基于鲁棒H∞ 滤波的锂离子电池SOC估计[J]. 工程科学学报, 2021, 43(5): 693-701.
[本文引用: 2]
PAN F W, GONG D L, GAO Y, et al. Lithium-ion battery state of charge estimation based on a robust H∞ filter[J]. Chinese Journal of Engineering, 2021, 43(5): 693-701.
[本文引用: 2]
[11]
刘晓悦, 魏宇册. 优化神经网络的锂电池SOC估算[J]. 机械设计与制造, 2021(11): 83-86.
[本文引用: 1]
LIU X Y, WEI Y C. Optimization of neural network for lithium nattery SOC estimation[J]. Machinery Design & Manufacture, 2021(11): 83-86.
[本文引用: 1]
[12]
陆佳伟, 佘世刚, 魏新尧, 等. 基于布谷鸟搜索优化神经网络的锂电池荷电状态预测[J]. 计算机测量与控制, 2021, 29(8): 47-50, 88.
[本文引用: 1]
LU J W, SHE S G, WEI X Y, et al. Lithium battery charge status prediction based on cuckoo search optimization neural networks[J]. Computer Measurement & Control, 2021, 29(8): 47-50, 88.
[本文引用: 1]
[13]
王语园, 李嘉波, 张福. 基于粒子群算法的最小二乘支持向量机电池状态估计[J]. 储能科学与技术, 2020, 9(4): 1153-1158.
[本文引用: 2]
WANG Y Y, LI J B, ZHANG F. Battery state estimation of least squares support vector machinebased on particle swarm optimization[J]. Energy Storage Science and Technology, 2020, 9(4): 1153-1158.
[本文引用: 2]
[14]
鲍伟, 葛建军. 基于稀疏采样数据的电动公交车电池SOC预测方法研究[J]. 汽车工程, 2020, 42(3): 367-374.
[本文引用: 1]
BAO W, GE J J. Study on battery SOC prediction method for ElectricBus based on sparsely sampled data[J]. Automotive Engineering, 2020, 42(3): 367-374.
[本文引用: 1]
[15]
田冬冬, 李立伟, 杨玉新. 基于改进BP-EKF算法的SOC估算[J]. 电源技术, 2020, 44(9): 1274-1278.
[本文引用: 1]
TIAN D D, LI L W, YANG Y X. Research on SOC estimation based on improved BP-EKF algorithm[J]. Chinese Journal of Power Sources, 2020, 44(9): 1274-1278.
[本文引用: 1]
[16]
张远进, 吴华伟, 叶从进. 基于AUKF-BP神经网络的锂电池SOC估算[J]. 储能科学与技术, 2021, 10(1): 237-241.
[本文引用: 1]
ZHANG Y J, WU H W, YE C J. Estimation of the SOC of a battery based on the AUKF-BP algorithm[J]. Energy Storage Science and Technology, 2021, 10(1): 237-241.
[本文引用: 1]
[17]
张照娓, 郭天滋, 高明裕, 等. 电动汽车锂离子电池荷电状态估算方法研究综述[J]. 电子与信息学报, 2021, 43(7): 1803-1815.
[本文引用: 1]
ZHANG Z W, GUO T Z, GAO M Y, et al. Review of SOC estimation methods for electric vehicle Li-ion batteries[J]. Journal of Electronics & Information Technology, 2021, 43(7): 1803-1815.
[本文引用: 1]
[18]
国家市场监督管理总局, 国家标准化管理委员会. 电力系统电化学储能系统通用技术条件: GB/T 36558—2018[S]. 北京: 中国标准出版社, 2018.
[本文引用: 1]
[19]
国家市场监督管理总局, 国家标准化管理委员会. 电动汽车用电池管理系统技术条件: GB/T 38661—2020[S]. 北京: 中国标准出版社, 2020.
[本文引用: 1]
[20]
国家质量监督检验检疫总局, 中国国家标准化管理委员会. 电化学储能电站用锂离子电池管理系统技术规范: GB/T 34131—2017[S]. 北京: 中国标准出版社, 2017.
[本文引用: 1]
[21]
韦振汉. 锂离子电池荷电及健康状态预测方法研究[D].广西师范大学,2018.
[本文引用: 2]
WEI Z H. Research on methods for lithium ion battery SOC estimation and soh prediction[D]. Guilin: Guangxi Normal University, 2018.
[本文引用: 2]
[22]
续远.基于安时积分法与开路电压法估测电池SOC[J].新型工业化,2022,12(01):123-124+127.
[本文引用: 2]
XU Y.Estimation of battery SOC based on ampere-hour integration method and open circuit voltage method[J].The Journal of New Industrialization,2022,12(01):123-124+127.
[本文引用: 2]
[23]
郑欣昊. 海洋浮标能量收集器电源管理系统的设计与实现[D]. 哈尔滨: 哈尔滨工业大学, 2019.
[本文引用: 4]
ZHENG X H. Design and implementation of power management system for ocean buoy energy collector[D]. Harbin: Harbin Institute of Technology, 2019.
[本文引用: 4]
[24]
许洁茹, 凌仕刚, 王少飞, 等. 锂电池研究中的电导率测试分析方法[J]. 储能科学与技术, 2018, 7(5): 926-955.
[本文引用: 2]
XU J R, LING S G, WANG S F, et al. Conductivity test and analysis methods for research of lithium batteries[J]. Energy Storage Science and Technology, 2018, 7(5): 926-955.
[本文引用: 2]
[25]
李建林, 屈树慷, 黄孟阳, 等. 锂离子电池建模现状研究综述[J]. 热力发电, 2021, 50(7): 1-7.
[本文引用: 1]
LI J L, QU S K, HUANG M Y, et al. A review of current research on lithium-ion battery modeling[J]. Thermal Power Generation, 2021, 50(7): 1-7.
[本文引用: 1]
[26]
李涛, 程夕明, 胡晨华. 锂离子电池电化学降阶模型性能对比[J]. 物理学报, 2021, 70(13): 429-440.
[本文引用: 1]
LI T, CHENG X M, HU C H. Comparative study of reduced-order electrochemical models of the lithium-ion battery[J]. Acta Physica Sinica, 2021, 70(13): 429-440.
[本文引用: 1]
[27]
李雄, 李英豪, 李晨阳, 等. 基于温度和SOC的退役电池电化学阻抗特性[J]. 电池, 2021, 51(2): 126-130.
[本文引用: 1]
LI X, LI Y H, LI C Y, et al. Electrochemical impedance characteristics of retired battery based on temperature and SOC[J]. Battery Bimonthly, 2021, 51(2): 126-130.
[本文引用: 1]
[28]
李建林, 肖珩. 锂离子电池建模现状综述[J]. 储能科学与技术, 2022, 11(2): 697-703.
[本文引用: 1]
LI J L, XIAO H. Review on modeling of lithium-ion battery[J]. Energy Storage Science and Technology, 2022, 11(2): 697-703.
[本文引用: 1]
[29]
杨杰, 王婷, 杜春雨, 等. 锂离子电池模型研究综述[J]. 储能科学与技术, 2019, 8(1): 58-64.
[本文引用: 1]
YANG J, WANG T, DU C Y, et al. Overview of the modeling of lithium-ion batteries[J]. Energy Storage Science and Technology, 2019, 8(1): 58-64.
[本文引用: 1]
[30]
吴小慧, 张兴敢. 锂电池二阶RC等效电路模型参数辨识[J]. 南京大学学报(自然科学), 2020, 56(5): 754-761.
[本文引用: 1]
WU X H, ZHANG X G. Parameters identification of second order RC equivalent circuit model for lithium batteries[J]. Journal of Nanjing University (Natural Science), 2020, 56(5): 754-761.
[本文引用: 1]
[31]
李建林, 梁忠豪, 李雅欣, 等. 锂电池储能系统建模发展现状及其数据驱动建模初步探讨[J]. 油气与新能源, 2021, 33(4): 75-81.
[本文引用: 1]
LI J L, LIANG Z H, LI Y X, et al. Development status in modeling of the lithium battery energy storage system and preliminary exploration of its data-driven modeling[J]. Petroleum and New Energy, 2021, 33(4): 75-81.
[本文引用: 1]
[32]
张少凤, 张清勇, 杨叶森, 等. 基于滑动窗口和LSTM神经网络的锂离子电池建模方法[J]. 储能科学与技术, 2022, 11(1): 228-239.
[本文引用: 1]
ZHANG S F, ZHANG Q Y, YANG Y S, et al. Lithium-ion battery model based on sliding window and long short term memory neural network[J]. Energy Storage Science and Technology, 2022, 11(1): 228-239.
[本文引用: 1]
[33]
吕力行, 刘骅, 徐雷, 等. 基于数据-模型混合驱动的锂电池储能系统状态估计及预警方法[J]. 热力发电, 2021, 50(8): 64-72.
[本文引用: 1]
LYU L X, LIU H, XU L, et al. State estimation and early warning method for lithium battery energy storage system based on data-model hybrid drive[J]. Thermal Power Generation, 2021, 50(8): 64-72.
[本文引用: 1]
[34]
代明杰, 张磊, 江学焕. 基于二阶Thevenin模型的卡尔曼滤波SOC估计[J]. 湖北汽车工业学院学报, 2021, 35(4): 55-58.
[本文引用: 1]
DAI M J, ZHANG L, JIANG X H. Kalman filter SOC estimation based on second order thevenin model[J]. Journal of Hubei University of Automotive Technology, 2021, 35(4): 55-58.
[本文引用: 1]
[35]
郝文美, 张立伟, 彭博, 等. 动车组钛酸锂电池荷电状态估计[J]. 电工技术学报, 2021, 36(S1): 362-371.
[本文引用: 2]
HAO W M, ZHANG L W, PENG B, et al. State of charge estimation of lithium titanate battery for electric multiple units[J]. Transactions of China Electrotechnical Society, 2021, 36(S1): 362-371.
[本文引用: 2]
[36]
曹天佳,李欢欢,韩军,等. 基于扩展卡尔曼滤波的锂电池SOC估计算法[C]//2021中国汽车工程学会年会论文集(2),2021:187-193.
[本文引用: 2]
CAO T J, LI H H, HAN J, et al. Lithium battery SOC estimation algorithm based on extended Kalman filter[C]//Proceedings of the 2021 China Society of Automotive Engineers Annual Conference (2), 2021:187-193.
[本文引用: 2]
[37]
田曜荣, 宋春宁, 莫伟县. 基于无迹卡尔曼滤波单液流锌镍电池SOC估计[J]. 计算机仿真, 2021, 38(11): 73-76, 81.
[本文引用: 1]
TIAN Y R, SONG C N, MO W X. SOC estimation of single flow zinc nickel battery based on unscented Kalman filter[J]. Computer Simulation, 2021, 38(11): 73-76, 81.
[本文引用: 1]
[38]
杨淇, 孙桓五, 张凤博. 锂电SOC改进无迹卡尔曼滤波估算算法研究[J]. 机械设计与制造, 2021(10): 220-224.
[本文引用: 1]
YANG Q, SUN H W, ZHANG F B. Research on SOC improved unscented Kalman filter estimation algorithm for lithium batteries[J]. Machinery Design & Manufacture, 2021(10): 220-224.
[本文引用: 1]
[39]
LUO J Y, PENG J K, HE H W. Lithium-ion battery SOC estimation study based on Cubature Kalman filter[J]. Energy Procedia, 2019, 158: 3421-3426.
[本文引用: 1]
[40]
宋琴, 王顺利, 于春梅. 自适应卡尔曼对储能锂电池充放电状态的估算[J]. 自动化仪表, 2021, 42(5): 63-68.
[本文引用: 1]
SONG Q, WANG S L, YU C M. Estimation of charge and discharge state of energy storage lithium battery by adaptive Kalman[J]. Process Automation Instrumentation, 2021, 42(5): 63-68.
[本文引用: 1]
[41]
黄鹏超, 鄂加强. 基于双自适应卡尔曼滤波的锂电池状态估算[J]. 储能科学与技术, 2022, 11(2): 660-666.
HUANG P C, E J Q. State estimation of lithium-ion battery based on dual adaptive Kalman filter[J]. Energy Storage Science and Technology, 2022, 11(2): 660-666.
[42]
王志福, 李仁杰, 李霞. 基于混合AUKF和HIFF的锂离子电池SOC估计[J]. 电池, 2021, 51(4): 380-384.
[本文引用: 2]
WANG Z F, LI R J, LI X. SOC estimation of Li-ion battery based on mixed AUKF and HIFF[J]. Battery Bimonthly, 2021, 51(4): 380-384.
[本文引用: 2]
[43]
杨朝红, 马彬, 黄明浩, 等. 基于OCV分段拟合的电池SOC估计方法研究[J]. 计算机仿真, 2021, 38(11): 82-88, 157.
[本文引用: 1]
YANG Z H, MA B, HUANG M H, et al. Research on state of charge estimation method of lithium battery based on open-circuit voltage piecewise fitting[J]. Computer Simulation, 2021, 38(11): 82-88, 157.
[本文引用: 1]
[44]
李练兵, 孙坤, 季亮, 等. 基于双卡尔曼滤波的电池SOC估算[J]. 计算机工程与设计, 2021, 42(11): 3218-3224.
[本文引用: 1]
LI L B, SUN K, JI L, et al. Battery SOC estimation based on double Kalman filter[J]. Computer Engineering and Design, 2021, 42(11): 3218-3224.
[本文引用: 1]
[45]
刘习奎. 基于双扩展卡尔曼滤波的锂电池荷电状态估算方法[J]. 电子制作, 2021(21): 93-95.
[本文引用: 1]
LIU X K. Estimation method of lithium battery state of charge based on double extended Kalman filter[J]. Practical Electronics, 2021(21): 93-95.
[本文引用: 1]
[46]
陈剑, 肖振锋, 刘顺成, 等. 基于EKF-SVSF的锂离子电池SOC和SOH准确估计[J]. 电源技术, 2020, 44(10): 1483-1487.
[本文引用: 1]
CHEN J, XIAO Z F, LIU S C, et al. Accurate estimation of SOC and SOH of Li-ion battery based on EKF-SVSF[J]. Chinese Journal of Power Sources, 2020, 44(10): 1483-1487.
[本文引用: 1]
[47]
朱磊, 刘子博, 李路路, 等. 基于RLS-DLUKF算法的锂电池SOC预测方法研究[J]. 储能科学与技术, 2021, 10(3): 1137-1144.
[本文引用: 1]
ZHU L, LIU Z B, LI L L, et al. Research on a battery SOC prediction method based on the RLS-DLUKF algorithm[J]. Energy Storage Science and Technology, 2021, 10(3): 1137-1144.
[本文引用: 1]
[48]
朱奕楠, 吕桃林, 赵芝芸, 等. 基于并行卡尔曼滤波器的锂离子电池荷电状态估计[J]. 储能科学与技术, 2021, 10(6): 2352-2362.
[本文引用: 1]
ZHU Y N, LÜ T L, ZHAO Z Y, et al. State of charge estimation of lithium ion battery based on parallel Kalman filter[J]. Energy Storage Science and Technology, 2021, 10(6): 2352-2362.
[本文引用: 1]
[49]
单成鑫, 李立伟, 杨玉新. 基于IACO-PF的锂电池SOC估算[J]. 储能科学与技术, 2021, 10(3): 1145-1152.
[本文引用: 1]
SHAN C X, LI L W, YANG Y X. SOC of estimation of lithium battery based on IACO-PF[J]. Energy Storage Science and Technology, 2021, 10(3): 1145-1152.
[本文引用: 1]
[50]
刘淑杰, 郝昆昆, 王永, 等. 基于改进粒子滤波算法的动力锂离子电池荷电状态估计[J]. 大连理工大学学报, 2020, 60(4): 392-401.
[本文引用: 2]
LIU S J, HAO K K, WANG Y, et al. State of charge estimation of power lithium-ion battery based on improved particle filter algorithms[J]. Journal of Dalian University of Technology, 2020, 60(4): 392-401.
[本文引用: 2]
[51]
彭方想, 南金瑞, 孙立清. 基于权值选择粒子滤波算法的锂离子电池SOC估计[J]. 太原理工大学学报, 2020, 51(5): 750-755.
[本文引用: 1]
PENG F X, NAN J R, SUN L Q. SOC estimation of lithium-ion battery based on weight selection particle filter algorithm[J]. Journal of Taiyuan University of Technology, 2020, 51(5): 750-755.
[本文引用: 1]
[52]
袁建华, 刘雅萍, 赵子玮, 等. 基于IGWO-PF算法的无人机锂电池SOC估计[J]. 储能科学与技术, 2022, 11(5): 1601-1607.
[本文引用: 2]
YUAN J H, LIU Y P, ZHAO Z W, et al. SOC estimation of UAV lithium battery based on IGWO-PF algorithm[J]. Energy Storage Science and Technology, 2022, 11(5): 1601-1607.
[本文引用: 2]
[53]
熊巍, 梅华平, 徐刚, 等. 基于改进H无穷滤波的锂离子电池SOC估计[J]. 电源技术, 2020, 44(10): 1488-1491, 1528.
[本文引用: 2]
XIONG W, MEI H P, XU G, et al. Lithium-ion battery SOC estimation based on improved H-infinity filter[J]. Chinese Journal of Power Sources, 2020, 44(10): 1488-1491, 1528.
[本文引用: 2]
[54]
YU Q Q, XIONG R, YANG R X, et al. Online capacity estimation for lithium-ion batteries through joint estimation method[J]. Applied Energy, 2019, 255:doi: 10.1016/j.apenergy.2019.113817.
[本文引用: 2]
[55]
丁洁, 姚建鑫, 万佑红, 等. 基于加权多新息H∞ 滤波的锂离子电池SOC估计[J]. 电池, 2020, 50(5): 432-435.
[本文引用: 1]
DING J, YAO J X, WAN Y H, et al. SOC estimation for Li-ion battery based on weighted innovation H∞ filter[J]. Battery Bimonthly, 2020, 50(5): 432-435.
[本文引用: 1]
[56]
于仲安, 卢健, 王先敏. 基于GA-BP神经网络的锂离子电池SOC估计[J]. 电源技术, 2020, 44(3): 337-340, 421.
[本文引用: 2]
YU Z A, LU J, WANG X M. SOC estimation of Li-ion battery based on GA-BP neural network[J]. Chinese Journal of Power Sources, 2020, 44(3): 337-340, 421.
[本文引用: 2]
[57]
王桥, 魏孟, 叶敏, 等. 基于灰狼算法优化极限学习机的锂离子电池SOC估计[J]. 储能科学与技术, 2021, 10(2): 744-751.
[本文引用: 2]
WANG Q, WEI M, YE M, et al. Estimation of lithium-ion battery SOC based on GWO-optimized extreme learning machine[J]. Energy Storage Science and Technology, 2021, 10(2): 744-751.
[本文引用: 2]
[58]
赵超, 王延峰, 林立. 基于改进灰狼算法优化核极限学习机的锂电池动力电池荷电状态估计[J]. 信息与控制, 2021, 50(6): 731-739.
[本文引用: 1]
ZHAO C, WANG Y F, LIN L. State of charge estimation for lithium battery based on kernel extreme learning machine optimized by improved grey wolf algorithm[J]. Information and Control, 2021, 50(6): 731-739.
[本文引用: 1]
[59]
王帅, 马鸿雁, 窦嘉铭, 等. 基于UGOA-BP的锂电池SOC估算[J]. 储能科学与技术, 2022, 11(1): 258-264.
[本文引用: 1]
WANG S, MA H Y, DOU J M, et al. Estimation of lithium-ion battery state of charge based on UGOA-BP[J]. Energy Storage Science and Technology, 2022, 11(1): 258-264.
[本文引用: 1]
[60]
张小辉, 许傲然, 王秀平. 回溯搜索算法改进RBF算法的锂离子电池SOC估算研究[J]. 电测与仪表, 2020, 57(18): 146-152.
[本文引用: 2]
ZHANG X H, XU A R, WANG X P. Research on lithium-ion battery SOC estimation based on backtracking search algorithm and improved RBF algorithm[J]. Electrical Measurement & Instrumentation, 2020, 57(18): 146-152.
[本文引用: 2]
[61]
陈德海, 丁博文, 潘韦驰. 基于LFOA-GRNN模型的矿用锂电池SOC预测[J]. 现代电子技术, 2020, 43(6): 115-118.
[本文引用: 2]
CHEN D H, DING B W, PAN W C. Mining lithium battery SOC prediction based on LFOA-GRNN model[J]. Modern Electronics Technique, 2020, 43(6): 115-118.
[本文引用: 2]
[62]
钱建文, 杜翀, 田欣, 等. 一种改进T-S模糊神经网络估计锂电池SOC的方法[J]. 电源技术, 2020, 44(9): 1270-1273.
[本文引用: 2]
QIAN J W, DU C, TIAN X, et al. An improved fuzzy neural network method based on T-S model to estimate state of charge of lithium batteries[J]. Chinese Journal of Power Sources, 2020, 44(9): 1270-1273.
[本文引用: 2]
[63]
曹新宇, 彭飞, 李立伟, 等. 基于IBAS-NARX神经网络的锂电池荷电状态估计[J]. 储能科学与技术, 2021, 10(6): 2342-2351.
[本文引用: 2]
CAO X Y, PENG F, LI L W, et al. SOC estimation of lithium battery based on IBAS-NARX neural network model[J]. Energy Storage Science and Technology, 2021, 10(6): 2342-2351.
[本文引用: 2]
[64]
明彤彤, 赵晶, 王晓磊, 等. 基于改进LSTM的脉冲大倍率工况下锂电池SOC估计[J]. 电力系统保护与控制, 2021, 49(8): 144-150.
[本文引用: 2]
MING T T, ZHAO J, WANG X L, et al. SOC estimation of a lithium battery under high pulse rate condition based on improved LSTM[J]. Power System Protection and Control, 2021, 49(8): 144-150.
[本文引用: 2]
[65]
朱元富, 贺文武, 李建兴, 等. 基于Bi-LSTM/Bi-GRU循环神经网络的锂电池SOC估计[J]. 储能科学与技术, 2021, 10(3): 1163-1176.
[本文引用: 2]
ZHU Y F, HE W W, LI J X, et al. SOC estimation for Li-ion batteries based on Bi-LSTM and Bi-GRU[J]. Energy Storage Science and Technology, 2021, 10(3): 1163-1176.
[本文引用: 2]
[66]
李超然, 肖飞, 樊亚翔, 等. 基于门控循环单元神经网络和Huber-M估计鲁棒卡尔曼滤波融合方法的锂离子电池荷电状态估算方法[J]. 电工技术学报, 2020, 35(9): 2051-2062.
[本文引用: 1]
LI C R, XIAO F, FAN Y X, et al. A hybrid approach to lithium-ion battery SOC estimation based on recurrent neural network with gated recurrent unit and Huber-M robust Kalman filter[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 2051-2062.
[本文引用: 1]
[67]
王仲旭, 张圣渠, 刘强. 基于GA和PSO的电动客车锂离子电池SOC估计[J]. 电池, 2021, 51(3): 221-224.
[本文引用: 2]
WANG Z X, ZHANG S Q, LIU Q. SOC estimation of Li-ion battery in electric bus based on GA and PSO[J]. Battery Bimonthly, 2021, 51(3): 221-224.
[本文引用: 2]
[68]
成文晶, 潘庭龙. 基于分布估计算法LSSVM的锂电池SOC预测[J]. 储能科学与技术, 2020, 9(6): 1948-1953.
[本文引用: 1]
CHENG W J, PAN T L. Prediction for SOC of lithium-ion batteries by estimating the distribution algorithm with LSSVM[J]. Energy Storage Science and Technology, 2020, 9(6): 1948-1953.
[本文引用: 1]
[69]
舒星,刘永刚,申江卫,陈峥.基于改进最小二乘支持向量机与Box-Cox变换的锂离子电池容量预测[J].机械工程学报,2021,57(14):118-128.
[本文引用: 2]
SHU X, LIU Y G, SHEN J W, et al.Capacity prediction of lithium-ion batteries based on improved least squares support vector machine and Box-Cox transform[J].Chinese Journal of Mechanical Engineering,2021,57(14):118-128.
[本文引用: 2]
[70]
李超然, 肖飞, 樊亚翔, 等. 基于高斯过程回归的锂电池SOC估算方法[J]. 海军工程大学学报, 2021, 33(1): 55-59.
[本文引用: 2]
LI C R, XIAO F, FAN Y X, et al. State of charge estimation method for lithium battery based on Gaussian process regression[J]. Journal of Naval University of Engineering, 2021, 33(1): 55-59.
[本文引用: 2]
[71]
魏孟, 李嘉波, 叶敏, 等. 基于高斯混合回归的锂离子电池SOC估计[J]. 储能科学与技术, 2020, 9(3): 958-963.
[本文引用: 1]
WEI M, LI J B, YE M, et al. SOC estimation of Li-ion battery based on Gaussian mixture regression[J]. Energy Storage Science and Technology, 2020, 9(3): 958-963.
[本文引用: 1]
[72]
孙爱芬, 赤娜. 基于改进的高斯过程回归的SOC估计算法[J]. 储能科学与技术, 2022, 11(1): 253-257.
SUN A F, CHI N. SOC estimation algorithm based on improved Gaussian process regression[J]. Energy Storage Science and Technology, 2022, 11(1): 253-257.
[73]
马向平, 靳皓晴, 朱奇先, 等. 锂离子电池荷电状态的在线融合估计方法[J]. 兰州理工大学学报, 2020, 46(5): 78-84.
[本文引用: 3]
MA X P, JIN H Q, ZHU Q X, et al. An online fusion estimation method for state of charge of lithium ion batteries[J]. Journal of Lanzhou University of Technology, 2020, 46(5): 78-84.
[本文引用: 3]
[74]
刘兴涛, 李坤, 武骥, 等. 基于EKF-SVM算法的动力电池SOC估计[J]. 汽车工程, 2020, 42(11): 1522-1528, 1544.
[本文引用: 2]
LIU X T, LI K, WU J, et al. State of charge estimation for traction battery based on EKF-SVM algorithm[J]. Automotive Engineering, 2020, 42(11): 1522-1528, 1544.
[本文引用: 2]
[75]
丁羿茗, 吕瑞强, 蒋超. 基于EKF算法的神经网络估算锂电池SOC[J]. 电源技术, 2021, 45(10): 1260-1263.
[本文引用: 2]
DING Y M, LV R Q, JIANG C. Estimation of lithium battery SOC based on EKF neural network[J]. Chinese Journal of Power Sources, 2021, 45(10): 1260-1263.
[本文引用: 2]
[76]
辛浩东, 赵欣, 周昊, 等. 基于LSTM-UKF的全电船用锂电池SOC容量估计[J]. 船舶工程, 2021, 43(11): 111-117.
[本文引用: 2]
XIN H D, ZHAO X, ZHOU H, et al. SOC capacity estimation method of lithium-ion batteries in all-electric ships based on LSTM-UKF[J]. Ship Engineering, 2021, 43(11): 111-117.
[本文引用: 2]
[77]
寇发荣, 王思俊, 王甜甜, 等. VCM模型下的IBAS-EKF锂电池荷电状态估计[J]. 机械科学与技术, 2021, 40(12): 1929-1938.
[本文引用: 1]
KOU F R, WANG S J, WANG T T, et al. IBAS-EKF estimation of lithium battery state of charge under VCM[J]. Mechanical Science and Technology for Aerospace Engineering, 2021, 40(12): 1929-1938.
[本文引用: 1]
[78]
李军, 张俊, 张世义. 基于ABP-EKF算法的锂电池SOC估计[J]. 重庆交通大学学报(自然科学版), 2021, 40(3): 135-140.
[本文引用: 1]
LI J, ZHANG J, ZHANG S Y. Lithium battery SOC estimation based on ABP-EKF algorithm[J]. Journal of Chongqing Jiaotong University (Natural Science), 2021, 40(3): 135-140.
[本文引用: 1]
[79]
张吉昂, 王萍, 程泽. 基于充电电压片段和融合方法的锂离子电池SOC-SOH-RUL联合估计[J]. 电网技术, 2022, 46(3): 1063-1072.
[本文引用: 1]
ZHANG J, WANG P, CHENG Z. A joint estimation framework of SOC-SOH-RUL for lithium batteries based on charging voltage segment and hybrid method[J]. Power System Technology, 2022, 46(3): 1063-1072.
[本文引用: 1]
[80]
李名莉, 邱兵涛, 贾琳鹏. 锂电池组剩余电量SOC估算方法的分析与研究[J]. 自动化仪表, 2019, 40(4): 56-59.
[本文引用: 1]
LI M L, QIU B T, JIA L P. Analysis and research on SOC estimation method for residual power of lithium battery packs[J]. Process Automation Instrumentation, 2019, 40(4): 56-59.
[本文引用: 1]
[81]
贾海峰, 李聪. 基于BP神经网络的锂电池组SOC估算[J]. 农业装备与车辆工程, 2020, 58(1): 105-107, 112.
[本文引用: 1]
JIA H F, LI C. SOC estimation of lithium battery pack based on BP neural network[J]. Agricultural Equipment & Vehicle Engineering, 2020, 58(1): 105-107, 112.
[本文引用: 1]
[82]
何锋, 王文亮, 蒋雪生, 等. 双扩展卡尔曼滤波法估计锂电池组SOC与SOH[J]. 农业装备与车辆工程, 2021, 59(7): 37-40, 61.
[本文引用: 1]
HE F, WANG W L, JIANG X S, et al. Estimation of SOC and SOH of lithium battery pack by double extended Kalman filter[J]. Agricultural Equipment & Vehicle Engineering, 2021, 59(7): 37-40, 61.
[本文引用: 1]
1
... 锂电池具有能量密度大、效率高、循环寿命长、自放电率低等优点,被广泛应用于电力储能和电动汽车之中[1 ] .据不完全统计[2 ] ,截止到2020年底,我国锂离子电池投运装机规模累计2902.4 MW,占电化学储能的88.8%,呈现为最主要的电化学储能类型.而高精度、快速实时的锂电池荷电状态(state of charge)估计技术是保障锂电池运行安全、可靠性以及延长使用寿命的核心技术,对锂电池更大规模的应用具有重要工程价值. ...
1
... 锂电池具有能量密度大、效率高、循环寿命长、自放电率低等优点,被广泛应用于电力储能和电动汽车之中[1 ] .据不完全统计[2 ] ,截止到2020年底,我国锂离子电池投运装机规模累计2902.4 MW,占电化学储能的88.8%,呈现为最主要的电化学储能类型.而高精度、快速实时的锂电池荷电状态(state of charge)估计技术是保障锂电池运行安全、可靠性以及延长使用寿命的核心技术,对锂电池更大规模的应用具有重要工程价值. ...
1
... 锂电池具有能量密度大、效率高、循环寿命长、自放电率低等优点,被广泛应用于电力储能和电动汽车之中[1 ] .据不完全统计[2 ] ,截止到2020年底,我国锂离子电池投运装机规模累计2902.4 MW,占电化学储能的88.8%,呈现为最主要的电化学储能类型.而高精度、快速实时的锂电池荷电状态(state of charge)估计技术是保障锂电池运行安全、可靠性以及延长使用寿命的核心技术,对锂电池更大规模的应用具有重要工程价值. ...
1
... 锂电池具有能量密度大、效率高、循环寿命长、自放电率低等优点,被广泛应用于电力储能和电动汽车之中[1 ] .据不完全统计[2 ] ,截止到2020年底,我国锂离子电池投运装机规模累计2902.4 MW,占电化学储能的88.8%,呈现为最主要的电化学储能类型.而高精度、快速实时的锂电池荷电状态(state of charge)估计技术是保障锂电池运行安全、可靠性以及延长使用寿命的核心技术,对锂电池更大规模的应用具有重要工程价值. ...
3
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
... 对锂电池可用容量的准确估计是对其SOC进行估计的基础,传统的SOC估计方法是通过自身参数进行估算[3 ] ,主要包括:①放电法[21 ] ,一种实验室环境下可靠的锂电池SOC估计测试方法,将锂电池以恒定电流持续放电至截止条件,将放电时间和放电电流相乘,便可得到放出的电量,进而可以计算出电池SOC值;②开路电压法[22 ] ,将锂电池进行长时间的静置,测量其开路电压和SOC,通过拟合电池开路电压与SOC的函数关系,然后通过该曲线对锂电池的SOC进行估计;③电导法[23 ] ,类似开路电压法,通过对锂电池电导值跟踪、测试,挖掘锂电池电导值与SOC之间的关系,归纳出映射规律实现对SOC估计;④交流阻抗法[24 ] ,类似于电导法,不同之处在于该方法对锂电池的阻抗进行跟踪测试;⑤安时积分法[4 ] ,是一种可用于在线检测的粗放式锂电池SOC计算方法,以电荷量是电流在时间上的积分为理论基础,在确定初始电量后对锂电池的充放电电流进行积分,再用初始电量加上或减去充放电获得或失去的电量,便可得到锂电池的实时容量,进而计算实时SOC,如公式(2) 所示.对比上述各类方法优缺点,如表3 所示. ...
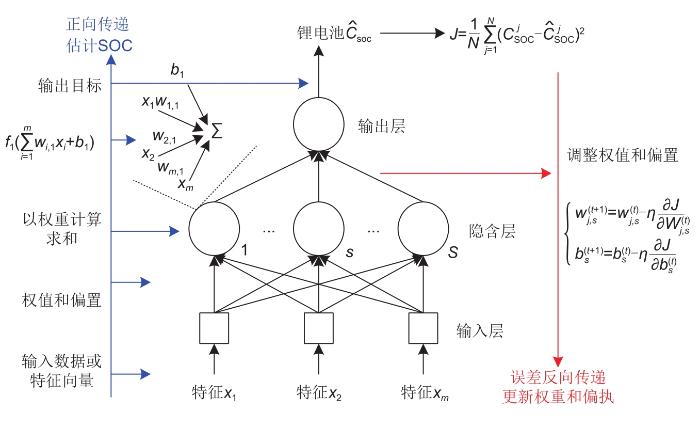
... 作为机器学习计算中最被广泛研究的回归模型,神经网络是一种由输入层、隐含层和输出层结构组成,构建输入变量至输出变量映射关系的数学网络模型.在理论上,神经网络可以通过网络层数和神经元数量的增加完成任何函数关系的拟合.在锂电池SOC估计的应用中,显而易见的是锂电池当前SOC可由前一时刻SOC、充放电电流、电池端电压、电池温度等因素决定,形成一种未知的函数关系形式.因此,可以将SOC影响因素或其二次加工的特征变量作为输入变量,SOC值作为输出变量,通过大量实际历史数据、链式导数法则以及梯度优化算法整定神经网络参数,完成由可测变量至锂电池SOC值的映射,形成估计算法[3 ] ,其结构如图6 所示. ...
3
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
... 对锂电池可用容量的准确估计是对其SOC进行估计的基础,传统的SOC估计方法是通过自身参数进行估算[3 ] ,主要包括:①放电法[21 ] ,一种实验室环境下可靠的锂电池SOC估计测试方法,将锂电池以恒定电流持续放电至截止条件,将放电时间和放电电流相乘,便可得到放出的电量,进而可以计算出电池SOC值;②开路电压法[22 ] ,将锂电池进行长时间的静置,测量其开路电压和SOC,通过拟合电池开路电压与SOC的函数关系,然后通过该曲线对锂电池的SOC进行估计;③电导法[23 ] ,类似开路电压法,通过对锂电池电导值跟踪、测试,挖掘锂电池电导值与SOC之间的关系,归纳出映射规律实现对SOC估计;④交流阻抗法[24 ] ,类似于电导法,不同之处在于该方法对锂电池的阻抗进行跟踪测试;⑤安时积分法[4 ] ,是一种可用于在线检测的粗放式锂电池SOC计算方法,以电荷量是电流在时间上的积分为理论基础,在确定初始电量后对锂电池的充放电电流进行积分,再用初始电量加上或减去充放电获得或失去的电量,便可得到锂电池的实时容量,进而计算实时SOC,如公式(2) 所示.对比上述各类方法优缺点,如表3 所示. ...
... 作为机器学习计算中最被广泛研究的回归模型,神经网络是一种由输入层、隐含层和输出层结构组成,构建输入变量至输出变量映射关系的数学网络模型.在理论上,神经网络可以通过网络层数和神经元数量的增加完成任何函数关系的拟合.在锂电池SOC估计的应用中,显而易见的是锂电池当前SOC可由前一时刻SOC、充放电电流、电池端电压、电池温度等因素决定,形成一种未知的函数关系形式.因此,可以将SOC影响因素或其二次加工的特征变量作为输入变量,SOC值作为输出变量,通过大量实际历史数据、链式导数法则以及梯度优化算法整定神经网络参数,完成由可测变量至锂电池SOC值的映射,形成估计算法[3 ] ,其结构如图6 所示. ...
3
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
... 对锂电池可用容量的准确估计是对其SOC进行估计的基础,传统的SOC估计方法是通过自身参数进行估算[3 ] ,主要包括:①放电法[21 ] ,一种实验室环境下可靠的锂电池SOC估计测试方法,将锂电池以恒定电流持续放电至截止条件,将放电时间和放电电流相乘,便可得到放出的电量,进而可以计算出电池SOC值;②开路电压法[22 ] ,将锂电池进行长时间的静置,测量其开路电压和SOC,通过拟合电池开路电压与SOC的函数关系,然后通过该曲线对锂电池的SOC进行估计;③电导法[23 ] ,类似开路电压法,通过对锂电池电导值跟踪、测试,挖掘锂电池电导值与SOC之间的关系,归纳出映射规律实现对SOC估计;④交流阻抗法[24 ] ,类似于电导法,不同之处在于该方法对锂电池的阻抗进行跟踪测试;⑤安时积分法[4 ] ,是一种可用于在线检测的粗放式锂电池SOC计算方法,以电荷量是电流在时间上的积分为理论基础,在确定初始电量后对锂电池的充放电电流进行积分,再用初始电量加上或减去充放电获得或失去的电量,便可得到锂电池的实时容量,进而计算实时SOC,如公式(2) 所示.对比上述各类方法优缺点,如表3 所示. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
3
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
... 对锂电池可用容量的准确估计是对其SOC进行估计的基础,传统的SOC估计方法是通过自身参数进行估算[3 ] ,主要包括:①放电法[21 ] ,一种实验室环境下可靠的锂电池SOC估计测试方法,将锂电池以恒定电流持续放电至截止条件,将放电时间和放电电流相乘,便可得到放出的电量,进而可以计算出电池SOC值;②开路电压法[22 ] ,将锂电池进行长时间的静置,测量其开路电压和SOC,通过拟合电池开路电压与SOC的函数关系,然后通过该曲线对锂电池的SOC进行估计;③电导法[23 ] ,类似开路电压法,通过对锂电池电导值跟踪、测试,挖掘锂电池电导值与SOC之间的关系,归纳出映射规律实现对SOC估计;④交流阻抗法[24 ] ,类似于电导法,不同之处在于该方法对锂电池的阻抗进行跟踪测试;⑤安时积分法[4 ] ,是一种可用于在线检测的粗放式锂电池SOC计算方法,以电荷量是电流在时间上的积分为理论基础,在确定初始电量后对锂电池的充放电电流进行积分,再用初始电量加上或减去充放电获得或失去的电量,便可得到锂电池的实时容量,进而计算实时SOC,如公式(2) 所示.对比上述各类方法优缺点,如表3 所示. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
1
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
1
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
1
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
1
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
1
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
1
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
1
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
1
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
1
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
1
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
2
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
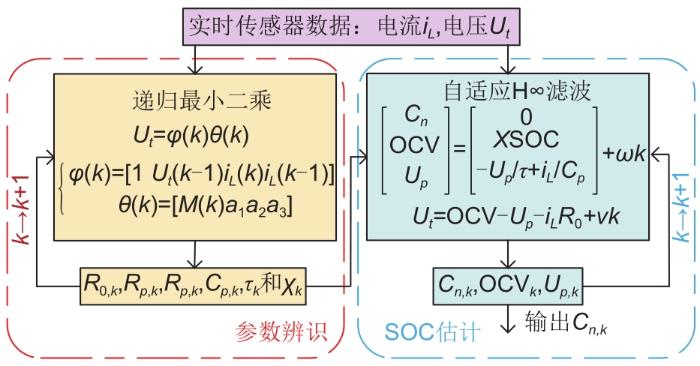
... 通过对公式(12) 的求解可以获得目标函数J <1/θ 的递推关系,获得H∞滤波器.针对传统H∞滤波对状态和模型不确定性的突变不敏感问题,文献[53 ]通过引入次优衰落因子,提高了锂电池SOC估计的稳定性;文献[10 ]将电池温度作为系统扰动变量,运用线性矩阵不等式技术设计出鲁棒H∞滤波器,较大程度地抑制了温度扰动对电池SOC估计的影响;文献[54 ]提出基于递归最小二次整定锂电池参数后,利用自适应H∞滤波进行锂电池容量估计,其实现过程如图4 所示,克服了电池SOC初始参数和测量误差对SOC估计精度的不利影响.文献[55 ]参考粒子滤波权重更迭思想,提出具有加权新息的H∞滤波算法,以时间重要性分配不同的新息权重,提高了电池SOC估计的准确性. ...
2
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
... 通过对公式(12) 的求解可以获得目标函数J <1/θ 的递推关系,获得H∞滤波器.针对传统H∞滤波对状态和模型不确定性的突变不敏感问题,文献[53 ]通过引入次优衰落因子,提高了锂电池SOC估计的稳定性;文献[10 ]将电池温度作为系统扰动变量,运用线性矩阵不等式技术设计出鲁棒H∞滤波器,较大程度地抑制了温度扰动对电池SOC估计的影响;文献[54 ]提出基于递归最小二次整定锂电池参数后,利用自适应H∞滤波进行锂电池容量估计,其实现过程如图4 所示,克服了电池SOC初始参数和测量误差对SOC估计精度的不利影响.文献[55 ]参考粒子滤波权重更迭思想,提出具有加权新息的H∞滤波算法,以时间重要性分配不同的新息权重,提高了电池SOC估计的准确性. ...
1
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
1
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
1
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
1
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
2
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
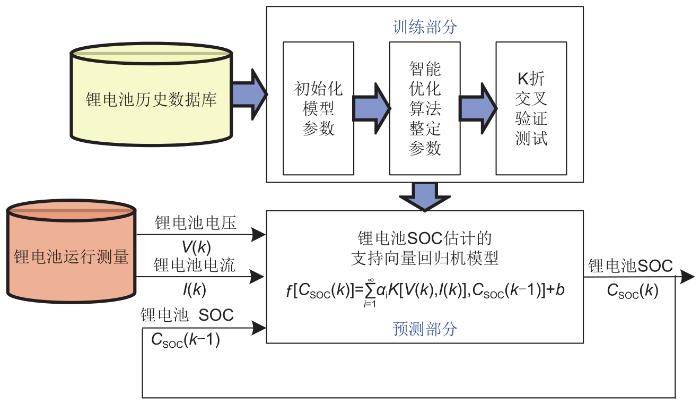
... 支持向量机是基于统计学习理论中结构风险最小化原则提出的一种机器学习算法,主要用于对数据属性分类和数据规律回归分析.其原理是通过映射低维特征空间至高维空间,实现将非线性回归问题转化为线性回归问题,通过有限数据计算出最佳模型参数,完成回归模型设计.在锂电池SOC估计应用中[13 ] ,其作用与神经网络模型一样,均是用于描述电池可测变量或二次加工特征(输入)至电池SOC(输出)的映射关系,其具体实现结构流程如图7 所示. ...
2
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
... 支持向量机是基于统计学习理论中结构风险最小化原则提出的一种机器学习算法,主要用于对数据属性分类和数据规律回归分析.其原理是通过映射低维特征空间至高维空间,实现将非线性回归问题转化为线性回归问题,通过有限数据计算出最佳模型参数,完成回归模型设计.在锂电池SOC估计应用中[13 ] ,其作用与神经网络模型一样,均是用于描述电池可测变量或二次加工特征(输入)至电池SOC(输出)的映射关系,其具体实现结构流程如图7 所示. ...
1
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
1
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
1
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
1
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
1
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
1
... 围绕锂电池SOC估计技术,国内外专家学者开展了大量研究,提出一系列锂电池SOC估计方法,获得了较好的估算性能.目前,锂电池SOC估计技术可划分为以下4类:①基于实验测试计算的传统方法[3 -4 ] ,如放电法、开路电压法、交流阻抗法等,研究人员从实验室标准条件下测试建立电池外部特性参数与SOC之间的映射关系,再通过查表或者简单计算的方式,形成对锂电池SOC的初步估算;②基于锂电池模型的滤波类方法,比较典型的算法如卡尔曼滤波及其改进型[5 -6 ] 、粒子滤波算法[7 -8 ] 以及H∞鲁棒滤波理论[9 -10 ] 等,此类方法的特色在于通过建立的锂电池数学模型更正校对安时法计算结果,以降低测量噪声和系统不确定性的影响;③基于锂电池数据驱动的机器学习类方法,开发人员引入机器学习等人工智能算法,通过挖掘大量锂电池数据下SOC的变化规律,构建锂电池特征向量至SOC的估计模型,如多种神经网络模型[11 -12 ] 和支持向量机类[13 -14 ] 的模型;④基于数模混合驱动的锂电池SOC估计方法[15 -16 ] ,开发人员通过综合锂电池模型和大数据方式,建立出模型+数据优势互补的混合估计方法,实现了对锂电池SOC估计精度的提升. ...
1
... 根据美国先进电池联合会的实验手册内容[17 ] ,SOC的定义为在一定温度下,电池放电过程中,其剩余容量和其额定容量的比值.因此,锂电池SOC的计算公式如下. ...
1
... 根据美国先进电池联合会的实验手册内容[17 ] ,SOC的定义为在一定温度下,电池放电过程中,其剩余容量和其额定容量的比值.因此,锂电池SOC的计算公式如下. ...
1
... Lithium battery usable capacity test standard
Table 2 标准编号 标准名称 SOC估计技术要求 GB/T 36558—2018[18 ] 电力系统电化学储能系统通用技术条件 能量计算误差不应大于3%,计算更新周期不应大于3 s GB/T 38661—2020[19 ] 电动汽车用电池管理系统技术条件 对于不可外接充电的混合动力电动汽车,锂电池动力电池管理系统SOC估算的累积误差应不大于15% GB/T 34131—2017[20 ] 电化学储能电站用锂离子电池管理系统技术规范 电能量计算误差应不大于3%
从表2 可以看出:①国内对电池容量测试技术较为重视,建立了多个相关国家级标准;②现有的国家标准对锂电池SOC的估算精度要求较高;③针对不同的应用场景,国家形成了不同的锂电池可容容量测试标准. ...
1
... Lithium battery usable capacity test standard
Table 2 标准编号 标准名称 SOC估计技术要求 GB/T 36558—2018[18 ] 电力系统电化学储能系统通用技术条件 能量计算误差不应大于3%,计算更新周期不应大于3 s GB/T 38661—2020[19 ] 电动汽车用电池管理系统技术条件 对于不可外接充电的混合动力电动汽车,锂电池动力电池管理系统SOC估算的累积误差应不大于15% GB/T 34131—2017[20 ] 电化学储能电站用锂离子电池管理系统技术规范 电能量计算误差应不大于3%
从表2 可以看出:①国内对电池容量测试技术较为重视,建立了多个相关国家级标准;②现有的国家标准对锂电池SOC的估算精度要求较高;③针对不同的应用场景,国家形成了不同的锂电池可容容量测试标准. ...
1
... Lithium battery usable capacity test standard
Table 2 标准编号 标准名称 SOC估计技术要求 GB/T 36558—2018[18 ] 电力系统电化学储能系统通用技术条件 能量计算误差不应大于3%,计算更新周期不应大于3 s GB/T 38661—2020[19 ] 电动汽车用电池管理系统技术条件 对于不可外接充电的混合动力电动汽车,锂电池动力电池管理系统SOC估算的累积误差应不大于15% GB/T 34131—2017[20 ] 电化学储能电站用锂离子电池管理系统技术规范 电能量计算误差应不大于3%
从表2 可以看出:①国内对电池容量测试技术较为重视,建立了多个相关国家级标准;②现有的国家标准对锂电池SOC的估算精度要求较高;③针对不同的应用场景,国家形成了不同的锂电池可容容量测试标准. ...
2
... 对锂电池可用容量的准确估计是对其SOC进行估计的基础,传统的SOC估计方法是通过自身参数进行估算[3 ] ,主要包括:①放电法[21 ] ,一种实验室环境下可靠的锂电池SOC估计测试方法,将锂电池以恒定电流持续放电至截止条件,将放电时间和放电电流相乘,便可得到放出的电量,进而可以计算出电池SOC值;②开路电压法[22 ] ,将锂电池进行长时间的静置,测量其开路电压和SOC,通过拟合电池开路电压与SOC的函数关系,然后通过该曲线对锂电池的SOC进行估计;③电导法[23 ] ,类似开路电压法,通过对锂电池电导值跟踪、测试,挖掘锂电池电导值与SOC之间的关系,归纳出映射规律实现对SOC估计;④交流阻抗法[24 ] ,类似于电导法,不同之处在于该方法对锂电池的阻抗进行跟踪测试;⑤安时积分法[4 ] ,是一种可用于在线检测的粗放式锂电池SOC计算方法,以电荷量是电流在时间上的积分为理论基础,在确定初始电量后对锂电池的充放电电流进行积分,再用初始电量加上或减去充放电获得或失去的电量,便可得到锂电池的实时容量,进而计算实时SOC,如公式(2) 所示.对比上述各类方法优缺点,如表3 所示. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
2
... 对锂电池可用容量的准确估计是对其SOC进行估计的基础,传统的SOC估计方法是通过自身参数进行估算[3 ] ,主要包括:①放电法[21 ] ,一种实验室环境下可靠的锂电池SOC估计测试方法,将锂电池以恒定电流持续放电至截止条件,将放电时间和放电电流相乘,便可得到放出的电量,进而可以计算出电池SOC值;②开路电压法[22 ] ,将锂电池进行长时间的静置,测量其开路电压和SOC,通过拟合电池开路电压与SOC的函数关系,然后通过该曲线对锂电池的SOC进行估计;③电导法[23 ] ,类似开路电压法,通过对锂电池电导值跟踪、测试,挖掘锂电池电导值与SOC之间的关系,归纳出映射规律实现对SOC估计;④交流阻抗法[24 ] ,类似于电导法,不同之处在于该方法对锂电池的阻抗进行跟踪测试;⑤安时积分法[4 ] ,是一种可用于在线检测的粗放式锂电池SOC计算方法,以电荷量是电流在时间上的积分为理论基础,在确定初始电量后对锂电池的充放电电流进行积分,再用初始电量加上或减去充放电获得或失去的电量,便可得到锂电池的实时容量,进而计算实时SOC,如公式(2) 所示.对比上述各类方法优缺点,如表3 所示. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
2
... 对锂电池可用容量的准确估计是对其SOC进行估计的基础,传统的SOC估计方法是通过自身参数进行估算[3 ] ,主要包括:①放电法[21 ] ,一种实验室环境下可靠的锂电池SOC估计测试方法,将锂电池以恒定电流持续放电至截止条件,将放电时间和放电电流相乘,便可得到放出的电量,进而可以计算出电池SOC值;②开路电压法[22 ] ,将锂电池进行长时间的静置,测量其开路电压和SOC,通过拟合电池开路电压与SOC的函数关系,然后通过该曲线对锂电池的SOC进行估计;③电导法[23 ] ,类似开路电压法,通过对锂电池电导值跟踪、测试,挖掘锂电池电导值与SOC之间的关系,归纳出映射规律实现对SOC估计;④交流阻抗法[24 ] ,类似于电导法,不同之处在于该方法对锂电池的阻抗进行跟踪测试;⑤安时积分法[4 ] ,是一种可用于在线检测的粗放式锂电池SOC计算方法,以电荷量是电流在时间上的积分为理论基础,在确定初始电量后对锂电池的充放电电流进行积分,再用初始电量加上或减去充放电获得或失去的电量,便可得到锂电池的实时容量,进而计算实时SOC,如公式(2) 所示.对比上述各类方法优缺点,如表3 所示. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
2
... 对锂电池可用容量的准确估计是对其SOC进行估计的基础,传统的SOC估计方法是通过自身参数进行估算[3 ] ,主要包括:①放电法[21 ] ,一种实验室环境下可靠的锂电池SOC估计测试方法,将锂电池以恒定电流持续放电至截止条件,将放电时间和放电电流相乘,便可得到放出的电量,进而可以计算出电池SOC值;②开路电压法[22 ] ,将锂电池进行长时间的静置,测量其开路电压和SOC,通过拟合电池开路电压与SOC的函数关系,然后通过该曲线对锂电池的SOC进行估计;③电导法[23 ] ,类似开路电压法,通过对锂电池电导值跟踪、测试,挖掘锂电池电导值与SOC之间的关系,归纳出映射规律实现对SOC估计;④交流阻抗法[24 ] ,类似于电导法,不同之处在于该方法对锂电池的阻抗进行跟踪测试;⑤安时积分法[4 ] ,是一种可用于在线检测的粗放式锂电池SOC计算方法,以电荷量是电流在时间上的积分为理论基础,在确定初始电量后对锂电池的充放电电流进行积分,再用初始电量加上或减去充放电获得或失去的电量,便可得到锂电池的实时容量,进而计算实时SOC,如公式(2) 所示.对比上述各类方法优缺点,如表3 所示. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
4
... 对锂电池可用容量的准确估计是对其SOC进行估计的基础,传统的SOC估计方法是通过自身参数进行估算[3 ] ,主要包括:①放电法[21 ] ,一种实验室环境下可靠的锂电池SOC估计测试方法,将锂电池以恒定电流持续放电至截止条件,将放电时间和放电电流相乘,便可得到放出的电量,进而可以计算出电池SOC值;②开路电压法[22 ] ,将锂电池进行长时间的静置,测量其开路电压和SOC,通过拟合电池开路电压与SOC的函数关系,然后通过该曲线对锂电池的SOC进行估计;③电导法[23 ] ,类似开路电压法,通过对锂电池电导值跟踪、测试,挖掘锂电池电导值与SOC之间的关系,归纳出映射规律实现对SOC估计;④交流阻抗法[24 ] ,类似于电导法,不同之处在于该方法对锂电池的阻抗进行跟踪测试;⑤安时积分法[4 ] ,是一种可用于在线检测的粗放式锂电池SOC计算方法,以电荷量是电流在时间上的积分为理论基础,在确定初始电量后对锂电池的充放电电流进行积分,再用初始电量加上或减去充放电获得或失去的电量,便可得到锂电池的实时容量,进而计算实时SOC,如公式(2) 所示.对比上述各类方法优缺点,如表3 所示. ...
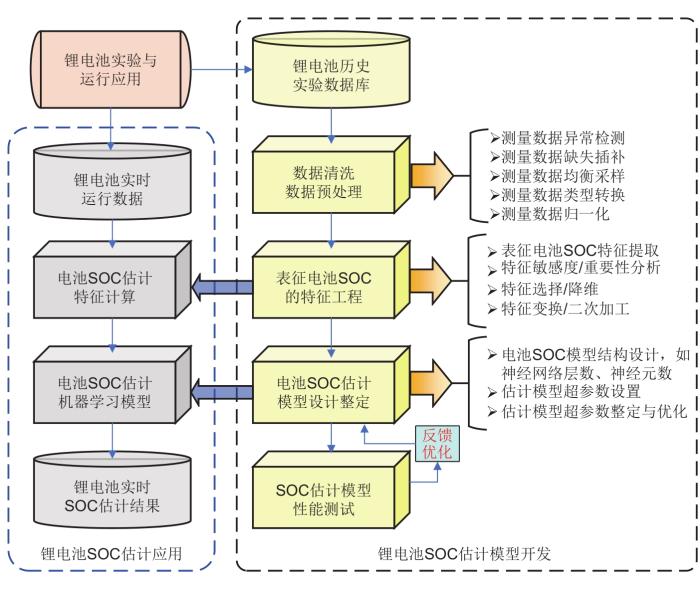
... 基于锂电池模型的SOC估计方法依赖于锂电池模型且难以反映出电池演变过程的参数变化,而基于锂电池数据驱动的SOC方法尽管可以不考虑锂电池模型,仅从锂电池测试数据本身挖掘出测量至SOC的映射关系,可以反映出锂电池演变过程规律,但电池数据数量和质量对锂电池SOC估计精度的影响巨大,且优质的电池数据难以保障.为了克服两种方式的不足,并充分发挥各自的估计优势,近年来国内外研究人员对两者的混合估计方法开展了大量研究.其中,一种主流的混合思路是基于数据驱动以及基于模型驱动的算法均可作为对方的辅助方法,如文献[73 ]使用极限学习机(extreme learning machine,ELM)预测SOC估计误差,并修正安时积分法的SOC估计结果,估计精度获得了较大提升;文献[23 ]和[74]分别利用神经网络和支持向量机数据驱动算法修正卡尔曼滤波算法的SOC估计结果,提高了估计精度,形成了数模混合驱动的SOC估计技术;而另一种混合思路在于将卡尔曼等状态估计算法用于基于电池数据SOC估计的模型参数优化之中,如文献[75 ]利用卡尔曼滤波训练神经网络权值及阈值,所得神经网络同样具有好的SOC预测效果.此外,还有数据驱动以及模型驱动算法的并行联合应用,如文献[76 ]中建立了长短时记忆网络与卡尔曼滤波的联合估计架构,实现了二者的并列联合估计.表7 展示了基于电池模型驱动和基于电池数据驱动的多种锂电池SOC估计融合方法,论述了不同融合技术的特点与优势. ...
... BP[23 ] ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
4
... 对锂电池可用容量的准确估计是对其SOC进行估计的基础,传统的SOC估计方法是通过自身参数进行估算[3 ] ,主要包括:①放电法[21 ] ,一种实验室环境下可靠的锂电池SOC估计测试方法,将锂电池以恒定电流持续放电至截止条件,将放电时间和放电电流相乘,便可得到放出的电量,进而可以计算出电池SOC值;②开路电压法[22 ] ,将锂电池进行长时间的静置,测量其开路电压和SOC,通过拟合电池开路电压与SOC的函数关系,然后通过该曲线对锂电池的SOC进行估计;③电导法[23 ] ,类似开路电压法,通过对锂电池电导值跟踪、测试,挖掘锂电池电导值与SOC之间的关系,归纳出映射规律实现对SOC估计;④交流阻抗法[24 ] ,类似于电导法,不同之处在于该方法对锂电池的阻抗进行跟踪测试;⑤安时积分法[4 ] ,是一种可用于在线检测的粗放式锂电池SOC计算方法,以电荷量是电流在时间上的积分为理论基础,在确定初始电量后对锂电池的充放电电流进行积分,再用初始电量加上或减去充放电获得或失去的电量,便可得到锂电池的实时容量,进而计算实时SOC,如公式(2) 所示.对比上述各类方法优缺点,如表3 所示. ...
... 基于锂电池模型的SOC估计方法依赖于锂电池模型且难以反映出电池演变过程的参数变化,而基于锂电池数据驱动的SOC方法尽管可以不考虑锂电池模型,仅从锂电池测试数据本身挖掘出测量至SOC的映射关系,可以反映出锂电池演变过程规律,但电池数据数量和质量对锂电池SOC估计精度的影响巨大,且优质的电池数据难以保障.为了克服两种方式的不足,并充分发挥各自的估计优势,近年来国内外研究人员对两者的混合估计方法开展了大量研究.其中,一种主流的混合思路是基于数据驱动以及基于模型驱动的算法均可作为对方的辅助方法,如文献[73 ]使用极限学习机(extreme learning machine,ELM)预测SOC估计误差,并修正安时积分法的SOC估计结果,估计精度获得了较大提升;文献[23 ]和[74]分别利用神经网络和支持向量机数据驱动算法修正卡尔曼滤波算法的SOC估计结果,提高了估计精度,形成了数模混合驱动的SOC估计技术;而另一种混合思路在于将卡尔曼等状态估计算法用于基于电池数据SOC估计的模型参数优化之中,如文献[75 ]利用卡尔曼滤波训练神经网络权值及阈值,所得神经网络同样具有好的SOC预测效果.此外,还有数据驱动以及模型驱动算法的并行联合应用,如文献[76 ]中建立了长短时记忆网络与卡尔曼滤波的联合估计架构,实现了二者的并列联合估计.表7 展示了基于电池模型驱动和基于电池数据驱动的多种锂电池SOC估计融合方法,论述了不同融合技术的特点与优势. ...
... BP[23 ] ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
2
... 对锂电池可用容量的准确估计是对其SOC进行估计的基础,传统的SOC估计方法是通过自身参数进行估算[3 ] ,主要包括:①放电法[21 ] ,一种实验室环境下可靠的锂电池SOC估计测试方法,将锂电池以恒定电流持续放电至截止条件,将放电时间和放电电流相乘,便可得到放出的电量,进而可以计算出电池SOC值;②开路电压法[22 ] ,将锂电池进行长时间的静置,测量其开路电压和SOC,通过拟合电池开路电压与SOC的函数关系,然后通过该曲线对锂电池的SOC进行估计;③电导法[23 ] ,类似开路电压法,通过对锂电池电导值跟踪、测试,挖掘锂电池电导值与SOC之间的关系,归纳出映射规律实现对SOC估计;④交流阻抗法[24 ] ,类似于电导法,不同之处在于该方法对锂电池的阻抗进行跟踪测试;⑤安时积分法[4 ] ,是一种可用于在线检测的粗放式锂电池SOC计算方法,以电荷量是电流在时间上的积分为理论基础,在确定初始电量后对锂电池的充放电电流进行积分,再用初始电量加上或减去充放电获得或失去的电量,便可得到锂电池的实时容量,进而计算实时SOC,如公式(2) 所示.对比上述各类方法优缺点,如表3 所示. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
2
... 对锂电池可用容量的准确估计是对其SOC进行估计的基础,传统的SOC估计方法是通过自身参数进行估算[3 ] ,主要包括:①放电法[21 ] ,一种实验室环境下可靠的锂电池SOC估计测试方法,将锂电池以恒定电流持续放电至截止条件,将放电时间和放电电流相乘,便可得到放出的电量,进而可以计算出电池SOC值;②开路电压法[22 ] ,将锂电池进行长时间的静置,测量其开路电压和SOC,通过拟合电池开路电压与SOC的函数关系,然后通过该曲线对锂电池的SOC进行估计;③电导法[23 ] ,类似开路电压法,通过对锂电池电导值跟踪、测试,挖掘锂电池电导值与SOC之间的关系,归纳出映射规律实现对SOC估计;④交流阻抗法[24 ] ,类似于电导法,不同之处在于该方法对锂电池的阻抗进行跟踪测试;⑤安时积分法[4 ] ,是一种可用于在线检测的粗放式锂电池SOC计算方法,以电荷量是电流在时间上的积分为理论基础,在确定初始电量后对锂电池的充放电电流进行积分,再用初始电量加上或减去充放电获得或失去的电量,便可得到锂电池的实时容量,进而计算实时SOC,如公式(2) 所示.对比上述各类方法优缺点,如表3 所示. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
1
... 目前,国内外专家学者围绕锂电池的电化学行为特征描述和数学建模已有较多研究成果[25 ] ,已有研究方法可分为以下三大类:①基于电池电化学过程的机理法,主要包括电化学模型[26 ] 和电化学阻抗模型[27 ] ,根据电化学反应过程描述电池电压、SOC和交流阻抗变化;②基于等效集总电气参数的等效电路法,将电池等效为二端口网络,以电源、电阻、电容等电气元件模拟电池特性,根据电气元件差异经典等效电路模型有Thevenin模型[28 ] 、PNGV模型[29 ] 、DP模型[30 ] 以及GNL模型[31 ] 等;③基于数据挖掘的黑箱模型,通过测量锂电池大量外特性数据,将机器学习等技术用于构建电池测量变量与输出变量的函数映射关系,其中以神经网络[32 ] 应用最为广泛.表4 展示了上述各种锂电池建模方法的典型结构以及优缺点对比. ...
1
... 目前,国内外专家学者围绕锂电池的电化学行为特征描述和数学建模已有较多研究成果[25 ] ,已有研究方法可分为以下三大类:①基于电池电化学过程的机理法,主要包括电化学模型[26 ] 和电化学阻抗模型[27 ] ,根据电化学反应过程描述电池电压、SOC和交流阻抗变化;②基于等效集总电气参数的等效电路法,将电池等效为二端口网络,以电源、电阻、电容等电气元件模拟电池特性,根据电气元件差异经典等效电路模型有Thevenin模型[28 ] 、PNGV模型[29 ] 、DP模型[30 ] 以及GNL模型[31 ] 等;③基于数据挖掘的黑箱模型,通过测量锂电池大量外特性数据,将机器学习等技术用于构建电池测量变量与输出变量的函数映射关系,其中以神经网络[32 ] 应用最为广泛.表4 展示了上述各种锂电池建模方法的典型结构以及优缺点对比. ...
1
... 目前,国内外专家学者围绕锂电池的电化学行为特征描述和数学建模已有较多研究成果[25 ] ,已有研究方法可分为以下三大类:①基于电池电化学过程的机理法,主要包括电化学模型[26 ] 和电化学阻抗模型[27 ] ,根据电化学反应过程描述电池电压、SOC和交流阻抗变化;②基于等效集总电气参数的等效电路法,将电池等效为二端口网络,以电源、电阻、电容等电气元件模拟电池特性,根据电气元件差异经典等效电路模型有Thevenin模型[28 ] 、PNGV模型[29 ] 、DP模型[30 ] 以及GNL模型[31 ] 等;③基于数据挖掘的黑箱模型,通过测量锂电池大量外特性数据,将机器学习等技术用于构建电池测量变量与输出变量的函数映射关系,其中以神经网络[32 ] 应用最为广泛.表4 展示了上述各种锂电池建模方法的典型结构以及优缺点对比. ...
1
... 目前,国内外专家学者围绕锂电池的电化学行为特征描述和数学建模已有较多研究成果[25 ] ,已有研究方法可分为以下三大类:①基于电池电化学过程的机理法,主要包括电化学模型[26 ] 和电化学阻抗模型[27 ] ,根据电化学反应过程描述电池电压、SOC和交流阻抗变化;②基于等效集总电气参数的等效电路法,将电池等效为二端口网络,以电源、电阻、电容等电气元件模拟电池特性,根据电气元件差异经典等效电路模型有Thevenin模型[28 ] 、PNGV模型[29 ] 、DP模型[30 ] 以及GNL模型[31 ] 等;③基于数据挖掘的黑箱模型,通过测量锂电池大量外特性数据,将机器学习等技术用于构建电池测量变量与输出变量的函数映射关系,其中以神经网络[32 ] 应用最为广泛.表4 展示了上述各种锂电池建模方法的典型结构以及优缺点对比. ...
1
... 目前,国内外专家学者围绕锂电池的电化学行为特征描述和数学建模已有较多研究成果[25 ] ,已有研究方法可分为以下三大类:①基于电池电化学过程的机理法,主要包括电化学模型[26 ] 和电化学阻抗模型[27 ] ,根据电化学反应过程描述电池电压、SOC和交流阻抗变化;②基于等效集总电气参数的等效电路法,将电池等效为二端口网络,以电源、电阻、电容等电气元件模拟电池特性,根据电气元件差异经典等效电路模型有Thevenin模型[28 ] 、PNGV模型[29 ] 、DP模型[30 ] 以及GNL模型[31 ] 等;③基于数据挖掘的黑箱模型,通过测量锂电池大量外特性数据,将机器学习等技术用于构建电池测量变量与输出变量的函数映射关系,其中以神经网络[32 ] 应用最为广泛.表4 展示了上述各种锂电池建模方法的典型结构以及优缺点对比. ...
1
... 目前,国内外专家学者围绕锂电池的电化学行为特征描述和数学建模已有较多研究成果[25 ] ,已有研究方法可分为以下三大类:①基于电池电化学过程的机理法,主要包括电化学模型[26 ] 和电化学阻抗模型[27 ] ,根据电化学反应过程描述电池电压、SOC和交流阻抗变化;②基于等效集总电气参数的等效电路法,将电池等效为二端口网络,以电源、电阻、电容等电气元件模拟电池特性,根据电气元件差异经典等效电路模型有Thevenin模型[28 ] 、PNGV模型[29 ] 、DP模型[30 ] 以及GNL模型[31 ] 等;③基于数据挖掘的黑箱模型,通过测量锂电池大量外特性数据,将机器学习等技术用于构建电池测量变量与输出变量的函数映射关系,其中以神经网络[32 ] 应用最为广泛.表4 展示了上述各种锂电池建模方法的典型结构以及优缺点对比. ...
1
... 目前,国内外专家学者围绕锂电池的电化学行为特征描述和数学建模已有较多研究成果[25 ] ,已有研究方法可分为以下三大类:①基于电池电化学过程的机理法,主要包括电化学模型[26 ] 和电化学阻抗模型[27 ] ,根据电化学反应过程描述电池电压、SOC和交流阻抗变化;②基于等效集总电气参数的等效电路法,将电池等效为二端口网络,以电源、电阻、电容等电气元件模拟电池特性,根据电气元件差异经典等效电路模型有Thevenin模型[28 ] 、PNGV模型[29 ] 、DP模型[30 ] 以及GNL模型[31 ] 等;③基于数据挖掘的黑箱模型,通过测量锂电池大量外特性数据,将机器学习等技术用于构建电池测量变量与输出变量的函数映射关系,其中以神经网络[32 ] 应用最为广泛.表4 展示了上述各种锂电池建模方法的典型结构以及优缺点对比. ...
1
... 目前,国内外专家学者围绕锂电池的电化学行为特征描述和数学建模已有较多研究成果[25 ] ,已有研究方法可分为以下三大类:①基于电池电化学过程的机理法,主要包括电化学模型[26 ] 和电化学阻抗模型[27 ] ,根据电化学反应过程描述电池电压、SOC和交流阻抗变化;②基于等效集总电气参数的等效电路法,将电池等效为二端口网络,以电源、电阻、电容等电气元件模拟电池特性,根据电气元件差异经典等效电路模型有Thevenin模型[28 ] 、PNGV模型[29 ] 、DP模型[30 ] 以及GNL模型[31 ] 等;③基于数据挖掘的黑箱模型,通过测量锂电池大量外特性数据,将机器学习等技术用于构建电池测量变量与输出变量的函数映射关系,其中以神经网络[32 ] 应用最为广泛.表4 展示了上述各种锂电池建模方法的典型结构以及优缺点对比. ...
1
... 目前,国内外专家学者围绕锂电池的电化学行为特征描述和数学建模已有较多研究成果[25 ] ,已有研究方法可分为以下三大类:①基于电池电化学过程的机理法,主要包括电化学模型[26 ] 和电化学阻抗模型[27 ] ,根据电化学反应过程描述电池电压、SOC和交流阻抗变化;②基于等效集总电气参数的等效电路法,将电池等效为二端口网络,以电源、电阻、电容等电气元件模拟电池特性,根据电气元件差异经典等效电路模型有Thevenin模型[28 ] 、PNGV模型[29 ] 、DP模型[30 ] 以及GNL模型[31 ] 等;③基于数据挖掘的黑箱模型,通过测量锂电池大量外特性数据,将机器学习等技术用于构建电池测量变量与输出变量的函数映射关系,其中以神经网络[32 ] 应用最为广泛.表4 展示了上述各种锂电池建模方法的典型结构以及优缺点对比. ...
1
... 目前,国内外专家学者围绕锂电池的电化学行为特征描述和数学建模已有较多研究成果[25 ] ,已有研究方法可分为以下三大类:①基于电池电化学过程的机理法,主要包括电化学模型[26 ] 和电化学阻抗模型[27 ] ,根据电化学反应过程描述电池电压、SOC和交流阻抗变化;②基于等效集总电气参数的等效电路法,将电池等效为二端口网络,以电源、电阻、电容等电气元件模拟电池特性,根据电气元件差异经典等效电路模型有Thevenin模型[28 ] 、PNGV模型[29 ] 、DP模型[30 ] 以及GNL模型[31 ] 等;③基于数据挖掘的黑箱模型,通过测量锂电池大量外特性数据,将机器学习等技术用于构建电池测量变量与输出变量的函数映射关系,其中以神经网络[32 ] 应用最为广泛.表4 展示了上述各种锂电池建模方法的典型结构以及优缺点对比. ...
1
... 目前,国内外专家学者围绕锂电池的电化学行为特征描述和数学建模已有较多研究成果[25 ] ,已有研究方法可分为以下三大类:①基于电池电化学过程的机理法,主要包括电化学模型[26 ] 和电化学阻抗模型[27 ] ,根据电化学反应过程描述电池电压、SOC和交流阻抗变化;②基于等效集总电气参数的等效电路法,将电池等效为二端口网络,以电源、电阻、电容等电气元件模拟电池特性,根据电气元件差异经典等效电路模型有Thevenin模型[28 ] 、PNGV模型[29 ] 、DP模型[30 ] 以及GNL模型[31 ] 等;③基于数据挖掘的黑箱模型,通过测量锂电池大量外特性数据,将机器学习等技术用于构建电池测量变量与输出变量的函数映射关系,其中以神经网络[32 ] 应用最为广泛.表4 展示了上述各种锂电池建模方法的典型结构以及优缺点对比. ...
1
... 目前,国内外专家学者围绕锂电池的电化学行为特征描述和数学建模已有较多研究成果[25 ] ,已有研究方法可分为以下三大类:①基于电池电化学过程的机理法,主要包括电化学模型[26 ] 和电化学阻抗模型[27 ] ,根据电化学反应过程描述电池电压、SOC和交流阻抗变化;②基于等效集总电气参数的等效电路法,将电池等效为二端口网络,以电源、电阻、电容等电气元件模拟电池特性,根据电气元件差异经典等效电路模型有Thevenin模型[28 ] 、PNGV模型[29 ] 、DP模型[30 ] 以及GNL模型[31 ] 等;③基于数据挖掘的黑箱模型,通过测量锂电池大量外特性数据,将机器学习等技术用于构建电池测量变量与输出变量的函数映射关系,其中以神经网络[32 ] 应用最为广泛.表4 展示了上述各种锂电池建模方法的典型结构以及优缺点对比. ...
1
... 目前,国内外专家学者围绕锂电池的电化学行为特征描述和数学建模已有较多研究成果[25 ] ,已有研究方法可分为以下三大类:①基于电池电化学过程的机理法,主要包括电化学模型[26 ] 和电化学阻抗模型[27 ] ,根据电化学反应过程描述电池电压、SOC和交流阻抗变化;②基于等效集总电气参数的等效电路法,将电池等效为二端口网络,以电源、电阻、电容等电气元件模拟电池特性,根据电气元件差异经典等效电路模型有Thevenin模型[28 ] 、PNGV模型[29 ] 、DP模型[30 ] 以及GNL模型[31 ] 等;③基于数据挖掘的黑箱模型,通过测量锂电池大量外特性数据,将机器学习等技术用于构建电池测量变量与输出变量的函数映射关系,其中以神经网络[32 ] 应用最为广泛.表4 展示了上述各种锂电池建模方法的典型结构以及优缺点对比. ...
1
... 目前,国内外专家学者围绕锂电池的电化学行为特征描述和数学建模已有较多研究成果[25 ] ,已有研究方法可分为以下三大类:①基于电池电化学过程的机理法,主要包括电化学模型[26 ] 和电化学阻抗模型[27 ] ,根据电化学反应过程描述电池电压、SOC和交流阻抗变化;②基于等效集总电气参数的等效电路法,将电池等效为二端口网络,以电源、电阻、电容等电气元件模拟电池特性,根据电气元件差异经典等效电路模型有Thevenin模型[28 ] 、PNGV模型[29 ] 、DP模型[30 ] 以及GNL模型[31 ] 等;③基于数据挖掘的黑箱模型,通过测量锂电池大量外特性数据,将机器学习等技术用于构建电池测量变量与输出变量的函数映射关系,其中以神经网络[32 ] 应用最为广泛.表4 展示了上述各种锂电池建模方法的典型结构以及优缺点对比. ...
1
... 目前,国内外专家学者围绕锂电池的电化学行为特征描述和数学建模已有较多研究成果[25 ] ,已有研究方法可分为以下三大类:①基于电池电化学过程的机理法,主要包括电化学模型[26 ] 和电化学阻抗模型[27 ] ,根据电化学反应过程描述电池电压、SOC和交流阻抗变化;②基于等效集总电气参数的等效电路法,将电池等效为二端口网络,以电源、电阻、电容等电气元件模拟电池特性,根据电气元件差异经典等效电路模型有Thevenin模型[28 ] 、PNGV模型[29 ] 、DP模型[30 ] 以及GNL模型[31 ] 等;③基于数据挖掘的黑箱模型,通过测量锂电池大量外特性数据,将机器学习等技术用于构建电池测量变量与输出变量的函数映射关系,其中以神经网络[32 ] 应用最为广泛.表4 展示了上述各种锂电池建模方法的典型结构以及优缺点对比. ...
1
... 目前,国内外专家学者围绕锂电池的电化学行为特征描述和数学建模已有较多研究成果[25 ] ,已有研究方法可分为以下三大类:①基于电池电化学过程的机理法,主要包括电化学模型[26 ] 和电化学阻抗模型[27 ] ,根据电化学反应过程描述电池电压、SOC和交流阻抗变化;②基于等效集总电气参数的等效电路法,将电池等效为二端口网络,以电源、电阻、电容等电气元件模拟电池特性,根据电气元件差异经典等效电路模型有Thevenin模型[28 ] 、PNGV模型[29 ] 、DP模型[30 ] 以及GNL模型[31 ] 等;③基于数据挖掘的黑箱模型,通过测量锂电池大量外特性数据,将机器学习等技术用于构建电池测量变量与输出变量的函数映射关系,其中以神经网络[32 ] 应用最为广泛.表4 展示了上述各种锂电池建模方法的典型结构以及优缺点对比. ...
1
... 卡尔曼滤波(Kalman filter,KF)及其改进型算法是一种面向线性定常系统状态估计的最优化递推估计方法,被广泛应用于对系统内部难以或者无法直接测量的状态变量的估计之中[33 ] .在锂电池SOC估计应用中,研究人员以锂电池数学模型构筑的电池系统状态空间为基础,形成对锂电池SOC的先验预测,再利用可测量的电池电压、温度、电流等变量及卡尔曼增益矩阵更新锂电池SOC的后验估计值,获得锂电池较为准确的实时SOC估计值[34 ] .锂电池系统X k + 1 = A X k + B I o k U k + 1 = H X k
1
... 卡尔曼滤波(Kalman filter,KF)及其改进型算法是一种面向线性定常系统状态估计的最优化递推估计方法,被广泛应用于对系统内部难以或者无法直接测量的状态变量的估计之中[33 ] .在锂电池SOC估计应用中,研究人员以锂电池数学模型构筑的电池系统状态空间为基础,形成对锂电池SOC的先验预测,再利用可测量的电池电压、温度、电流等变量及卡尔曼增益矩阵更新锂电池SOC的后验估计值,获得锂电池较为准确的实时SOC估计值[34 ] .锂电池系统X k + 1 = A X k + B I o k U k + 1 = H X k
1
... 卡尔曼滤波(Kalman filter,KF)及其改进型算法是一种面向线性定常系统状态估计的最优化递推估计方法,被广泛应用于对系统内部难以或者无法直接测量的状态变量的估计之中[33 ] .在锂电池SOC估计应用中,研究人员以锂电池数学模型构筑的电池系统状态空间为基础,形成对锂电池SOC的先验预测,再利用可测量的电池电压、温度、电流等变量及卡尔曼增益矩阵更新锂电池SOC的后验估计值,获得锂电池较为准确的实时SOC估计值[34 ] .锂电池系统X k + 1 = A X k + B I o k U k + 1 = H X k
1
... 卡尔曼滤波(Kalman filter,KF)及其改进型算法是一种面向线性定常系统状态估计的最优化递推估计方法,被广泛应用于对系统内部难以或者无法直接测量的状态变量的估计之中[33 ] .在锂电池SOC估计应用中,研究人员以锂电池数学模型构筑的电池系统状态空间为基础,形成对锂电池SOC的先验预测,再利用可测量的电池电压、温度、电流等变量及卡尔曼增益矩阵更新锂电池SOC的后验估计值,获得锂电池较为准确的实时SOC估计值[34 ] .锂电池系统X k + 1 = A X k + B I o k U k + 1 = H X k
2
... 由于经典卡尔曼滤波算法仅适用于线性定常系统,而锂电池电化学过程表现为非线性、时变等复杂特点,经典卡尔曼滤波算法难以形成有效估计.因此,专家学者们围绕非线性系统下的状态估计问题对KF算法进行了多种改进,使其更适用于锂电池SOC估计应用.例如,文献[35 -36 ]借助泰勒级数展开对非线性系统线性化得到的拓展卡尔曼(extended kalman filter,EKF)滤波算法形成对锂电池SOC的准确观测,有效地将适用于线性系统的KF拓展至非线性系统之中;文献[37 -38 ]通过引入无迹变换,避免了非线性系统在泰勒级数展开时导致的估计精度损失,形成了锂电池SOC的无迹卡尔曼(unscented kalman filter,UKF)估计模型,获得了更为优异的估计精度;文献[39 ]提出容积卡尔曼滤波(cubature kalman filter,CKF)模型的锂电池SOC估计方式,克服了UKF在高维情况下滤波精度不高的问题.与此同时,部分研究者将自适应思想引入卡尔曼算法中,解决锂电池参数变化和外界干扰对估计精度的影响.如文献[40 -42 ]在EKF和UKF计算中加入了参数辨识步骤,形成了自适应卡尔曼(adaptive kalman filter,AKF)算法,可以实时响应电池参数变化导致SOC估计误差;文献[43 ]将在EKF中加入了模糊调节步骤,更为准确地 修正了外界噪声的变化对电池SOC估计的影响.除了上述解决锂电池非线性和参数时变特点以外的改进,为了拓展卡尔曼算法在锂电池状态估计中的应用范围,文献[44 -45 ]建立了双卡尔曼体系下的电池SOC观测模型,利用KF准确描述电池参数变化,同时辅助EKF估计电池SOC.表5 对比出了多种不同卡尔曼滤波及改进算法具有不同的优缺点. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
2
... 由于经典卡尔曼滤波算法仅适用于线性定常系统,而锂电池电化学过程表现为非线性、时变等复杂特点,经典卡尔曼滤波算法难以形成有效估计.因此,专家学者们围绕非线性系统下的状态估计问题对KF算法进行了多种改进,使其更适用于锂电池SOC估计应用.例如,文献[35 -36 ]借助泰勒级数展开对非线性系统线性化得到的拓展卡尔曼(extended kalman filter,EKF)滤波算法形成对锂电池SOC的准确观测,有效地将适用于线性系统的KF拓展至非线性系统之中;文献[37 -38 ]通过引入无迹变换,避免了非线性系统在泰勒级数展开时导致的估计精度损失,形成了锂电池SOC的无迹卡尔曼(unscented kalman filter,UKF)估计模型,获得了更为优异的估计精度;文献[39 ]提出容积卡尔曼滤波(cubature kalman filter,CKF)模型的锂电池SOC估计方式,克服了UKF在高维情况下滤波精度不高的问题.与此同时,部分研究者将自适应思想引入卡尔曼算法中,解决锂电池参数变化和外界干扰对估计精度的影响.如文献[40 -42 ]在EKF和UKF计算中加入了参数辨识步骤,形成了自适应卡尔曼(adaptive kalman filter,AKF)算法,可以实时响应电池参数变化导致SOC估计误差;文献[43 ]将在EKF中加入了模糊调节步骤,更为准确地 修正了外界噪声的变化对电池SOC估计的影响.除了上述解决锂电池非线性和参数时变特点以外的改进,为了拓展卡尔曼算法在锂电池状态估计中的应用范围,文献[44 -45 ]建立了双卡尔曼体系下的电池SOC观测模型,利用KF准确描述电池参数变化,同时辅助EKF估计电池SOC.表5 对比出了多种不同卡尔曼滤波及改进算法具有不同的优缺点. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
2
... 由于经典卡尔曼滤波算法仅适用于线性定常系统,而锂电池电化学过程表现为非线性、时变等复杂特点,经典卡尔曼滤波算法难以形成有效估计.因此,专家学者们围绕非线性系统下的状态估计问题对KF算法进行了多种改进,使其更适用于锂电池SOC估计应用.例如,文献[35 -36 ]借助泰勒级数展开对非线性系统线性化得到的拓展卡尔曼(extended kalman filter,EKF)滤波算法形成对锂电池SOC的准确观测,有效地将适用于线性系统的KF拓展至非线性系统之中;文献[37 -38 ]通过引入无迹变换,避免了非线性系统在泰勒级数展开时导致的估计精度损失,形成了锂电池SOC的无迹卡尔曼(unscented kalman filter,UKF)估计模型,获得了更为优异的估计精度;文献[39 ]提出容积卡尔曼滤波(cubature kalman filter,CKF)模型的锂电池SOC估计方式,克服了UKF在高维情况下滤波精度不高的问题.与此同时,部分研究者将自适应思想引入卡尔曼算法中,解决锂电池参数变化和外界干扰对估计精度的影响.如文献[40 -42 ]在EKF和UKF计算中加入了参数辨识步骤,形成了自适应卡尔曼(adaptive kalman filter,AKF)算法,可以实时响应电池参数变化导致SOC估计误差;文献[43 ]将在EKF中加入了模糊调节步骤,更为准确地 修正了外界噪声的变化对电池SOC估计的影响.除了上述解决锂电池非线性和参数时变特点以外的改进,为了拓展卡尔曼算法在锂电池状态估计中的应用范围,文献[44 -45 ]建立了双卡尔曼体系下的电池SOC观测模型,利用KF准确描述电池参数变化,同时辅助EKF估计电池SOC.表5 对比出了多种不同卡尔曼滤波及改进算法具有不同的优缺点. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
2
... 由于经典卡尔曼滤波算法仅适用于线性定常系统,而锂电池电化学过程表现为非线性、时变等复杂特点,经典卡尔曼滤波算法难以形成有效估计.因此,专家学者们围绕非线性系统下的状态估计问题对KF算法进行了多种改进,使其更适用于锂电池SOC估计应用.例如,文献[35 -36 ]借助泰勒级数展开对非线性系统线性化得到的拓展卡尔曼(extended kalman filter,EKF)滤波算法形成对锂电池SOC的准确观测,有效地将适用于线性系统的KF拓展至非线性系统之中;文献[37 -38 ]通过引入无迹变换,避免了非线性系统在泰勒级数展开时导致的估计精度损失,形成了锂电池SOC的无迹卡尔曼(unscented kalman filter,UKF)估计模型,获得了更为优异的估计精度;文献[39 ]提出容积卡尔曼滤波(cubature kalman filter,CKF)模型的锂电池SOC估计方式,克服了UKF在高维情况下滤波精度不高的问题.与此同时,部分研究者将自适应思想引入卡尔曼算法中,解决锂电池参数变化和外界干扰对估计精度的影响.如文献[40 -42 ]在EKF和UKF计算中加入了参数辨识步骤,形成了自适应卡尔曼(adaptive kalman filter,AKF)算法,可以实时响应电池参数变化导致SOC估计误差;文献[43 ]将在EKF中加入了模糊调节步骤,更为准确地 修正了外界噪声的变化对电池SOC估计的影响.除了上述解决锂电池非线性和参数时变特点以外的改进,为了拓展卡尔曼算法在锂电池状态估计中的应用范围,文献[44 -45 ]建立了双卡尔曼体系下的电池SOC观测模型,利用KF准确描述电池参数变化,同时辅助EKF估计电池SOC.表5 对比出了多种不同卡尔曼滤波及改进算法具有不同的优缺点. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
1
... 由于经典卡尔曼滤波算法仅适用于线性定常系统,而锂电池电化学过程表现为非线性、时变等复杂特点,经典卡尔曼滤波算法难以形成有效估计.因此,专家学者们围绕非线性系统下的状态估计问题对KF算法进行了多种改进,使其更适用于锂电池SOC估计应用.例如,文献[35 -36 ]借助泰勒级数展开对非线性系统线性化得到的拓展卡尔曼(extended kalman filter,EKF)滤波算法形成对锂电池SOC的准确观测,有效地将适用于线性系统的KF拓展至非线性系统之中;文献[37 -38 ]通过引入无迹变换,避免了非线性系统在泰勒级数展开时导致的估计精度损失,形成了锂电池SOC的无迹卡尔曼(unscented kalman filter,UKF)估计模型,获得了更为优异的估计精度;文献[39 ]提出容积卡尔曼滤波(cubature kalman filter,CKF)模型的锂电池SOC估计方式,克服了UKF在高维情况下滤波精度不高的问题.与此同时,部分研究者将自适应思想引入卡尔曼算法中,解决锂电池参数变化和外界干扰对估计精度的影响.如文献[40 -42 ]在EKF和UKF计算中加入了参数辨识步骤,形成了自适应卡尔曼(adaptive kalman filter,AKF)算法,可以实时响应电池参数变化导致SOC估计误差;文献[43 ]将在EKF中加入了模糊调节步骤,更为准确地 修正了外界噪声的变化对电池SOC估计的影响.除了上述解决锂电池非线性和参数时变特点以外的改进,为了拓展卡尔曼算法在锂电池状态估计中的应用范围,文献[44 -45 ]建立了双卡尔曼体系下的电池SOC观测模型,利用KF准确描述电池参数变化,同时辅助EKF估计电池SOC.表5 对比出了多种不同卡尔曼滤波及改进算法具有不同的优缺点. ...
1
... 由于经典卡尔曼滤波算法仅适用于线性定常系统,而锂电池电化学过程表现为非线性、时变等复杂特点,经典卡尔曼滤波算法难以形成有效估计.因此,专家学者们围绕非线性系统下的状态估计问题对KF算法进行了多种改进,使其更适用于锂电池SOC估计应用.例如,文献[35 -36 ]借助泰勒级数展开对非线性系统线性化得到的拓展卡尔曼(extended kalman filter,EKF)滤波算法形成对锂电池SOC的准确观测,有效地将适用于线性系统的KF拓展至非线性系统之中;文献[37 -38 ]通过引入无迹变换,避免了非线性系统在泰勒级数展开时导致的估计精度损失,形成了锂电池SOC的无迹卡尔曼(unscented kalman filter,UKF)估计模型,获得了更为优异的估计精度;文献[39 ]提出容积卡尔曼滤波(cubature kalman filter,CKF)模型的锂电池SOC估计方式,克服了UKF在高维情况下滤波精度不高的问题.与此同时,部分研究者将自适应思想引入卡尔曼算法中,解决锂电池参数变化和外界干扰对估计精度的影响.如文献[40 -42 ]在EKF和UKF计算中加入了参数辨识步骤,形成了自适应卡尔曼(adaptive kalman filter,AKF)算法,可以实时响应电池参数变化导致SOC估计误差;文献[43 ]将在EKF中加入了模糊调节步骤,更为准确地 修正了外界噪声的变化对电池SOC估计的影响.除了上述解决锂电池非线性和参数时变特点以外的改进,为了拓展卡尔曼算法在锂电池状态估计中的应用范围,文献[44 -45 ]建立了双卡尔曼体系下的电池SOC观测模型,利用KF准确描述电池参数变化,同时辅助EKF估计电池SOC.表5 对比出了多种不同卡尔曼滤波及改进算法具有不同的优缺点. ...
1
... 由于经典卡尔曼滤波算法仅适用于线性定常系统,而锂电池电化学过程表现为非线性、时变等复杂特点,经典卡尔曼滤波算法难以形成有效估计.因此,专家学者们围绕非线性系统下的状态估计问题对KF算法进行了多种改进,使其更适用于锂电池SOC估计应用.例如,文献[35 -36 ]借助泰勒级数展开对非线性系统线性化得到的拓展卡尔曼(extended kalman filter,EKF)滤波算法形成对锂电池SOC的准确观测,有效地将适用于线性系统的KF拓展至非线性系统之中;文献[37 -38 ]通过引入无迹变换,避免了非线性系统在泰勒级数展开时导致的估计精度损失,形成了锂电池SOC的无迹卡尔曼(unscented kalman filter,UKF)估计模型,获得了更为优异的估计精度;文献[39 ]提出容积卡尔曼滤波(cubature kalman filter,CKF)模型的锂电池SOC估计方式,克服了UKF在高维情况下滤波精度不高的问题.与此同时,部分研究者将自适应思想引入卡尔曼算法中,解决锂电池参数变化和外界干扰对估计精度的影响.如文献[40 -42 ]在EKF和UKF计算中加入了参数辨识步骤,形成了自适应卡尔曼(adaptive kalman filter,AKF)算法,可以实时响应电池参数变化导致SOC估计误差;文献[43 ]将在EKF中加入了模糊调节步骤,更为准确地 修正了外界噪声的变化对电池SOC估计的影响.除了上述解决锂电池非线性和参数时变特点以外的改进,为了拓展卡尔曼算法在锂电池状态估计中的应用范围,文献[44 -45 ]建立了双卡尔曼体系下的电池SOC观测模型,利用KF准确描述电池参数变化,同时辅助EKF估计电池SOC.表5 对比出了多种不同卡尔曼滤波及改进算法具有不同的优缺点. ...
1
... 由于经典卡尔曼滤波算法仅适用于线性定常系统,而锂电池电化学过程表现为非线性、时变等复杂特点,经典卡尔曼滤波算法难以形成有效估计.因此,专家学者们围绕非线性系统下的状态估计问题对KF算法进行了多种改进,使其更适用于锂电池SOC估计应用.例如,文献[35 -36 ]借助泰勒级数展开对非线性系统线性化得到的拓展卡尔曼(extended kalman filter,EKF)滤波算法形成对锂电池SOC的准确观测,有效地将适用于线性系统的KF拓展至非线性系统之中;文献[37 -38 ]通过引入无迹变换,避免了非线性系统在泰勒级数展开时导致的估计精度损失,形成了锂电池SOC的无迹卡尔曼(unscented kalman filter,UKF)估计模型,获得了更为优异的估计精度;文献[39 ]提出容积卡尔曼滤波(cubature kalman filter,CKF)模型的锂电池SOC估计方式,克服了UKF在高维情况下滤波精度不高的问题.与此同时,部分研究者将自适应思想引入卡尔曼算法中,解决锂电池参数变化和外界干扰对估计精度的影响.如文献[40 -42 ]在EKF和UKF计算中加入了参数辨识步骤,形成了自适应卡尔曼(adaptive kalman filter,AKF)算法,可以实时响应电池参数变化导致SOC估计误差;文献[43 ]将在EKF中加入了模糊调节步骤,更为准确地 修正了外界噪声的变化对电池SOC估计的影响.除了上述解决锂电池非线性和参数时变特点以外的改进,为了拓展卡尔曼算法在锂电池状态估计中的应用范围,文献[44 -45 ]建立了双卡尔曼体系下的电池SOC观测模型,利用KF准确描述电池参数变化,同时辅助EKF估计电池SOC.表5 对比出了多种不同卡尔曼滤波及改进算法具有不同的优缺点. ...
1
... 由于经典卡尔曼滤波算法仅适用于线性定常系统,而锂电池电化学过程表现为非线性、时变等复杂特点,经典卡尔曼滤波算法难以形成有效估计.因此,专家学者们围绕非线性系统下的状态估计问题对KF算法进行了多种改进,使其更适用于锂电池SOC估计应用.例如,文献[35 -36 ]借助泰勒级数展开对非线性系统线性化得到的拓展卡尔曼(extended kalman filter,EKF)滤波算法形成对锂电池SOC的准确观测,有效地将适用于线性系统的KF拓展至非线性系统之中;文献[37 -38 ]通过引入无迹变换,避免了非线性系统在泰勒级数展开时导致的估计精度损失,形成了锂电池SOC的无迹卡尔曼(unscented kalman filter,UKF)估计模型,获得了更为优异的估计精度;文献[39 ]提出容积卡尔曼滤波(cubature kalman filter,CKF)模型的锂电池SOC估计方式,克服了UKF在高维情况下滤波精度不高的问题.与此同时,部分研究者将自适应思想引入卡尔曼算法中,解决锂电池参数变化和外界干扰对估计精度的影响.如文献[40 -42 ]在EKF和UKF计算中加入了参数辨识步骤,形成了自适应卡尔曼(adaptive kalman filter,AKF)算法,可以实时响应电池参数变化导致SOC估计误差;文献[43 ]将在EKF中加入了模糊调节步骤,更为准确地 修正了外界噪声的变化对电池SOC估计的影响.除了上述解决锂电池非线性和参数时变特点以外的改进,为了拓展卡尔曼算法在锂电池状态估计中的应用范围,文献[44 -45 ]建立了双卡尔曼体系下的电池SOC观测模型,利用KF准确描述电池参数变化,同时辅助EKF估计电池SOC.表5 对比出了多种不同卡尔曼滤波及改进算法具有不同的优缺点. ...
1
... 由于经典卡尔曼滤波算法仅适用于线性定常系统,而锂电池电化学过程表现为非线性、时变等复杂特点,经典卡尔曼滤波算法难以形成有效估计.因此,专家学者们围绕非线性系统下的状态估计问题对KF算法进行了多种改进,使其更适用于锂电池SOC估计应用.例如,文献[35 -36 ]借助泰勒级数展开对非线性系统线性化得到的拓展卡尔曼(extended kalman filter,EKF)滤波算法形成对锂电池SOC的准确观测,有效地将适用于线性系统的KF拓展至非线性系统之中;文献[37 -38 ]通过引入无迹变换,避免了非线性系统在泰勒级数展开时导致的估计精度损失,形成了锂电池SOC的无迹卡尔曼(unscented kalman filter,UKF)估计模型,获得了更为优异的估计精度;文献[39 ]提出容积卡尔曼滤波(cubature kalman filter,CKF)模型的锂电池SOC估计方式,克服了UKF在高维情况下滤波精度不高的问题.与此同时,部分研究者将自适应思想引入卡尔曼算法中,解决锂电池参数变化和外界干扰对估计精度的影响.如文献[40 -42 ]在EKF和UKF计算中加入了参数辨识步骤,形成了自适应卡尔曼(adaptive kalman filter,AKF)算法,可以实时响应电池参数变化导致SOC估计误差;文献[43 ]将在EKF中加入了模糊调节步骤,更为准确地 修正了外界噪声的变化对电池SOC估计的影响.除了上述解决锂电池非线性和参数时变特点以外的改进,为了拓展卡尔曼算法在锂电池状态估计中的应用范围,文献[44 -45 ]建立了双卡尔曼体系下的电池SOC观测模型,利用KF准确描述电池参数变化,同时辅助EKF估计电池SOC.表5 对比出了多种不同卡尔曼滤波及改进算法具有不同的优缺点. ...
1
... 由于经典卡尔曼滤波算法仅适用于线性定常系统,而锂电池电化学过程表现为非线性、时变等复杂特点,经典卡尔曼滤波算法难以形成有效估计.因此,专家学者们围绕非线性系统下的状态估计问题对KF算法进行了多种改进,使其更适用于锂电池SOC估计应用.例如,文献[35 -36 ]借助泰勒级数展开对非线性系统线性化得到的拓展卡尔曼(extended kalman filter,EKF)滤波算法形成对锂电池SOC的准确观测,有效地将适用于线性系统的KF拓展至非线性系统之中;文献[37 -38 ]通过引入无迹变换,避免了非线性系统在泰勒级数展开时导致的估计精度损失,形成了锂电池SOC的无迹卡尔曼(unscented kalman filter,UKF)估计模型,获得了更为优异的估计精度;文献[39 ]提出容积卡尔曼滤波(cubature kalman filter,CKF)模型的锂电池SOC估计方式,克服了UKF在高维情况下滤波精度不高的问题.与此同时,部分研究者将自适应思想引入卡尔曼算法中,解决锂电池参数变化和外界干扰对估计精度的影响.如文献[40 -42 ]在EKF和UKF计算中加入了参数辨识步骤,形成了自适应卡尔曼(adaptive kalman filter,AKF)算法,可以实时响应电池参数变化导致SOC估计误差;文献[43 ]将在EKF中加入了模糊调节步骤,更为准确地 修正了外界噪声的变化对电池SOC估计的影响.除了上述解决锂电池非线性和参数时变特点以外的改进,为了拓展卡尔曼算法在锂电池状态估计中的应用范围,文献[44 -45 ]建立了双卡尔曼体系下的电池SOC观测模型,利用KF准确描述电池参数变化,同时辅助EKF估计电池SOC.表5 对比出了多种不同卡尔曼滤波及改进算法具有不同的优缺点. ...
2
... 由于经典卡尔曼滤波算法仅适用于线性定常系统,而锂电池电化学过程表现为非线性、时变等复杂特点,经典卡尔曼滤波算法难以形成有效估计.因此,专家学者们围绕非线性系统下的状态估计问题对KF算法进行了多种改进,使其更适用于锂电池SOC估计应用.例如,文献[35 -36 ]借助泰勒级数展开对非线性系统线性化得到的拓展卡尔曼(extended kalman filter,EKF)滤波算法形成对锂电池SOC的准确观测,有效地将适用于线性系统的KF拓展至非线性系统之中;文献[37 -38 ]通过引入无迹变换,避免了非线性系统在泰勒级数展开时导致的估计精度损失,形成了锂电池SOC的无迹卡尔曼(unscented kalman filter,UKF)估计模型,获得了更为优异的估计精度;文献[39 ]提出容积卡尔曼滤波(cubature kalman filter,CKF)模型的锂电池SOC估计方式,克服了UKF在高维情况下滤波精度不高的问题.与此同时,部分研究者将自适应思想引入卡尔曼算法中,解决锂电池参数变化和外界干扰对估计精度的影响.如文献[40 -42 ]在EKF和UKF计算中加入了参数辨识步骤,形成了自适应卡尔曼(adaptive kalman filter,AKF)算法,可以实时响应电池参数变化导致SOC估计误差;文献[43 ]将在EKF中加入了模糊调节步骤,更为准确地 修正了外界噪声的变化对电池SOC估计的影响.除了上述解决锂电池非线性和参数时变特点以外的改进,为了拓展卡尔曼算法在锂电池状态估计中的应用范围,文献[44 -45 ]建立了双卡尔曼体系下的电池SOC观测模型,利用KF准确描述电池参数变化,同时辅助EKF估计电池SOC.表5 对比出了多种不同卡尔曼滤波及改进算法具有不同的优缺点. ...
... 除了上述单独对卡尔曼估计算法改进以外,部分研究者提出适当组合电池SOC卡尔曼类估计模型以达到更佳的估计精度.如文献[46 ]将EKF和平滑可变结构滤波(SVSF)组合,利用EKF和SVSF分别完成电池参数辨识和SOC估计任务,相比于单一EKF电池SOC估计精度获得了提升;文献[47 ]利用两层UKF互相嵌套的方式,形成双层架构解决单一UKF在高阶非线性系统估计精度低的问题;文献[48 ]提出考虑电池寿命衰退影响的卡尔曼滤波并行结构,完成电池SOC估计及修正;文献[42 ]为了弥补卡尔曼滤波鲁棒性差以及H无穷滤波依赖初值的问题,提出一种两者联合SOC估计方式,保证SOC估计误差被可靠地限制在2%以内. ...
2
... 由于经典卡尔曼滤波算法仅适用于线性定常系统,而锂电池电化学过程表现为非线性、时变等复杂特点,经典卡尔曼滤波算法难以形成有效估计.因此,专家学者们围绕非线性系统下的状态估计问题对KF算法进行了多种改进,使其更适用于锂电池SOC估计应用.例如,文献[35 -36 ]借助泰勒级数展开对非线性系统线性化得到的拓展卡尔曼(extended kalman filter,EKF)滤波算法形成对锂电池SOC的准确观测,有效地将适用于线性系统的KF拓展至非线性系统之中;文献[37 -38 ]通过引入无迹变换,避免了非线性系统在泰勒级数展开时导致的估计精度损失,形成了锂电池SOC的无迹卡尔曼(unscented kalman filter,UKF)估计模型,获得了更为优异的估计精度;文献[39 ]提出容积卡尔曼滤波(cubature kalman filter,CKF)模型的锂电池SOC估计方式,克服了UKF在高维情况下滤波精度不高的问题.与此同时,部分研究者将自适应思想引入卡尔曼算法中,解决锂电池参数变化和外界干扰对估计精度的影响.如文献[40 -42 ]在EKF和UKF计算中加入了参数辨识步骤,形成了自适应卡尔曼(adaptive kalman filter,AKF)算法,可以实时响应电池参数变化导致SOC估计误差;文献[43 ]将在EKF中加入了模糊调节步骤,更为准确地 修正了外界噪声的变化对电池SOC估计的影响.除了上述解决锂电池非线性和参数时变特点以外的改进,为了拓展卡尔曼算法在锂电池状态估计中的应用范围,文献[44 -45 ]建立了双卡尔曼体系下的电池SOC观测模型,利用KF准确描述电池参数变化,同时辅助EKF估计电池SOC.表5 对比出了多种不同卡尔曼滤波及改进算法具有不同的优缺点. ...
... 除了上述单独对卡尔曼估计算法改进以外,部分研究者提出适当组合电池SOC卡尔曼类估计模型以达到更佳的估计精度.如文献[46 ]将EKF和平滑可变结构滤波(SVSF)组合,利用EKF和SVSF分别完成电池参数辨识和SOC估计任务,相比于单一EKF电池SOC估计精度获得了提升;文献[47 ]利用两层UKF互相嵌套的方式,形成双层架构解决单一UKF在高阶非线性系统估计精度低的问题;文献[48 ]提出考虑电池寿命衰退影响的卡尔曼滤波并行结构,完成电池SOC估计及修正;文献[42 ]为了弥补卡尔曼滤波鲁棒性差以及H无穷滤波依赖初值的问题,提出一种两者联合SOC估计方式,保证SOC估计误差被可靠地限制在2%以内. ...
1
... 由于经典卡尔曼滤波算法仅适用于线性定常系统,而锂电池电化学过程表现为非线性、时变等复杂特点,经典卡尔曼滤波算法难以形成有效估计.因此,专家学者们围绕非线性系统下的状态估计问题对KF算法进行了多种改进,使其更适用于锂电池SOC估计应用.例如,文献[35 -36 ]借助泰勒级数展开对非线性系统线性化得到的拓展卡尔曼(extended kalman filter,EKF)滤波算法形成对锂电池SOC的准确观测,有效地将适用于线性系统的KF拓展至非线性系统之中;文献[37 -38 ]通过引入无迹变换,避免了非线性系统在泰勒级数展开时导致的估计精度损失,形成了锂电池SOC的无迹卡尔曼(unscented kalman filter,UKF)估计模型,获得了更为优异的估计精度;文献[39 ]提出容积卡尔曼滤波(cubature kalman filter,CKF)模型的锂电池SOC估计方式,克服了UKF在高维情况下滤波精度不高的问题.与此同时,部分研究者将自适应思想引入卡尔曼算法中,解决锂电池参数变化和外界干扰对估计精度的影响.如文献[40 -42 ]在EKF和UKF计算中加入了参数辨识步骤,形成了自适应卡尔曼(adaptive kalman filter,AKF)算法,可以实时响应电池参数变化导致SOC估计误差;文献[43 ]将在EKF中加入了模糊调节步骤,更为准确地 修正了外界噪声的变化对电池SOC估计的影响.除了上述解决锂电池非线性和参数时变特点以外的改进,为了拓展卡尔曼算法在锂电池状态估计中的应用范围,文献[44 -45 ]建立了双卡尔曼体系下的电池SOC观测模型,利用KF准确描述电池参数变化,同时辅助EKF估计电池SOC.表5 对比出了多种不同卡尔曼滤波及改进算法具有不同的优缺点. ...
1
... 由于经典卡尔曼滤波算法仅适用于线性定常系统,而锂电池电化学过程表现为非线性、时变等复杂特点,经典卡尔曼滤波算法难以形成有效估计.因此,专家学者们围绕非线性系统下的状态估计问题对KF算法进行了多种改进,使其更适用于锂电池SOC估计应用.例如,文献[35 -36 ]借助泰勒级数展开对非线性系统线性化得到的拓展卡尔曼(extended kalman filter,EKF)滤波算法形成对锂电池SOC的准确观测,有效地将适用于线性系统的KF拓展至非线性系统之中;文献[37 -38 ]通过引入无迹变换,避免了非线性系统在泰勒级数展开时导致的估计精度损失,形成了锂电池SOC的无迹卡尔曼(unscented kalman filter,UKF)估计模型,获得了更为优异的估计精度;文献[39 ]提出容积卡尔曼滤波(cubature kalman filter,CKF)模型的锂电池SOC估计方式,克服了UKF在高维情况下滤波精度不高的问题.与此同时,部分研究者将自适应思想引入卡尔曼算法中,解决锂电池参数变化和外界干扰对估计精度的影响.如文献[40 -42 ]在EKF和UKF计算中加入了参数辨识步骤,形成了自适应卡尔曼(adaptive kalman filter,AKF)算法,可以实时响应电池参数变化导致SOC估计误差;文献[43 ]将在EKF中加入了模糊调节步骤,更为准确地 修正了外界噪声的变化对电池SOC估计的影响.除了上述解决锂电池非线性和参数时变特点以外的改进,为了拓展卡尔曼算法在锂电池状态估计中的应用范围,文献[44 -45 ]建立了双卡尔曼体系下的电池SOC观测模型,利用KF准确描述电池参数变化,同时辅助EKF估计电池SOC.表5 对比出了多种不同卡尔曼滤波及改进算法具有不同的优缺点. ...
1
... 由于经典卡尔曼滤波算法仅适用于线性定常系统,而锂电池电化学过程表现为非线性、时变等复杂特点,经典卡尔曼滤波算法难以形成有效估计.因此,专家学者们围绕非线性系统下的状态估计问题对KF算法进行了多种改进,使其更适用于锂电池SOC估计应用.例如,文献[35 -36 ]借助泰勒级数展开对非线性系统线性化得到的拓展卡尔曼(extended kalman filter,EKF)滤波算法形成对锂电池SOC的准确观测,有效地将适用于线性系统的KF拓展至非线性系统之中;文献[37 -38 ]通过引入无迹变换,避免了非线性系统在泰勒级数展开时导致的估计精度损失,形成了锂电池SOC的无迹卡尔曼(unscented kalman filter,UKF)估计模型,获得了更为优异的估计精度;文献[39 ]提出容积卡尔曼滤波(cubature kalman filter,CKF)模型的锂电池SOC估计方式,克服了UKF在高维情况下滤波精度不高的问题.与此同时,部分研究者将自适应思想引入卡尔曼算法中,解决锂电池参数变化和外界干扰对估计精度的影响.如文献[40 -42 ]在EKF和UKF计算中加入了参数辨识步骤,形成了自适应卡尔曼(adaptive kalman filter,AKF)算法,可以实时响应电池参数变化导致SOC估计误差;文献[43 ]将在EKF中加入了模糊调节步骤,更为准确地 修正了外界噪声的变化对电池SOC估计的影响.除了上述解决锂电池非线性和参数时变特点以外的改进,为了拓展卡尔曼算法在锂电池状态估计中的应用范围,文献[44 -45 ]建立了双卡尔曼体系下的电池SOC观测模型,利用KF准确描述电池参数变化,同时辅助EKF估计电池SOC.表5 对比出了多种不同卡尔曼滤波及改进算法具有不同的优缺点. ...
1
... 由于经典卡尔曼滤波算法仅适用于线性定常系统,而锂电池电化学过程表现为非线性、时变等复杂特点,经典卡尔曼滤波算法难以形成有效估计.因此,专家学者们围绕非线性系统下的状态估计问题对KF算法进行了多种改进,使其更适用于锂电池SOC估计应用.例如,文献[35 -36 ]借助泰勒级数展开对非线性系统线性化得到的拓展卡尔曼(extended kalman filter,EKF)滤波算法形成对锂电池SOC的准确观测,有效地将适用于线性系统的KF拓展至非线性系统之中;文献[37 -38 ]通过引入无迹变换,避免了非线性系统在泰勒级数展开时导致的估计精度损失,形成了锂电池SOC的无迹卡尔曼(unscented kalman filter,UKF)估计模型,获得了更为优异的估计精度;文献[39 ]提出容积卡尔曼滤波(cubature kalman filter,CKF)模型的锂电池SOC估计方式,克服了UKF在高维情况下滤波精度不高的问题.与此同时,部分研究者将自适应思想引入卡尔曼算法中,解决锂电池参数变化和外界干扰对估计精度的影响.如文献[40 -42 ]在EKF和UKF计算中加入了参数辨识步骤,形成了自适应卡尔曼(adaptive kalman filter,AKF)算法,可以实时响应电池参数变化导致SOC估计误差;文献[43 ]将在EKF中加入了模糊调节步骤,更为准确地 修正了外界噪声的变化对电池SOC估计的影响.除了上述解决锂电池非线性和参数时变特点以外的改进,为了拓展卡尔曼算法在锂电池状态估计中的应用范围,文献[44 -45 ]建立了双卡尔曼体系下的电池SOC观测模型,利用KF准确描述电池参数变化,同时辅助EKF估计电池SOC.表5 对比出了多种不同卡尔曼滤波及改进算法具有不同的优缺点. ...
1
... 由于经典卡尔曼滤波算法仅适用于线性定常系统,而锂电池电化学过程表现为非线性、时变等复杂特点,经典卡尔曼滤波算法难以形成有效估计.因此,专家学者们围绕非线性系统下的状态估计问题对KF算法进行了多种改进,使其更适用于锂电池SOC估计应用.例如,文献[35 -36 ]借助泰勒级数展开对非线性系统线性化得到的拓展卡尔曼(extended kalman filter,EKF)滤波算法形成对锂电池SOC的准确观测,有效地将适用于线性系统的KF拓展至非线性系统之中;文献[37 -38 ]通过引入无迹变换,避免了非线性系统在泰勒级数展开时导致的估计精度损失,形成了锂电池SOC的无迹卡尔曼(unscented kalman filter,UKF)估计模型,获得了更为优异的估计精度;文献[39 ]提出容积卡尔曼滤波(cubature kalman filter,CKF)模型的锂电池SOC估计方式,克服了UKF在高维情况下滤波精度不高的问题.与此同时,部分研究者将自适应思想引入卡尔曼算法中,解决锂电池参数变化和外界干扰对估计精度的影响.如文献[40 -42 ]在EKF和UKF计算中加入了参数辨识步骤,形成了自适应卡尔曼(adaptive kalman filter,AKF)算法,可以实时响应电池参数变化导致SOC估计误差;文献[43 ]将在EKF中加入了模糊调节步骤,更为准确地 修正了外界噪声的变化对电池SOC估计的影响.除了上述解决锂电池非线性和参数时变特点以外的改进,为了拓展卡尔曼算法在锂电池状态估计中的应用范围,文献[44 -45 ]建立了双卡尔曼体系下的电池SOC观测模型,利用KF准确描述电池参数变化,同时辅助EKF估计电池SOC.表5 对比出了多种不同卡尔曼滤波及改进算法具有不同的优缺点. ...
1
... 由于经典卡尔曼滤波算法仅适用于线性定常系统,而锂电池电化学过程表现为非线性、时变等复杂特点,经典卡尔曼滤波算法难以形成有效估计.因此,专家学者们围绕非线性系统下的状态估计问题对KF算法进行了多种改进,使其更适用于锂电池SOC估计应用.例如,文献[35 -36 ]借助泰勒级数展开对非线性系统线性化得到的拓展卡尔曼(extended kalman filter,EKF)滤波算法形成对锂电池SOC的准确观测,有效地将适用于线性系统的KF拓展至非线性系统之中;文献[37 -38 ]通过引入无迹变换,避免了非线性系统在泰勒级数展开时导致的估计精度损失,形成了锂电池SOC的无迹卡尔曼(unscented kalman filter,UKF)估计模型,获得了更为优异的估计精度;文献[39 ]提出容积卡尔曼滤波(cubature kalman filter,CKF)模型的锂电池SOC估计方式,克服了UKF在高维情况下滤波精度不高的问题.与此同时,部分研究者将自适应思想引入卡尔曼算法中,解决锂电池参数变化和外界干扰对估计精度的影响.如文献[40 -42 ]在EKF和UKF计算中加入了参数辨识步骤,形成了自适应卡尔曼(adaptive kalman filter,AKF)算法,可以实时响应电池参数变化导致SOC估计误差;文献[43 ]将在EKF中加入了模糊调节步骤,更为准确地 修正了外界噪声的变化对电池SOC估计的影响.除了上述解决锂电池非线性和参数时变特点以外的改进,为了拓展卡尔曼算法在锂电池状态估计中的应用范围,文献[44 -45 ]建立了双卡尔曼体系下的电池SOC观测模型,利用KF准确描述电池参数变化,同时辅助EKF估计电池SOC.表5 对比出了多种不同卡尔曼滤波及改进算法具有不同的优缺点. ...
1
... 除了上述单独对卡尔曼估计算法改进以外,部分研究者提出适当组合电池SOC卡尔曼类估计模型以达到更佳的估计精度.如文献[46 ]将EKF和平滑可变结构滤波(SVSF)组合,利用EKF和SVSF分别完成电池参数辨识和SOC估计任务,相比于单一EKF电池SOC估计精度获得了提升;文献[47 ]利用两层UKF互相嵌套的方式,形成双层架构解决单一UKF在高阶非线性系统估计精度低的问题;文献[48 ]提出考虑电池寿命衰退影响的卡尔曼滤波并行结构,完成电池SOC估计及修正;文献[42 ]为了弥补卡尔曼滤波鲁棒性差以及H无穷滤波依赖初值的问题,提出一种两者联合SOC估计方式,保证SOC估计误差被可靠地限制在2%以内. ...
1
... 除了上述单独对卡尔曼估计算法改进以外,部分研究者提出适当组合电池SOC卡尔曼类估计模型以达到更佳的估计精度.如文献[46 ]将EKF和平滑可变结构滤波(SVSF)组合,利用EKF和SVSF分别完成电池参数辨识和SOC估计任务,相比于单一EKF电池SOC估计精度获得了提升;文献[47 ]利用两层UKF互相嵌套的方式,形成双层架构解决单一UKF在高阶非线性系统估计精度低的问题;文献[48 ]提出考虑电池寿命衰退影响的卡尔曼滤波并行结构,完成电池SOC估计及修正;文献[42 ]为了弥补卡尔曼滤波鲁棒性差以及H无穷滤波依赖初值的问题,提出一种两者联合SOC估计方式,保证SOC估计误差被可靠地限制在2%以内. ...
1
... 除了上述单独对卡尔曼估计算法改进以外,部分研究者提出适当组合电池SOC卡尔曼类估计模型以达到更佳的估计精度.如文献[46 ]将EKF和平滑可变结构滤波(SVSF)组合,利用EKF和SVSF分别完成电池参数辨识和SOC估计任务,相比于单一EKF电池SOC估计精度获得了提升;文献[47 ]利用两层UKF互相嵌套的方式,形成双层架构解决单一UKF在高阶非线性系统估计精度低的问题;文献[48 ]提出考虑电池寿命衰退影响的卡尔曼滤波并行结构,完成电池SOC估计及修正;文献[42 ]为了弥补卡尔曼滤波鲁棒性差以及H无穷滤波依赖初值的问题,提出一种两者联合SOC估计方式,保证SOC估计误差被可靠地限制在2%以内. ...
1
... 除了上述单独对卡尔曼估计算法改进以外,部分研究者提出适当组合电池SOC卡尔曼类估计模型以达到更佳的估计精度.如文献[46 ]将EKF和平滑可变结构滤波(SVSF)组合,利用EKF和SVSF分别完成电池参数辨识和SOC估计任务,相比于单一EKF电池SOC估计精度获得了提升;文献[47 ]利用两层UKF互相嵌套的方式,形成双层架构解决单一UKF在高阶非线性系统估计精度低的问题;文献[48 ]提出考虑电池寿命衰退影响的卡尔曼滤波并行结构,完成电池SOC估计及修正;文献[42 ]为了弥补卡尔曼滤波鲁棒性差以及H无穷滤波依赖初值的问题,提出一种两者联合SOC估计方式,保证SOC估计误差被可靠地限制在2%以内. ...
1
... 除了上述单独对卡尔曼估计算法改进以外,部分研究者提出适当组合电池SOC卡尔曼类估计模型以达到更佳的估计精度.如文献[46 ]将EKF和平滑可变结构滤波(SVSF)组合,利用EKF和SVSF分别完成电池参数辨识和SOC估计任务,相比于单一EKF电池SOC估计精度获得了提升;文献[47 ]利用两层UKF互相嵌套的方式,形成双层架构解决单一UKF在高阶非线性系统估计精度低的问题;文献[48 ]提出考虑电池寿命衰退影响的卡尔曼滤波并行结构,完成电池SOC估计及修正;文献[42 ]为了弥补卡尔曼滤波鲁棒性差以及H无穷滤波依赖初值的问题,提出一种两者联合SOC估计方式,保证SOC估计误差被可靠地限制在2%以内. ...
1
... 除了上述单独对卡尔曼估计算法改进以外,部分研究者提出适当组合电池SOC卡尔曼类估计模型以达到更佳的估计精度.如文献[46 ]将EKF和平滑可变结构滤波(SVSF)组合,利用EKF和SVSF分别完成电池参数辨识和SOC估计任务,相比于单一EKF电池SOC估计精度获得了提升;文献[47 ]利用两层UKF互相嵌套的方式,形成双层架构解决单一UKF在高阶非线性系统估计精度低的问题;文献[48 ]提出考虑电池寿命衰退影响的卡尔曼滤波并行结构,完成电池SOC估计及修正;文献[42 ]为了弥补卡尔曼滤波鲁棒性差以及H无穷滤波依赖初值的问题,提出一种两者联合SOC估计方式,保证SOC估计误差被可靠地限制在2%以内. ...
1
... 粒子滤波是一种利用蒙特卡洛方法递推的贝叶斯滤波[49 ] .相比于卡尔曼类滤波算法,其主要不同之处在于通过蒙特卡洛方法消除系统噪声必须为高斯噪声的假设条件,因此适用于非线性非高斯的复杂系统状态估计.在锂电池SOC估计应用中,假设电池SOC初始状态概率密度函数已知p (C s o c ( 0 ) ) ,通过贝叶斯估计的状态值C s o c ( k ) U ( k ) 递归计算出状态值C s o c ( k ) p (C s o c ( k ) U (1∶ k ) ),贝叶斯递归估计关系计算如公式(8 )~(9 )所示. ...
1
... 粒子滤波是一种利用蒙特卡洛方法递推的贝叶斯滤波[49 ] .相比于卡尔曼类滤波算法,其主要不同之处在于通过蒙特卡洛方法消除系统噪声必须为高斯噪声的假设条件,因此适用于非线性非高斯的复杂系统状态估计.在锂电池SOC估计应用中,假设电池SOC初始状态概率密度函数已知p (C s o c ( 0 ) ) ,通过贝叶斯估计的状态值C s o c ( k ) U ( k ) 递归计算出状态值C s o c ( k ) p (C s o c ( k ) U (1∶ k ) ),贝叶斯递归估计关系计算如公式(8 )~(9 )所示. ...
2
... 尽管常规粒子滤波算法克服了卡尔曼滤波架构对系统高斯噪声的假设,也解决了贝叶斯递归估计中积分无法计算的等效操作,但是在实际应用中粒子滤波仍存在局限性.为此,研究者通过借鉴卡尔曼类滤波体系和引入优化算法,提升了粒子滤波算法性能,避免了粒子贫化现象,如文献[50 ]提出扩展粒子滤波和无迹粒子滤波避免传统粒子滤波存在的粒子退化现象,可以准确表示出锂电池SOC的实际后验概率分布,提高估计精度;而文献[51 ]是通过一种权重选择方式改进粒子滤波算法,避免了粒子退化现象;文献[52 ]提出改进狼群的粒子滤波算法,利用灰狼表示粒子,不断更新狼群位置实现对真实概率分布的拟合,控制电池SOC估计误差在1%以内. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
2
... 尽管常规粒子滤波算法克服了卡尔曼滤波架构对系统高斯噪声的假设,也解决了贝叶斯递归估计中积分无法计算的等效操作,但是在实际应用中粒子滤波仍存在局限性.为此,研究者通过借鉴卡尔曼类滤波体系和引入优化算法,提升了粒子滤波算法性能,避免了粒子贫化现象,如文献[50 ]提出扩展粒子滤波和无迹粒子滤波避免传统粒子滤波存在的粒子退化现象,可以准确表示出锂电池SOC的实际后验概率分布,提高估计精度;而文献[51 ]是通过一种权重选择方式改进粒子滤波算法,避免了粒子退化现象;文献[52 ]提出改进狼群的粒子滤波算法,利用灰狼表示粒子,不断更新狼群位置实现对真实概率分布的拟合,控制电池SOC估计误差在1%以内. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
1
... 尽管常规粒子滤波算法克服了卡尔曼滤波架构对系统高斯噪声的假设,也解决了贝叶斯递归估计中积分无法计算的等效操作,但是在实际应用中粒子滤波仍存在局限性.为此,研究者通过借鉴卡尔曼类滤波体系和引入优化算法,提升了粒子滤波算法性能,避免了粒子贫化现象,如文献[50 ]提出扩展粒子滤波和无迹粒子滤波避免传统粒子滤波存在的粒子退化现象,可以准确表示出锂电池SOC的实际后验概率分布,提高估计精度;而文献[51 ]是通过一种权重选择方式改进粒子滤波算法,避免了粒子退化现象;文献[52 ]提出改进狼群的粒子滤波算法,利用灰狼表示粒子,不断更新狼群位置实现对真实概率分布的拟合,控制电池SOC估计误差在1%以内. ...
1
... 尽管常规粒子滤波算法克服了卡尔曼滤波架构对系统高斯噪声的假设,也解决了贝叶斯递归估计中积分无法计算的等效操作,但是在实际应用中粒子滤波仍存在局限性.为此,研究者通过借鉴卡尔曼类滤波体系和引入优化算法,提升了粒子滤波算法性能,避免了粒子贫化现象,如文献[50 ]提出扩展粒子滤波和无迹粒子滤波避免传统粒子滤波存在的粒子退化现象,可以准确表示出锂电池SOC的实际后验概率分布,提高估计精度;而文献[51 ]是通过一种权重选择方式改进粒子滤波算法,避免了粒子退化现象;文献[52 ]提出改进狼群的粒子滤波算法,利用灰狼表示粒子,不断更新狼群位置实现对真实概率分布的拟合,控制电池SOC估计误差在1%以内. ...
2
... 尽管常规粒子滤波算法克服了卡尔曼滤波架构对系统高斯噪声的假设,也解决了贝叶斯递归估计中积分无法计算的等效操作,但是在实际应用中粒子滤波仍存在局限性.为此,研究者通过借鉴卡尔曼类滤波体系和引入优化算法,提升了粒子滤波算法性能,避免了粒子贫化现象,如文献[50 ]提出扩展粒子滤波和无迹粒子滤波避免传统粒子滤波存在的粒子退化现象,可以准确表示出锂电池SOC的实际后验概率分布,提高估计精度;而文献[51 ]是通过一种权重选择方式改进粒子滤波算法,避免了粒子退化现象;文献[52 ]提出改进狼群的粒子滤波算法,利用灰狼表示粒子,不断更新狼群位置实现对真实概率分布的拟合,控制电池SOC估计误差在1%以内. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
2
... 尽管常规粒子滤波算法克服了卡尔曼滤波架构对系统高斯噪声的假设,也解决了贝叶斯递归估计中积分无法计算的等效操作,但是在实际应用中粒子滤波仍存在局限性.为此,研究者通过借鉴卡尔曼类滤波体系和引入优化算法,提升了粒子滤波算法性能,避免了粒子贫化现象,如文献[50 ]提出扩展粒子滤波和无迹粒子滤波避免传统粒子滤波存在的粒子退化现象,可以准确表示出锂电池SOC的实际后验概率分布,提高估计精度;而文献[51 ]是通过一种权重选择方式改进粒子滤波算法,避免了粒子退化现象;文献[52 ]提出改进狼群的粒子滤波算法,利用灰狼表示粒子,不断更新狼群位置实现对真实概率分布的拟合,控制电池SOC估计误差在1%以内. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
2
... 通过对公式(12) 的求解可以获得目标函数J <1/θ 的递推关系,获得H∞滤波器.针对传统H∞滤波对状态和模型不确定性的突变不敏感问题,文献[53 ]通过引入次优衰落因子,提高了锂电池SOC估计的稳定性;文献[10 ]将电池温度作为系统扰动变量,运用线性矩阵不等式技术设计出鲁棒H∞滤波器,较大程度地抑制了温度扰动对电池SOC估计的影响;文献[54 ]提出基于递归最小二次整定锂电池参数后,利用自适应H∞滤波进行锂电池容量估计,其实现过程如图4 所示,克服了电池SOC初始参数和测量误差对SOC估计精度的不利影响.文献[55 ]参考粒子滤波权重更迭思想,提出具有加权新息的H∞滤波算法,以时间重要性分配不同的新息权重,提高了电池SOC估计的准确性. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
2
... 通过对公式(12) 的求解可以获得目标函数J <1/θ 的递推关系,获得H∞滤波器.针对传统H∞滤波对状态和模型不确定性的突变不敏感问题,文献[53 ]通过引入次优衰落因子,提高了锂电池SOC估计的稳定性;文献[10 ]将电池温度作为系统扰动变量,运用线性矩阵不等式技术设计出鲁棒H∞滤波器,较大程度地抑制了温度扰动对电池SOC估计的影响;文献[54 ]提出基于递归最小二次整定锂电池参数后,利用自适应H∞滤波进行锂电池容量估计,其实现过程如图4 所示,克服了电池SOC初始参数和测量误差对SOC估计精度的不利影响.文献[55 ]参考粒子滤波权重更迭思想,提出具有加权新息的H∞滤波算法,以时间重要性分配不同的新息权重,提高了电池SOC估计的准确性. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
2
... 通过对公式(12) 的求解可以获得目标函数J <1/θ 的递推关系,获得H∞滤波器.针对传统H∞滤波对状态和模型不确定性的突变不敏感问题,文献[53 ]通过引入次优衰落因子,提高了锂电池SOC估计的稳定性;文献[10 ]将电池温度作为系统扰动变量,运用线性矩阵不等式技术设计出鲁棒H∞滤波器,较大程度地抑制了温度扰动对电池SOC估计的影响;文献[54 ]提出基于递归最小二次整定锂电池参数后,利用自适应H∞滤波进行锂电池容量估计,其实现过程如图4 所示,克服了电池SOC初始参数和测量误差对SOC估计精度的不利影响.文献[55 ]参考粒子滤波权重更迭思想,提出具有加权新息的H∞滤波算法,以时间重要性分配不同的新息权重,提高了电池SOC估计的准确性. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
1
... 通过对公式(12) 的求解可以获得目标函数J <1/θ 的递推关系,获得H∞滤波器.针对传统H∞滤波对状态和模型不确定性的突变不敏感问题,文献[53 ]通过引入次优衰落因子,提高了锂电池SOC估计的稳定性;文献[10 ]将电池温度作为系统扰动变量,运用线性矩阵不等式技术设计出鲁棒H∞滤波器,较大程度地抑制了温度扰动对电池SOC估计的影响;文献[54 ]提出基于递归最小二次整定锂电池参数后,利用自适应H∞滤波进行锂电池容量估计,其实现过程如图4 所示,克服了电池SOC初始参数和测量误差对SOC估计精度的不利影响.文献[55 ]参考粒子滤波权重更迭思想,提出具有加权新息的H∞滤波算法,以时间重要性分配不同的新息权重,提高了电池SOC估计的准确性. ...
1
... 通过对公式(12) 的求解可以获得目标函数J <1/θ 的递推关系,获得H∞滤波器.针对传统H∞滤波对状态和模型不确定性的突变不敏感问题,文献[53 ]通过引入次优衰落因子,提高了锂电池SOC估计的稳定性;文献[10 ]将电池温度作为系统扰动变量,运用线性矩阵不等式技术设计出鲁棒H∞滤波器,较大程度地抑制了温度扰动对电池SOC估计的影响;文献[54 ]提出基于递归最小二次整定锂电池参数后,利用自适应H∞滤波进行锂电池容量估计,其实现过程如图4 所示,克服了电池SOC初始参数和测量误差对SOC估计精度的不利影响.文献[55 ]参考粒子滤波权重更迭思想,提出具有加权新息的H∞滤波算法,以时间重要性分配不同的新息权重,提高了电池SOC估计的准确性. ...
2
... 基于锂电池模型的SOC估计方法具有估计快速、设计过程科学严谨等优势,但锂电池等效建模精度决定了估计准确性.而锂电池具有复杂的电化学过程,数学等效的误差难以消除,且在应用过程中物性参数具有时变性,也带来了较大的模型误差.研究人员发现基于锂电池模型的SOC估计忽视了电池运行数据隐含的电池性能演变规律,而基于测量数据本身特性下的回归分析模型可以较好地完成数据特征至SOC的映射关系,将其应用于锂电池SOC估计之中,可以取得良好的估计效果[56 ] .图5 展示了基于数据驱动的机器学习算法估计锂电池SOC的流程和各环节中的主要技术要点. ...
... 随着不同类型神经网络形式被提出,研究者将其分别应用于锂电池SOC估计中,以达到更高的估计精度.如文献[57 ]和[58]提出应用小型神经网络和极限学习机模型预测锂电池SOC,不同于传统极限学习机(extreme learning machine,ELM),通过引入核技术和狼群优化算法,增强了模型的非线性映射能力和预测精度;文献[56 ]和[59]以经典误差反向传播神经网络(backpropagation neural network,BPNN)模型为SOC预测模型,通过引入遗传算法和蝗虫优化算法优化网络参数,建立高精度的锂电池SOC预测模型.从上述研究可以看出,采用群智能算法优化神经网络模型,避免梯度下降等传统优化算法造成局部最优问题已是当前研究的主要思路之一.此外,文献[60 ]通过建立基于核技术的径向基神经网络(radial basis function,RBF)解决锂电池SOC估计的非线性问题,并通过回溯搜索算法优化模型参数,将锂电池SOC估计误差降低在2%以内,而文献[61 ]提出广义回归神经网络(RBF神经网络的一种)实现了任一充放电状态下SOC的精确估计;文献[62 ]将模糊理论与神经网络相结合,通过设计模糊规则优化算法对网络结构进行优化,提高了电池SOC的预测精度.同时,研究者考虑锂电池SOC变化过程中的时序性,分别提出应用具有时间序列描绘特性的非线性自回归网络(nonlinear autoregressive with exogeneous inputs neural network,NARX)[63 ] 以及经典的深度学习网络(deep neural network,DNN),如长短期记忆循环神经网络(long short-term memory,LSTM)[64 ] 和门控循环神经网络(gated recurrent unit,GRU)[65 -66 ] 等模型,完成高性能的锂电池SOC估计,已取得良好的预测结果.在锂电池SOC估计的应用中,神经网络模型优势在于可以解决锂离子电池可测变量及特征与电池SOC之间复杂的非线性映射关系,模型的适应性好、精度高,但网络过大会导致模型参数大幅度增加,计算量过大,易陷入局部最优下的过/欠拟合,且对参数初始值较为敏感.表6 对比了用于锂电池SOC估计的不同神经网络优缺点. ...
2
... 基于锂电池模型的SOC估计方法具有估计快速、设计过程科学严谨等优势,但锂电池等效建模精度决定了估计准确性.而锂电池具有复杂的电化学过程,数学等效的误差难以消除,且在应用过程中物性参数具有时变性,也带来了较大的模型误差.研究人员发现基于锂电池模型的SOC估计忽视了电池运行数据隐含的电池性能演变规律,而基于测量数据本身特性下的回归分析模型可以较好地完成数据特征至SOC的映射关系,将其应用于锂电池SOC估计之中,可以取得良好的估计效果[56 ] .图5 展示了基于数据驱动的机器学习算法估计锂电池SOC的流程和各环节中的主要技术要点. ...
... 随着不同类型神经网络形式被提出,研究者将其分别应用于锂电池SOC估计中,以达到更高的估计精度.如文献[57 ]和[58]提出应用小型神经网络和极限学习机模型预测锂电池SOC,不同于传统极限学习机(extreme learning machine,ELM),通过引入核技术和狼群优化算法,增强了模型的非线性映射能力和预测精度;文献[56 ]和[59]以经典误差反向传播神经网络(backpropagation neural network,BPNN)模型为SOC预测模型,通过引入遗传算法和蝗虫优化算法优化网络参数,建立高精度的锂电池SOC预测模型.从上述研究可以看出,采用群智能算法优化神经网络模型,避免梯度下降等传统优化算法造成局部最优问题已是当前研究的主要思路之一.此外,文献[60 ]通过建立基于核技术的径向基神经网络(radial basis function,RBF)解决锂电池SOC估计的非线性问题,并通过回溯搜索算法优化模型参数,将锂电池SOC估计误差降低在2%以内,而文献[61 ]提出广义回归神经网络(RBF神经网络的一种)实现了任一充放电状态下SOC的精确估计;文献[62 ]将模糊理论与神经网络相结合,通过设计模糊规则优化算法对网络结构进行优化,提高了电池SOC的预测精度.同时,研究者考虑锂电池SOC变化过程中的时序性,分别提出应用具有时间序列描绘特性的非线性自回归网络(nonlinear autoregressive with exogeneous inputs neural network,NARX)[63 ] 以及经典的深度学习网络(deep neural network,DNN),如长短期记忆循环神经网络(long short-term memory,LSTM)[64 ] 和门控循环神经网络(gated recurrent unit,GRU)[65 -66 ] 等模型,完成高性能的锂电池SOC估计,已取得良好的预测结果.在锂电池SOC估计的应用中,神经网络模型优势在于可以解决锂离子电池可测变量及特征与电池SOC之间复杂的非线性映射关系,模型的适应性好、精度高,但网络过大会导致模型参数大幅度增加,计算量过大,易陷入局部最优下的过/欠拟合,且对参数初始值较为敏感.表6 对比了用于锂电池SOC估计的不同神经网络优缺点. ...
2
... 随着不同类型神经网络形式被提出,研究者将其分别应用于锂电池SOC估计中,以达到更高的估计精度.如文献[57 ]和[58]提出应用小型神经网络和极限学习机模型预测锂电池SOC,不同于传统极限学习机(extreme learning machine,ELM),通过引入核技术和狼群优化算法,增强了模型的非线性映射能力和预测精度;文献[56 ]和[59]以经典误差反向传播神经网络(backpropagation neural network,BPNN)模型为SOC预测模型,通过引入遗传算法和蝗虫优化算法优化网络参数,建立高精度的锂电池SOC预测模型.从上述研究可以看出,采用群智能算法优化神经网络模型,避免梯度下降等传统优化算法造成局部最优问题已是当前研究的主要思路之一.此外,文献[60 ]通过建立基于核技术的径向基神经网络(radial basis function,RBF)解决锂电池SOC估计的非线性问题,并通过回溯搜索算法优化模型参数,将锂电池SOC估计误差降低在2%以内,而文献[61 ]提出广义回归神经网络(RBF神经网络的一种)实现了任一充放电状态下SOC的精确估计;文献[62 ]将模糊理论与神经网络相结合,通过设计模糊规则优化算法对网络结构进行优化,提高了电池SOC的预测精度.同时,研究者考虑锂电池SOC变化过程中的时序性,分别提出应用具有时间序列描绘特性的非线性自回归网络(nonlinear autoregressive with exogeneous inputs neural network,NARX)[63 ] 以及经典的深度学习网络(deep neural network,DNN),如长短期记忆循环神经网络(long short-term memory,LSTM)[64 ] 和门控循环神经网络(gated recurrent unit,GRU)[65 -66 ] 等模型,完成高性能的锂电池SOC估计,已取得良好的预测结果.在锂电池SOC估计的应用中,神经网络模型优势在于可以解决锂离子电池可测变量及特征与电池SOC之间复杂的非线性映射关系,模型的适应性好、精度高,但网络过大会导致模型参数大幅度增加,计算量过大,易陷入局部最优下的过/欠拟合,且对参数初始值较为敏感.表6 对比了用于锂电池SOC估计的不同神经网络优缺点. ...
... Neural network technology for lithium battery SOC estimation
Table 6 网络类型 网络模型优势 网络模型局限性 ELM[57 -58 ] 1.网络结构简单; ...
2
... 随着不同类型神经网络形式被提出,研究者将其分别应用于锂电池SOC估计中,以达到更高的估计精度.如文献[57 ]和[58]提出应用小型神经网络和极限学习机模型预测锂电池SOC,不同于传统极限学习机(extreme learning machine,ELM),通过引入核技术和狼群优化算法,增强了模型的非线性映射能力和预测精度;文献[56 ]和[59]以经典误差反向传播神经网络(backpropagation neural network,BPNN)模型为SOC预测模型,通过引入遗传算法和蝗虫优化算法优化网络参数,建立高精度的锂电池SOC预测模型.从上述研究可以看出,采用群智能算法优化神经网络模型,避免梯度下降等传统优化算法造成局部最优问题已是当前研究的主要思路之一.此外,文献[60 ]通过建立基于核技术的径向基神经网络(radial basis function,RBF)解决锂电池SOC估计的非线性问题,并通过回溯搜索算法优化模型参数,将锂电池SOC估计误差降低在2%以内,而文献[61 ]提出广义回归神经网络(RBF神经网络的一种)实现了任一充放电状态下SOC的精确估计;文献[62 ]将模糊理论与神经网络相结合,通过设计模糊规则优化算法对网络结构进行优化,提高了电池SOC的预测精度.同时,研究者考虑锂电池SOC变化过程中的时序性,分别提出应用具有时间序列描绘特性的非线性自回归网络(nonlinear autoregressive with exogeneous inputs neural network,NARX)[63 ] 以及经典的深度学习网络(deep neural network,DNN),如长短期记忆循环神经网络(long short-term memory,LSTM)[64 ] 和门控循环神经网络(gated recurrent unit,GRU)[65 -66 ] 等模型,完成高性能的锂电池SOC估计,已取得良好的预测结果.在锂电池SOC估计的应用中,神经网络模型优势在于可以解决锂离子电池可测变量及特征与电池SOC之间复杂的非线性映射关系,模型的适应性好、精度高,但网络过大会导致模型参数大幅度增加,计算量过大,易陷入局部最优下的过/欠拟合,且对参数初始值较为敏感.表6 对比了用于锂电池SOC估计的不同神经网络优缺点. ...
... Neural network technology for lithium battery SOC estimation
Table 6 网络类型 网络模型优势 网络模型局限性 ELM[57 -58 ] 1.网络结构简单; ...
1
... Neural network technology for lithium battery SOC estimation
Table 6 网络类型 网络模型优势 网络模型局限性 ELM[57 -58 ] 1.网络结构简单; ...
1
... Neural network technology for lithium battery SOC estimation
Table 6 网络类型 网络模型优势 网络模型局限性 ELM[57 -58 ] 1.网络结构简单; ...
BPNN[59 ] 1.可以满足锂电池SOC估计的非线性映射关系; ...
BPNN[59 ] 1.可以满足锂电池SOC估计的非线性映射关系; ...
2
... 随着不同类型神经网络形式被提出,研究者将其分别应用于锂电池SOC估计中,以达到更高的估计精度.如文献[57 ]和[58]提出应用小型神经网络和极限学习机模型预测锂电池SOC,不同于传统极限学习机(extreme learning machine,ELM),通过引入核技术和狼群优化算法,增强了模型的非线性映射能力和预测精度;文献[56 ]和[59]以经典误差反向传播神经网络(backpropagation neural network,BPNN)模型为SOC预测模型,通过引入遗传算法和蝗虫优化算法优化网络参数,建立高精度的锂电池SOC预测模型.从上述研究可以看出,采用群智能算法优化神经网络模型,避免梯度下降等传统优化算法造成局部最优问题已是当前研究的主要思路之一.此外,文献[60 ]通过建立基于核技术的径向基神经网络(radial basis function,RBF)解决锂电池SOC估计的非线性问题,并通过回溯搜索算法优化模型参数,将锂电池SOC估计误差降低在2%以内,而文献[61 ]提出广义回归神经网络(RBF神经网络的一种)实现了任一充放电状态下SOC的精确估计;文献[62 ]将模糊理论与神经网络相结合,通过设计模糊规则优化算法对网络结构进行优化,提高了电池SOC的预测精度.同时,研究者考虑锂电池SOC变化过程中的时序性,分别提出应用具有时间序列描绘特性的非线性自回归网络(nonlinear autoregressive with exogeneous inputs neural network,NARX)[63 ] 以及经典的深度学习网络(deep neural network,DNN),如长短期记忆循环神经网络(long short-term memory,LSTM)[64 ] 和门控循环神经网络(gated recurrent unit,GRU)[65 -66 ] 等模型,完成高性能的锂电池SOC估计,已取得良好的预测结果.在锂电池SOC估计的应用中,神经网络模型优势在于可以解决锂离子电池可测变量及特征与电池SOC之间复杂的非线性映射关系,模型的适应性好、精度高,但网络过大会导致模型参数大幅度增加,计算量过大,易陷入局部最优下的过/欠拟合,且对参数初始值较为敏感.表6 对比了用于锂电池SOC估计的不同神经网络优缺点. ...
... 2.模型性能对参数的初始值敏感,易陷入局部最优值
RBF[60 ] 1.有较强的非线性映射能力,满足SOC非线性要求; ...
2
... 随着不同类型神经网络形式被提出,研究者将其分别应用于锂电池SOC估计中,以达到更高的估计精度.如文献[57 ]和[58]提出应用小型神经网络和极限学习机模型预测锂电池SOC,不同于传统极限学习机(extreme learning machine,ELM),通过引入核技术和狼群优化算法,增强了模型的非线性映射能力和预测精度;文献[56 ]和[59]以经典误差反向传播神经网络(backpropagation neural network,BPNN)模型为SOC预测模型,通过引入遗传算法和蝗虫优化算法优化网络参数,建立高精度的锂电池SOC预测模型.从上述研究可以看出,采用群智能算法优化神经网络模型,避免梯度下降等传统优化算法造成局部最优问题已是当前研究的主要思路之一.此外,文献[60 ]通过建立基于核技术的径向基神经网络(radial basis function,RBF)解决锂电池SOC估计的非线性问题,并通过回溯搜索算法优化模型参数,将锂电池SOC估计误差降低在2%以内,而文献[61 ]提出广义回归神经网络(RBF神经网络的一种)实现了任一充放电状态下SOC的精确估计;文献[62 ]将模糊理论与神经网络相结合,通过设计模糊规则优化算法对网络结构进行优化,提高了电池SOC的预测精度.同时,研究者考虑锂电池SOC变化过程中的时序性,分别提出应用具有时间序列描绘特性的非线性自回归网络(nonlinear autoregressive with exogeneous inputs neural network,NARX)[63 ] 以及经典的深度学习网络(deep neural network,DNN),如长短期记忆循环神经网络(long short-term memory,LSTM)[64 ] 和门控循环神经网络(gated recurrent unit,GRU)[65 -66 ] 等模型,完成高性能的锂电池SOC估计,已取得良好的预测结果.在锂电池SOC估计的应用中,神经网络模型优势在于可以解决锂离子电池可测变量及特征与电池SOC之间复杂的非线性映射关系,模型的适应性好、精度高,但网络过大会导致模型参数大幅度增加,计算量过大,易陷入局部最优下的过/欠拟合,且对参数初始值较为敏感.表6 对比了用于锂电池SOC估计的不同神经网络优缺点. ...
... 2.模型性能对参数的初始值敏感,易陷入局部最优值
RBF[60 ] 1.有较强的非线性映射能力,满足SOC非线性要求; ...
2
... 随着不同类型神经网络形式被提出,研究者将其分别应用于锂电池SOC估计中,以达到更高的估计精度.如文献[57 ]和[58]提出应用小型神经网络和极限学习机模型预测锂电池SOC,不同于传统极限学习机(extreme learning machine,ELM),通过引入核技术和狼群优化算法,增强了模型的非线性映射能力和预测精度;文献[56 ]和[59]以经典误差反向传播神经网络(backpropagation neural network,BPNN)模型为SOC预测模型,通过引入遗传算法和蝗虫优化算法优化网络参数,建立高精度的锂电池SOC预测模型.从上述研究可以看出,采用群智能算法优化神经网络模型,避免梯度下降等传统优化算法造成局部最优问题已是当前研究的主要思路之一.此外,文献[60 ]通过建立基于核技术的径向基神经网络(radial basis function,RBF)解决锂电池SOC估计的非线性问题,并通过回溯搜索算法优化模型参数,将锂电池SOC估计误差降低在2%以内,而文献[61 ]提出广义回归神经网络(RBF神经网络的一种)实现了任一充放电状态下SOC的精确估计;文献[62 ]将模糊理论与神经网络相结合,通过设计模糊规则优化算法对网络结构进行优化,提高了电池SOC的预测精度.同时,研究者考虑锂电池SOC变化过程中的时序性,分别提出应用具有时间序列描绘特性的非线性自回归网络(nonlinear autoregressive with exogeneous inputs neural network,NARX)[63 ] 以及经典的深度学习网络(deep neural network,DNN),如长短期记忆循环神经网络(long short-term memory,LSTM)[64 ] 和门控循环神经网络(gated recurrent unit,GRU)[65 -66 ] 等模型,完成高性能的锂电池SOC估计,已取得良好的预测结果.在锂电池SOC估计的应用中,神经网络模型优势在于可以解决锂离子电池可测变量及特征与电池SOC之间复杂的非线性映射关系,模型的适应性好、精度高,但网络过大会导致模型参数大幅度增加,计算量过大,易陷入局部最优下的过/欠拟合,且对参数初始值较为敏感.表6 对比了用于锂电池SOC估计的不同神经网络优缺点. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
2
... 随着不同类型神经网络形式被提出,研究者将其分别应用于锂电池SOC估计中,以达到更高的估计精度.如文献[57 ]和[58]提出应用小型神经网络和极限学习机模型预测锂电池SOC,不同于传统极限学习机(extreme learning machine,ELM),通过引入核技术和狼群优化算法,增强了模型的非线性映射能力和预测精度;文献[56 ]和[59]以经典误差反向传播神经网络(backpropagation neural network,BPNN)模型为SOC预测模型,通过引入遗传算法和蝗虫优化算法优化网络参数,建立高精度的锂电池SOC预测模型.从上述研究可以看出,采用群智能算法优化神经网络模型,避免梯度下降等传统优化算法造成局部最优问题已是当前研究的主要思路之一.此外,文献[60 ]通过建立基于核技术的径向基神经网络(radial basis function,RBF)解决锂电池SOC估计的非线性问题,并通过回溯搜索算法优化模型参数,将锂电池SOC估计误差降低在2%以内,而文献[61 ]提出广义回归神经网络(RBF神经网络的一种)实现了任一充放电状态下SOC的精确估计;文献[62 ]将模糊理论与神经网络相结合,通过设计模糊规则优化算法对网络结构进行优化,提高了电池SOC的预测精度.同时,研究者考虑锂电池SOC变化过程中的时序性,分别提出应用具有时间序列描绘特性的非线性自回归网络(nonlinear autoregressive with exogeneous inputs neural network,NARX)[63 ] 以及经典的深度学习网络(deep neural network,DNN),如长短期记忆循环神经网络(long short-term memory,LSTM)[64 ] 和门控循环神经网络(gated recurrent unit,GRU)[65 -66 ] 等模型,完成高性能的锂电池SOC估计,已取得良好的预测结果.在锂电池SOC估计的应用中,神经网络模型优势在于可以解决锂离子电池可测变量及特征与电池SOC之间复杂的非线性映射关系,模型的适应性好、精度高,但网络过大会导致模型参数大幅度增加,计算量过大,易陷入局部最优下的过/欠拟合,且对参数初始值较为敏感.表6 对比了用于锂电池SOC估计的不同神经网络优缺点. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
2
... 随着不同类型神经网络形式被提出,研究者将其分别应用于锂电池SOC估计中,以达到更高的估计精度.如文献[57 ]和[58]提出应用小型神经网络和极限学习机模型预测锂电池SOC,不同于传统极限学习机(extreme learning machine,ELM),通过引入核技术和狼群优化算法,增强了模型的非线性映射能力和预测精度;文献[56 ]和[59]以经典误差反向传播神经网络(backpropagation neural network,BPNN)模型为SOC预测模型,通过引入遗传算法和蝗虫优化算法优化网络参数,建立高精度的锂电池SOC预测模型.从上述研究可以看出,采用群智能算法优化神经网络模型,避免梯度下降等传统优化算法造成局部最优问题已是当前研究的主要思路之一.此外,文献[60 ]通过建立基于核技术的径向基神经网络(radial basis function,RBF)解决锂电池SOC估计的非线性问题,并通过回溯搜索算法优化模型参数,将锂电池SOC估计误差降低在2%以内,而文献[61 ]提出广义回归神经网络(RBF神经网络的一种)实现了任一充放电状态下SOC的精确估计;文献[62 ]将模糊理论与神经网络相结合,通过设计模糊规则优化算法对网络结构进行优化,提高了电池SOC的预测精度.同时,研究者考虑锂电池SOC变化过程中的时序性,分别提出应用具有时间序列描绘特性的非线性自回归网络(nonlinear autoregressive with exogeneous inputs neural network,NARX)[63 ] 以及经典的深度学习网络(deep neural network,DNN),如长短期记忆循环神经网络(long short-term memory,LSTM)[64 ] 和门控循环神经网络(gated recurrent unit,GRU)[65 -66 ] 等模型,完成高性能的锂电池SOC估计,已取得良好的预测结果.在锂电池SOC估计的应用中,神经网络模型优势在于可以解决锂离子电池可测变量及特征与电池SOC之间复杂的非线性映射关系,模型的适应性好、精度高,但网络过大会导致模型参数大幅度增加,计算量过大,易陷入局部最优下的过/欠拟合,且对参数初始值较为敏感.表6 对比了用于锂电池SOC估计的不同神经网络优缺点. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
2
... 随着不同类型神经网络形式被提出,研究者将其分别应用于锂电池SOC估计中,以达到更高的估计精度.如文献[57 ]和[58]提出应用小型神经网络和极限学习机模型预测锂电池SOC,不同于传统极限学习机(extreme learning machine,ELM),通过引入核技术和狼群优化算法,增强了模型的非线性映射能力和预测精度;文献[56 ]和[59]以经典误差反向传播神经网络(backpropagation neural network,BPNN)模型为SOC预测模型,通过引入遗传算法和蝗虫优化算法优化网络参数,建立高精度的锂电池SOC预测模型.从上述研究可以看出,采用群智能算法优化神经网络模型,避免梯度下降等传统优化算法造成局部最优问题已是当前研究的主要思路之一.此外,文献[60 ]通过建立基于核技术的径向基神经网络(radial basis function,RBF)解决锂电池SOC估计的非线性问题,并通过回溯搜索算法优化模型参数,将锂电池SOC估计误差降低在2%以内,而文献[61 ]提出广义回归神经网络(RBF神经网络的一种)实现了任一充放电状态下SOC的精确估计;文献[62 ]将模糊理论与神经网络相结合,通过设计模糊规则优化算法对网络结构进行优化,提高了电池SOC的预测精度.同时,研究者考虑锂电池SOC变化过程中的时序性,分别提出应用具有时间序列描绘特性的非线性自回归网络(nonlinear autoregressive with exogeneous inputs neural network,NARX)[63 ] 以及经典的深度学习网络(deep neural network,DNN),如长短期记忆循环神经网络(long short-term memory,LSTM)[64 ] 和门控循环神经网络(gated recurrent unit,GRU)[65 -66 ] 等模型,完成高性能的锂电池SOC估计,已取得良好的预测结果.在锂电池SOC估计的应用中,神经网络模型优势在于可以解决锂离子电池可测变量及特征与电池SOC之间复杂的非线性映射关系,模型的适应性好、精度高,但网络过大会导致模型参数大幅度增加,计算量过大,易陷入局部最优下的过/欠拟合,且对参数初始值较为敏感.表6 对比了用于锂电池SOC估计的不同神经网络优缺点. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
2
... 随着不同类型神经网络形式被提出,研究者将其分别应用于锂电池SOC估计中,以达到更高的估计精度.如文献[57 ]和[58]提出应用小型神经网络和极限学习机模型预测锂电池SOC,不同于传统极限学习机(extreme learning machine,ELM),通过引入核技术和狼群优化算法,增强了模型的非线性映射能力和预测精度;文献[56 ]和[59]以经典误差反向传播神经网络(backpropagation neural network,BPNN)模型为SOC预测模型,通过引入遗传算法和蝗虫优化算法优化网络参数,建立高精度的锂电池SOC预测模型.从上述研究可以看出,采用群智能算法优化神经网络模型,避免梯度下降等传统优化算法造成局部最优问题已是当前研究的主要思路之一.此外,文献[60 ]通过建立基于核技术的径向基神经网络(radial basis function,RBF)解决锂电池SOC估计的非线性问题,并通过回溯搜索算法优化模型参数,将锂电池SOC估计误差降低在2%以内,而文献[61 ]提出广义回归神经网络(RBF神经网络的一种)实现了任一充放电状态下SOC的精确估计;文献[62 ]将模糊理论与神经网络相结合,通过设计模糊规则优化算法对网络结构进行优化,提高了电池SOC的预测精度.同时,研究者考虑锂电池SOC变化过程中的时序性,分别提出应用具有时间序列描绘特性的非线性自回归网络(nonlinear autoregressive with exogeneous inputs neural network,NARX)[63 ] 以及经典的深度学习网络(deep neural network,DNN),如长短期记忆循环神经网络(long short-term memory,LSTM)[64 ] 和门控循环神经网络(gated recurrent unit,GRU)[65 -66 ] 等模型,完成高性能的锂电池SOC估计,已取得良好的预测结果.在锂电池SOC估计的应用中,神经网络模型优势在于可以解决锂离子电池可测变量及特征与电池SOC之间复杂的非线性映射关系,模型的适应性好、精度高,但网络过大会导致模型参数大幅度增加,计算量过大,易陷入局部最优下的过/欠拟合,且对参数初始值较为敏感.表6 对比了用于锂电池SOC估计的不同神经网络优缺点. ...
... 3. 算法的计算复杂度高
NARX[63 ] 1.具有时间序列分析能力; ...
2
... 随着不同类型神经网络形式被提出,研究者将其分别应用于锂电池SOC估计中,以达到更高的估计精度.如文献[57 ]和[58]提出应用小型神经网络和极限学习机模型预测锂电池SOC,不同于传统极限学习机(extreme learning machine,ELM),通过引入核技术和狼群优化算法,增强了模型的非线性映射能力和预测精度;文献[56 ]和[59]以经典误差反向传播神经网络(backpropagation neural network,BPNN)模型为SOC预测模型,通过引入遗传算法和蝗虫优化算法优化网络参数,建立高精度的锂电池SOC预测模型.从上述研究可以看出,采用群智能算法优化神经网络模型,避免梯度下降等传统优化算法造成局部最优问题已是当前研究的主要思路之一.此外,文献[60 ]通过建立基于核技术的径向基神经网络(radial basis function,RBF)解决锂电池SOC估计的非线性问题,并通过回溯搜索算法优化模型参数,将锂电池SOC估计误差降低在2%以内,而文献[61 ]提出广义回归神经网络(RBF神经网络的一种)实现了任一充放电状态下SOC的精确估计;文献[62 ]将模糊理论与神经网络相结合,通过设计模糊规则优化算法对网络结构进行优化,提高了电池SOC的预测精度.同时,研究者考虑锂电池SOC变化过程中的时序性,分别提出应用具有时间序列描绘特性的非线性自回归网络(nonlinear autoregressive with exogeneous inputs neural network,NARX)[63 ] 以及经典的深度学习网络(deep neural network,DNN),如长短期记忆循环神经网络(long short-term memory,LSTM)[64 ] 和门控循环神经网络(gated recurrent unit,GRU)[65 -66 ] 等模型,完成高性能的锂电池SOC估计,已取得良好的预测结果.在锂电池SOC估计的应用中,神经网络模型优势在于可以解决锂离子电池可测变量及特征与电池SOC之间复杂的非线性映射关系,模型的适应性好、精度高,但网络过大会导致模型参数大幅度增加,计算量过大,易陷入局部最优下的过/欠拟合,且对参数初始值较为敏感.表6 对比了用于锂电池SOC估计的不同神经网络优缺点. ...
... 3. 算法的计算复杂度高
NARX[63 ] 1.具有时间序列分析能力; ...
2
... 随着不同类型神经网络形式被提出,研究者将其分别应用于锂电池SOC估计中,以达到更高的估计精度.如文献[57 ]和[58]提出应用小型神经网络和极限学习机模型预测锂电池SOC,不同于传统极限学习机(extreme learning machine,ELM),通过引入核技术和狼群优化算法,增强了模型的非线性映射能力和预测精度;文献[56 ]和[59]以经典误差反向传播神经网络(backpropagation neural network,BPNN)模型为SOC预测模型,通过引入遗传算法和蝗虫优化算法优化网络参数,建立高精度的锂电池SOC预测模型.从上述研究可以看出,采用群智能算法优化神经网络模型,避免梯度下降等传统优化算法造成局部最优问题已是当前研究的主要思路之一.此外,文献[60 ]通过建立基于核技术的径向基神经网络(radial basis function,RBF)解决锂电池SOC估计的非线性问题,并通过回溯搜索算法优化模型参数,将锂电池SOC估计误差降低在2%以内,而文献[61 ]提出广义回归神经网络(RBF神经网络的一种)实现了任一充放电状态下SOC的精确估计;文献[62 ]将模糊理论与神经网络相结合,通过设计模糊规则优化算法对网络结构进行优化,提高了电池SOC的预测精度.同时,研究者考虑锂电池SOC变化过程中的时序性,分别提出应用具有时间序列描绘特性的非线性自回归网络(nonlinear autoregressive with exogeneous inputs neural network,NARX)[63 ] 以及经典的深度学习网络(deep neural network,DNN),如长短期记忆循环神经网络(long short-term memory,LSTM)[64 ] 和门控循环神经网络(gated recurrent unit,GRU)[65 -66 ] 等模型,完成高性能的锂电池SOC估计,已取得良好的预测结果.在锂电池SOC估计的应用中,神经网络模型优势在于可以解决锂离子电池可测变量及特征与电池SOC之间复杂的非线性映射关系,模型的适应性好、精度高,但网络过大会导致模型参数大幅度增加,计算量过大,易陷入局部最优下的过/欠拟合,且对参数初始值较为敏感.表6 对比了用于锂电池SOC估计的不同神经网络优缺点. ...
... 2.模型性能受数据影响很大
LSTM[64 ] 1.强大时间序列分析能力可以反映SOC时序特点; ...
2
... 随着不同类型神经网络形式被提出,研究者将其分别应用于锂电池SOC估计中,以达到更高的估计精度.如文献[57 ]和[58]提出应用小型神经网络和极限学习机模型预测锂电池SOC,不同于传统极限学习机(extreme learning machine,ELM),通过引入核技术和狼群优化算法,增强了模型的非线性映射能力和预测精度;文献[56 ]和[59]以经典误差反向传播神经网络(backpropagation neural network,BPNN)模型为SOC预测模型,通过引入遗传算法和蝗虫优化算法优化网络参数,建立高精度的锂电池SOC预测模型.从上述研究可以看出,采用群智能算法优化神经网络模型,避免梯度下降等传统优化算法造成局部最优问题已是当前研究的主要思路之一.此外,文献[60 ]通过建立基于核技术的径向基神经网络(radial basis function,RBF)解决锂电池SOC估计的非线性问题,并通过回溯搜索算法优化模型参数,将锂电池SOC估计误差降低在2%以内,而文献[61 ]提出广义回归神经网络(RBF神经网络的一种)实现了任一充放电状态下SOC的精确估计;文献[62 ]将模糊理论与神经网络相结合,通过设计模糊规则优化算法对网络结构进行优化,提高了电池SOC的预测精度.同时,研究者考虑锂电池SOC变化过程中的时序性,分别提出应用具有时间序列描绘特性的非线性自回归网络(nonlinear autoregressive with exogeneous inputs neural network,NARX)[63 ] 以及经典的深度学习网络(deep neural network,DNN),如长短期记忆循环神经网络(long short-term memory,LSTM)[64 ] 和门控循环神经网络(gated recurrent unit,GRU)[65 -66 ] 等模型,完成高性能的锂电池SOC估计,已取得良好的预测结果.在锂电池SOC估计的应用中,神经网络模型优势在于可以解决锂离子电池可测变量及特征与电池SOC之间复杂的非线性映射关系,模型的适应性好、精度高,但网络过大会导致模型参数大幅度增加,计算量过大,易陷入局部最优下的过/欠拟合,且对参数初始值较为敏感.表6 对比了用于锂电池SOC估计的不同神经网络优缺点. ...
... 2.模型性能受数据影响很大
LSTM[64 ] 1.强大时间序列分析能力可以反映SOC时序特点; ...
2
... 随着不同类型神经网络形式被提出,研究者将其分别应用于锂电池SOC估计中,以达到更高的估计精度.如文献[57 ]和[58]提出应用小型神经网络和极限学习机模型预测锂电池SOC,不同于传统极限学习机(extreme learning machine,ELM),通过引入核技术和狼群优化算法,增强了模型的非线性映射能力和预测精度;文献[56 ]和[59]以经典误差反向传播神经网络(backpropagation neural network,BPNN)模型为SOC预测模型,通过引入遗传算法和蝗虫优化算法优化网络参数,建立高精度的锂电池SOC预测模型.从上述研究可以看出,采用群智能算法优化神经网络模型,避免梯度下降等传统优化算法造成局部最优问题已是当前研究的主要思路之一.此外,文献[60 ]通过建立基于核技术的径向基神经网络(radial basis function,RBF)解决锂电池SOC估计的非线性问题,并通过回溯搜索算法优化模型参数,将锂电池SOC估计误差降低在2%以内,而文献[61 ]提出广义回归神经网络(RBF神经网络的一种)实现了任一充放电状态下SOC的精确估计;文献[62 ]将模糊理论与神经网络相结合,通过设计模糊规则优化算法对网络结构进行优化,提高了电池SOC的预测精度.同时,研究者考虑锂电池SOC变化过程中的时序性,分别提出应用具有时间序列描绘特性的非线性自回归网络(nonlinear autoregressive with exogeneous inputs neural network,NARX)[63 ] 以及经典的深度学习网络(deep neural network,DNN),如长短期记忆循环神经网络(long short-term memory,LSTM)[64 ] 和门控循环神经网络(gated recurrent unit,GRU)[65 -66 ] 等模型,完成高性能的锂电池SOC估计,已取得良好的预测结果.在锂电池SOC估计的应用中,神经网络模型优势在于可以解决锂离子电池可测变量及特征与电池SOC之间复杂的非线性映射关系,模型的适应性好、精度高,但网络过大会导致模型参数大幅度增加,计算量过大,易陷入局部最优下的过/欠拟合,且对参数初始值较为敏感.表6 对比了用于锂电池SOC估计的不同神经网络优缺点. ...
... 4.参数多易过度拟合
GRU [65 ] 1.相比而言参数较少,降低了过拟合风险; ...
2
... 随着不同类型神经网络形式被提出,研究者将其分别应用于锂电池SOC估计中,以达到更高的估计精度.如文献[57 ]和[58]提出应用小型神经网络和极限学习机模型预测锂电池SOC,不同于传统极限学习机(extreme learning machine,ELM),通过引入核技术和狼群优化算法,增强了模型的非线性映射能力和预测精度;文献[56 ]和[59]以经典误差反向传播神经网络(backpropagation neural network,BPNN)模型为SOC预测模型,通过引入遗传算法和蝗虫优化算法优化网络参数,建立高精度的锂电池SOC预测模型.从上述研究可以看出,采用群智能算法优化神经网络模型,避免梯度下降等传统优化算法造成局部最优问题已是当前研究的主要思路之一.此外,文献[60 ]通过建立基于核技术的径向基神经网络(radial basis function,RBF)解决锂电池SOC估计的非线性问题,并通过回溯搜索算法优化模型参数,将锂电池SOC估计误差降低在2%以内,而文献[61 ]提出广义回归神经网络(RBF神经网络的一种)实现了任一充放电状态下SOC的精确估计;文献[62 ]将模糊理论与神经网络相结合,通过设计模糊规则优化算法对网络结构进行优化,提高了电池SOC的预测精度.同时,研究者考虑锂电池SOC变化过程中的时序性,分别提出应用具有时间序列描绘特性的非线性自回归网络(nonlinear autoregressive with exogeneous inputs neural network,NARX)[63 ] 以及经典的深度学习网络(deep neural network,DNN),如长短期记忆循环神经网络(long short-term memory,LSTM)[64 ] 和门控循环神经网络(gated recurrent unit,GRU)[65 -66 ] 等模型,完成高性能的锂电池SOC估计,已取得良好的预测结果.在锂电池SOC估计的应用中,神经网络模型优势在于可以解决锂离子电池可测变量及特征与电池SOC之间复杂的非线性映射关系,模型的适应性好、精度高,但网络过大会导致模型参数大幅度增加,计算量过大,易陷入局部最优下的过/欠拟合,且对参数初始值较为敏感.表6 对比了用于锂电池SOC估计的不同神经网络优缺点. ...
... 4.参数多易过度拟合
GRU [65 ] 1.相比而言参数较少,降低了过拟合风险; ...
1
... 随着不同类型神经网络形式被提出,研究者将其分别应用于锂电池SOC估计中,以达到更高的估计精度.如文献[57 ]和[58]提出应用小型神经网络和极限学习机模型预测锂电池SOC,不同于传统极限学习机(extreme learning machine,ELM),通过引入核技术和狼群优化算法,增强了模型的非线性映射能力和预测精度;文献[56 ]和[59]以经典误差反向传播神经网络(backpropagation neural network,BPNN)模型为SOC预测模型,通过引入遗传算法和蝗虫优化算法优化网络参数,建立高精度的锂电池SOC预测模型.从上述研究可以看出,采用群智能算法优化神经网络模型,避免梯度下降等传统优化算法造成局部最优问题已是当前研究的主要思路之一.此外,文献[60 ]通过建立基于核技术的径向基神经网络(radial basis function,RBF)解决锂电池SOC估计的非线性问题,并通过回溯搜索算法优化模型参数,将锂电池SOC估计误差降低在2%以内,而文献[61 ]提出广义回归神经网络(RBF神经网络的一种)实现了任一充放电状态下SOC的精确估计;文献[62 ]将模糊理论与神经网络相结合,通过设计模糊规则优化算法对网络结构进行优化,提高了电池SOC的预测精度.同时,研究者考虑锂电池SOC变化过程中的时序性,分别提出应用具有时间序列描绘特性的非线性自回归网络(nonlinear autoregressive with exogeneous inputs neural network,NARX)[63 ] 以及经典的深度学习网络(deep neural network,DNN),如长短期记忆循环神经网络(long short-term memory,LSTM)[64 ] 和门控循环神经网络(gated recurrent unit,GRU)[65 -66 ] 等模型,完成高性能的锂电池SOC估计,已取得良好的预测结果.在锂电池SOC估计的应用中,神经网络模型优势在于可以解决锂离子电池可测变量及特征与电池SOC之间复杂的非线性映射关系,模型的适应性好、精度高,但网络过大会导致模型参数大幅度增加,计算量过大,易陷入局部最优下的过/欠拟合,且对参数初始值较为敏感.表6 对比了用于锂电池SOC估计的不同神经网络优缺点. ...
1
... 随着不同类型神经网络形式被提出,研究者将其分别应用于锂电池SOC估计中,以达到更高的估计精度.如文献[57 ]和[58]提出应用小型神经网络和极限学习机模型预测锂电池SOC,不同于传统极限学习机(extreme learning machine,ELM),通过引入核技术和狼群优化算法,增强了模型的非线性映射能力和预测精度;文献[56 ]和[59]以经典误差反向传播神经网络(backpropagation neural network,BPNN)模型为SOC预测模型,通过引入遗传算法和蝗虫优化算法优化网络参数,建立高精度的锂电池SOC预测模型.从上述研究可以看出,采用群智能算法优化神经网络模型,避免梯度下降等传统优化算法造成局部最优问题已是当前研究的主要思路之一.此外,文献[60 ]通过建立基于核技术的径向基神经网络(radial basis function,RBF)解决锂电池SOC估计的非线性问题,并通过回溯搜索算法优化模型参数,将锂电池SOC估计误差降低在2%以内,而文献[61 ]提出广义回归神经网络(RBF神经网络的一种)实现了任一充放电状态下SOC的精确估计;文献[62 ]将模糊理论与神经网络相结合,通过设计模糊规则优化算法对网络结构进行优化,提高了电池SOC的预测精度.同时,研究者考虑锂电池SOC变化过程中的时序性,分别提出应用具有时间序列描绘特性的非线性自回归网络(nonlinear autoregressive with exogeneous inputs neural network,NARX)[63 ] 以及经典的深度学习网络(deep neural network,DNN),如长短期记忆循环神经网络(long short-term memory,LSTM)[64 ] 和门控循环神经网络(gated recurrent unit,GRU)[65 -66 ] 等模型,完成高性能的锂电池SOC估计,已取得良好的预测结果.在锂电池SOC估计的应用中,神经网络模型优势在于可以解决锂离子电池可测变量及特征与电池SOC之间复杂的非线性映射关系,模型的适应性好、精度高,但网络过大会导致模型参数大幅度增加,计算量过大,易陷入局部最优下的过/欠拟合,且对参数初始值较为敏感.表6 对比了用于锂电池SOC估计的不同神经网络优缺点. ...
2
... 为了不断提高支持向量机估计电池SOC的泛用能力,研究人员通过改进支持向量机模型,提升其在锂电池SOC估计中的应用水平.如文献[67 ]通过分析群智能优化算法对支持向量机参数优化结果,提高SOC估计精度;而文献[68 ]利用最小二乘法支持向量机收敛速度快、全局搜索强的优势,提高电池SOC预测能力;文献[69 ]提出基于瑞利熵理论改进传统最小二乘支持向量机算法的稀疏性,同时利用粒子群优化算法搜索改进最小二乘支持向量机算法中的最优超参数组合,锂电池容量估计误差小于1.5%.相比于神经网络模型,基于支持向量机的锂电池SOC估计模型参数少导致计算量小,对样本数据量要求不高,非常适用于电池这类测试过程困难的小样本场景,且估计精度较高.但是支持向量回归模型是核函数选择没有通用标准,需要不断尝试,在大数据样本场景中,核函数映射维度过高,导致计算量过大,将变得不太适合使用. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
2
... 为了不断提高支持向量机估计电池SOC的泛用能力,研究人员通过改进支持向量机模型,提升其在锂电池SOC估计中的应用水平.如文献[67 ]通过分析群智能优化算法对支持向量机参数优化结果,提高SOC估计精度;而文献[68 ]利用最小二乘法支持向量机收敛速度快、全局搜索强的优势,提高电池SOC预测能力;文献[69 ]提出基于瑞利熵理论改进传统最小二乘支持向量机算法的稀疏性,同时利用粒子群优化算法搜索改进最小二乘支持向量机算法中的最优超参数组合,锂电池容量估计误差小于1.5%.相比于神经网络模型,基于支持向量机的锂电池SOC估计模型参数少导致计算量小,对样本数据量要求不高,非常适用于电池这类测试过程困难的小样本场景,且估计精度较高.但是支持向量回归模型是核函数选择没有通用标准,需要不断尝试,在大数据样本场景中,核函数映射维度过高,导致计算量过大,将变得不太适合使用. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
1
... 为了不断提高支持向量机估计电池SOC的泛用能力,研究人员通过改进支持向量机模型,提升其在锂电池SOC估计中的应用水平.如文献[67 ]通过分析群智能优化算法对支持向量机参数优化结果,提高SOC估计精度;而文献[68 ]利用最小二乘法支持向量机收敛速度快、全局搜索强的优势,提高电池SOC预测能力;文献[69 ]提出基于瑞利熵理论改进传统最小二乘支持向量机算法的稀疏性,同时利用粒子群优化算法搜索改进最小二乘支持向量机算法中的最优超参数组合,锂电池容量估计误差小于1.5%.相比于神经网络模型,基于支持向量机的锂电池SOC估计模型参数少导致计算量小,对样本数据量要求不高,非常适用于电池这类测试过程困难的小样本场景,且估计精度较高.但是支持向量回归模型是核函数选择没有通用标准,需要不断尝试,在大数据样本场景中,核函数映射维度过高,导致计算量过大,将变得不太适合使用. ...
1
... 为了不断提高支持向量机估计电池SOC的泛用能力,研究人员通过改进支持向量机模型,提升其在锂电池SOC估计中的应用水平.如文献[67 ]通过分析群智能优化算法对支持向量机参数优化结果,提高SOC估计精度;而文献[68 ]利用最小二乘法支持向量机收敛速度快、全局搜索强的优势,提高电池SOC预测能力;文献[69 ]提出基于瑞利熵理论改进传统最小二乘支持向量机算法的稀疏性,同时利用粒子群优化算法搜索改进最小二乘支持向量机算法中的最优超参数组合,锂电池容量估计误差小于1.5%.相比于神经网络模型,基于支持向量机的锂电池SOC估计模型参数少导致计算量小,对样本数据量要求不高,非常适用于电池这类测试过程困难的小样本场景,且估计精度较高.但是支持向量回归模型是核函数选择没有通用标准,需要不断尝试,在大数据样本场景中,核函数映射维度过高,导致计算量过大,将变得不太适合使用. ...
2
... 为了不断提高支持向量机估计电池SOC的泛用能力,研究人员通过改进支持向量机模型,提升其在锂电池SOC估计中的应用水平.如文献[67 ]通过分析群智能优化算法对支持向量机参数优化结果,提高SOC估计精度;而文献[68 ]利用最小二乘法支持向量机收敛速度快、全局搜索强的优势,提高电池SOC预测能力;文献[69 ]提出基于瑞利熵理论改进传统最小二乘支持向量机算法的稀疏性,同时利用粒子群优化算法搜索改进最小二乘支持向量机算法中的最优超参数组合,锂电池容量估计误差小于1.5%.相比于神经网络模型,基于支持向量机的锂电池SOC估计模型参数少导致计算量小,对样本数据量要求不高,非常适用于电池这类测试过程困难的小样本场景,且估计精度较高.但是支持向量回归模型是核函数选择没有通用标准,需要不断尝试,在大数据样本场景中,核函数映射维度过高,导致计算量过大,将变得不太适合使用. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
2
... 为了不断提高支持向量机估计电池SOC的泛用能力,研究人员通过改进支持向量机模型,提升其在锂电池SOC估计中的应用水平.如文献[67 ]通过分析群智能优化算法对支持向量机参数优化结果,提高SOC估计精度;而文献[68 ]利用最小二乘法支持向量机收敛速度快、全局搜索强的优势,提高电池SOC预测能力;文献[69 ]提出基于瑞利熵理论改进传统最小二乘支持向量机算法的稀疏性,同时利用粒子群优化算法搜索改进最小二乘支持向量机算法中的最优超参数组合,锂电池容量估计误差小于1.5%.相比于神经网络模型,基于支持向量机的锂电池SOC估计模型参数少导致计算量小,对样本数据量要求不高,非常适用于电池这类测试过程困难的小样本场景,且估计精度较高.但是支持向量回归模型是核函数选择没有通用标准,需要不断尝试,在大数据样本场景中,核函数映射维度过高,导致计算量过大,将变得不太适合使用. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
2
... 除了上述多种神经网络以及支持向量机外,高斯过程回归(Gaussian process regression,GPR)作为一种常用模型被用于锂电池SOC估计中,如文献[70 ]以在线实时采集的电池电压、电流和温度为输入,通过高斯回归模型估计电池SOC概率分布,形成估计值不确定性的量化分析;而文献[71 ]和[72]通过多个高斯分布加权平均的混合方式和引入前一时刻电池SOC的方式降低测量误差和模型误差影响,提升SOC估计精度.不同于神经网络和支持向量机模型,高斯过程回归模型是一种随机过程下的概率估计模型,高斯概率分布先验假设条件以及核函数形式等因素制约其在SOC估计中的深度应用,但是该方法模型简单易实现,非常适合电池SOC的在线快速检测,已经成为一种重要的电池SOC估计方法. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8 方法类型 估计方法 方法精度 方法复杂度 方法数据量 方法计算量 实时检测性 基于实验测试计算的估计方法 开路电压法[22 ] ** * * * * 放电法[21 ] ** *** * * * 安时积分法[4 ] *** *** * ** *** 电导法[23 ] *** ** ** ** * 交流阻抗法[24 ] **** **** *** ** * 基于模型驱动的估计方法 卡尔曼及其改进滤波[35 -36 ] *** *** *** *** **** 粒子滤波[50 -52 ] **** *** *** *** **** H无穷滤波[53 ] *** **** *** *** **** 基于递推最小二乘滤波[54 ] *** *** *** *** **** 基于数据驱动的估计方法 神经网络类[61 ,62 ] **** **** ***** **** **** 支持向量类[67 -69 ] *** *** **** *** **** 高斯过程回归[70 ] *** ** **** *** **** 基于数模驱动的估计方法 卡尔曼+ ...
2
... 除了上述多种神经网络以及支持向量机外,高斯过程回归(Gaussian process regression,GPR)作为一种常用模型被用于锂电池SOC估计中,如文献[70 ]以在线实时采集的电池电压、电流和温度为输入,通过高斯回归模型估计电池SOC概率分布,形成估计值不确定性的量化分析;而文献[71 ]和[72]通过多个高斯分布加权平均的混合方式和引入前一时刻电池SOC的方式降低测量误差和模型误差影响,提升SOC估计精度.不同于神经网络和支持向量机模型,高斯过程回归模型是一种随机过程下的概率估计模型,高斯概率分布先验假设条件以及核函数形式等因素制约其在SOC估计中的深度应用,但是该方法模型简单易实现,非常适合电池SOC的在线快速检测,已经成为一种重要的电池SOC估计方法. ...
... Performance comparison of lithium battery SOC estimation technology
Table 8