目前我国真正达到低碳节能标准意义的建筑不到10%,其他的90%都是耗能建筑,而且新建房屋建筑中95%以上仍为高能耗建筑,但我国资源占有量不到世界平均水平的20%,单位建筑面积能耗却是气候相近发达国家的3~5倍。因此针对超低能耗、近零能耗建筑,开发安全、高效、绿色、经济、耐久的保温装饰一体化板保温系统具有极其重要的价值,而储能电池是智能传感应用的关键。现今,锂离子电池(lithium-ion batteries,LIBs)已成为储能系统电源的主要选择[1]。为提高电池系统实际运行的安全性、稳定性和可靠性[2],电池SOH估计成为至关重要的研究热点[3-4]。SOH通常根据容量衰减和内阻变化来对电池老化程度进行定量评估[5]。然而,目前无论是容量还是内阻都不能用市售的传感器直接测量[6]。因此,间接分析方法是开发SOH估计方法的一个重要方向。间接分析的关键在于如何能从低成本传感器采集的数据中提取出间接健康特征参数来表征SOH。
曲线相似性分析是一种常用的聚类分析方法,在大规模电池组故障分析研究中,通过对不同电池单体的电压曲线聚类,能够分析出电池组的健康状况[10]。对同一电池单体不同充放循环的电压曲线进行相似性分析可以估计出电池单体SOH。参考文献[11]引入平均弗雷歇距离(average Fréchet distance,AFD)方法来确定充放电曲线的相似性,实验表明AFD是良好的SOH估计参数。参考文献[12]为解决不同长度的循环曲线序列,使用动态时间规整(dynamic time warping,DTW)算法和长短期记忆网络(long short term memory networks,LSTM)的组合模型估计电池的SOH。
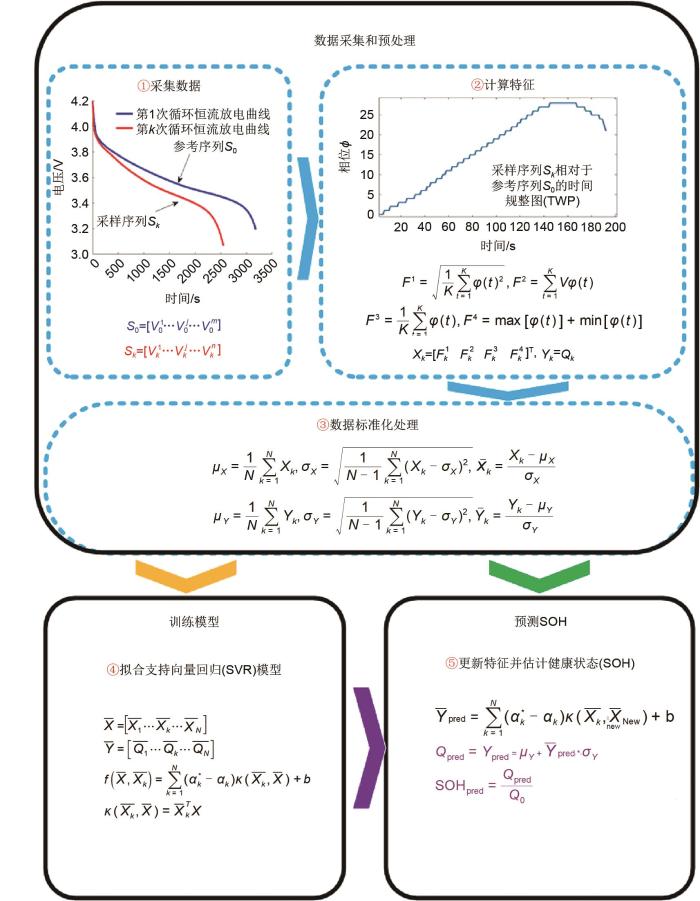
基于曲线相似性分析思想,本研究提出了一种使用时间规整图TWP提取间接健康特征参数,使用支持SVR模型估计SOH的方法。流程如图1所示。
图 1
首先,通过等间隔采样获取LIBs初始循环的放电电压曲线作为参考序列,依次获取不同循环的放电电压曲线作为采样序列。然后,使用DTW算法找出最优规划路径,通过坐标转换获得TWP并提取出4个间接健康特征。其次,对健康特征数据和容量数据进行标准化处理,获得标准化的训练数据集。接着,用处理后的数据集训练基于线性核的SVR模型。最后,通过对新循环的电压曲线进行采样获得间接健康特征,使用训练好的SVR模型估计SOH。
1 方法
1.1 特征提取算法
1.1.1 动态时间规整
动态时间规整是一种准确率高、鲁棒性强的时间序列相似性度量方法,能够通过弯曲时间序列的时域对时间序列的数据点进行匹配,不仅能够得到更好的形态度量效果,而且能够度量两条非等长的时间序列相似性[13]。
考虑两条不同长度的时间序列
其中
其中,
①边界线:
②单调性:对于给定的
③连续性:对于给定的
可以使用动态规划方法求解
其中初始条件D(1,1)=d11。
图 2
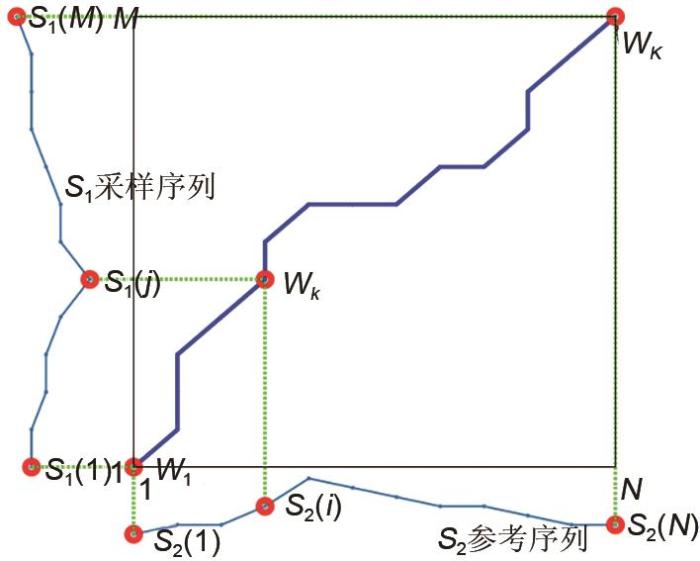
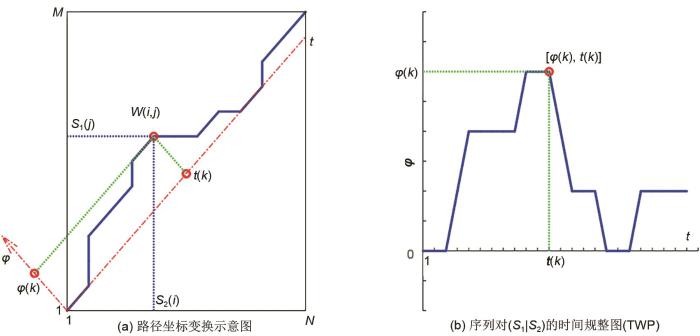
1.1.2 时间规整图
其中
图 3
1.1.3 间接健康特征
TWP将DTW中的二维的最佳规整路径W压缩成一维的相位差异序列
其中,
在LIBs循环老化实验中,考虑电池充放循环中放电时间较长,且曲线长度不一致。为了缩小模型规模和统一参数数目。选择初始循环的放电电压曲线作为参考序列S0,选择其余循环的放电电压曲线作为采样序列Si,依次使用上述算法获得采样序列与参考序列的相位差异序列
1.2 SOH拟合模型
对于数据集{(X1,Y1),(X2,Y2)…(XN,YN )},考虑线性关系的时候,有回归函数:
其中W和b是模型的权重参数和偏置参数。支持向量机回归SVR将拟合
其中,C为惩罚参数,用于控制对位于ε边界之外的观测值施加的惩罚,这有助于防止过度拟合。松弛变量ξ和
其中
引入核函数之后可得回归函数:
核函数有多种选择,包括线性核、多项式核、高斯核以及混合核。
1.3 评价指标
为了评估选取的4个间接健康指标能否反映电池容量衰减特性。选择三个相关性指标进行评价:皮尔森(Pearson)系数、斯皮尔曼(Spearman)系数、肯德尔(Kendall)系数。
其中,
为了更全面地评估所提方法的准确性,给出三个常用的评价指标:RMSE、MAE、MAPE。
其中,
为了评估所提方法应用于不同电池的稳定性,使用不同电池实验的同类型准确性指标的样本标准差和四分位差两个指标说明方法的稳定性。
其中,
2 实验验证与分析
2.1 数据描述与实验过程
为了验证所提出方法估计SOH的准确性及其适用性,本工作使用了2个开源数据和实际储能电站运行数据进行实验,数据集的相关信息见表1。本工作所有的实验在CPU型号为i7-6500U@2.50 GHz,RAM内存为12 G的设备上使用Matlab R2021a软件进行分析。所提算法由特征提取和拟合模型两部分组成。实验使用NASA数据集,首先,根据相关系数验证TWP算法提取出的4个间接健康特征能否反映电池容量衰减特性。然后,评估TWP类型的特征提取算法分别接入SVR模型和GPR模型后的准确性。使用UL-PUR数据集验证TWP-SVR和TWP-GPR两种方法的准确性和稳定性,最后使用储能电站的数据验证所提TWP-SVR方法的准确性和稳定性。
表1 实验数据集信息
Table 1
2.2 特征提取算法的验证
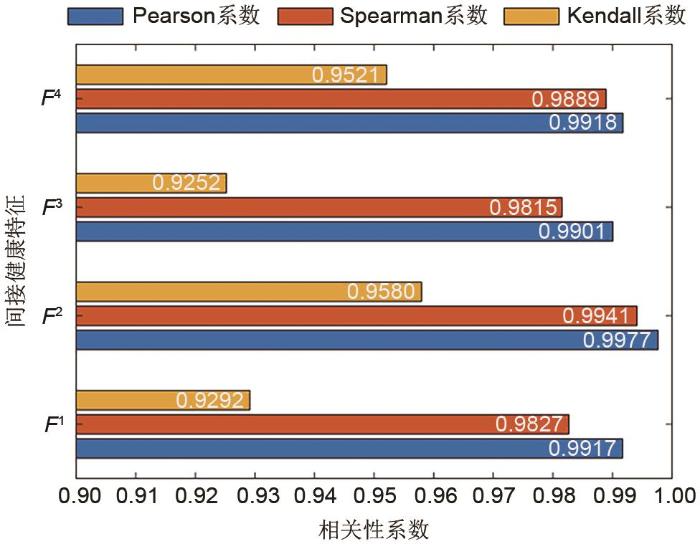
为了验证TWP提取4个间接健康特征与电池容量衰减的相关性,本工作使用NASA数据集中5、6、7、18号电池进行分析。在每一次充放循环实验中,选取2 A(1 C)恒定电流(CC)放电阶段的电压曲线作为实验数据。注意到电压数据是非等间隔采样获得,所以在提取特征之前先进行等间隔插值处理。将第1次循环的放电电压曲线作为参考序列,不同循环的放电电压曲线作为采样序列,利用
图 4
图 4
间接健康特征和衰减容量的相关性
Fig. 4
Correlation between indirect health characteristics and attenuation capacity
表 2 间接健康特征和衰减容量的相关系数
Table 2
| 电池 | 相关系数 | 间接健康特征 | |||
|---|---|---|---|---|---|
| F1 | F2 | F3 | F4 | ||
| 5 | Pearson | 0.9949 | 0.9978 | 0.9926 | 0.9949 |
| Spearman | 0.9725 | 0.9926 | 0.9701 | 0.9826 | |
| Kendall | 0.9013 | 0.9520 | 0.8959 | 0.9359 | |
| 6 | Pearson | 0.9933 | 0.9988 | 0.9948 | 0.9942 |
| Spearman | 0.9989 | 0.9990 | 0.9985 | 0.9993 | |
| Kendall | 0.9805 | 0.9825 | 0.9773 | 0.9859 | |
| 7 | Pearson | 0.9891 | 0.9969 | 0.9874 | 0.9872 |
| Spearman | 0.9642 | 0.9897 | 0.9637 | 0.9767 | |
| Kendall | 0.8811 | 0.9397 | 0.8786 | 0.9179 | |
| 18 | Pearson | 0.9895 | 0.9972 | 9.8550 | 0.9908 |
| Spearman | 0.9951 | 0.9952 | 0.9938 | 0.9971 | |
| Kendall | 0.9537 | 0.9576 | 0.9490 | 0.9686 | |
为了验证本工作所提特征提取算法的准确性,本工作使用上文提到的NASA开源的4个2000 mAh的电池数据与2种算法进行比较分析。这些算法是由特征提取和拟合模型组合的方法,算法详细说明见表3。
表 3 实验所用算法信息
Table 3
| 算法 | 输入数据 | 特征提取算法 | 输出特征 | 拟合模型参数 |
|---|---|---|---|---|
| TWP-SVR | 充放电压曲线 | TWP | F1, F2, F3, F4 | 1. 核函数:线性核 |
| 2. 惩罚参数:1 | ||||
| 3. 不敏感参数:输出变量的四分位数范围对标准差的十分之一的估计值 | ||||
| TWP-GPR | 充放电压曲线 | TWP | F1, F2, F3, F4 | 1. 协方差函数:平方指数核 |
| 2. 噪声标准偏差的初始值:输出变量的标准差除以根号二 |
图 5
图 5
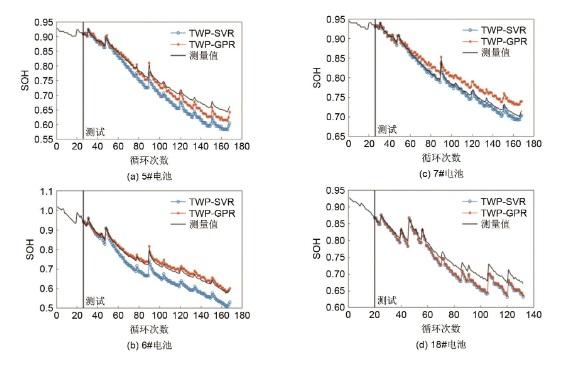
基于TWP特征提取算法的4个电池SOH估计值
Fig. 5
SOH estimation of four batteries based on TWP feature extraction algorithm
图 6
图 6
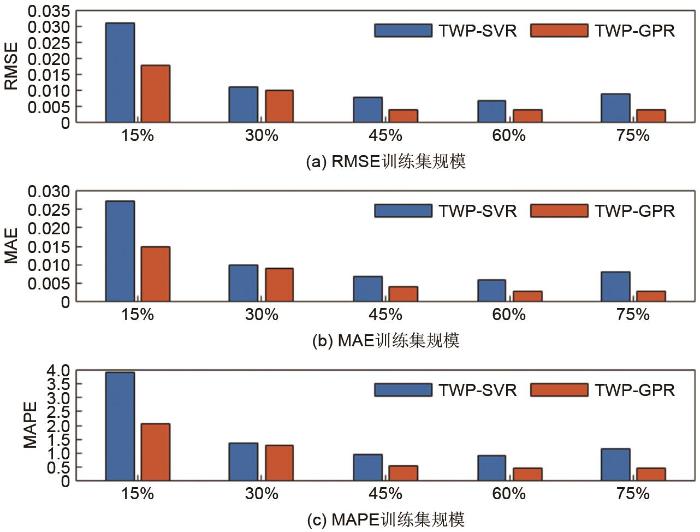
基于TWP特征提取算法的准确性评价指标
Fig. 6
Accuracy evaluation index based on TWP feature extraction algorithm
2.3 拟合模型的选择
实验使用TWP算法获取间接健康特征,拟合模型选择SVR和GPR作为比较。考虑放电阶段不同的截止电压,使用(UL-PUR)开源的镍钴铝酸锂(NCA) 电池容量衰减数据集。此数据集提供了10个以1.7 A(0.5 C)恒流放电至2.7 V的NCA电池和11个以1.7 A(0.5 C)恒流放电至2.9 V的NCA电池。本工作使用每个电池前15%循环中恒流放电阶段的电压曲线作为训练数据。
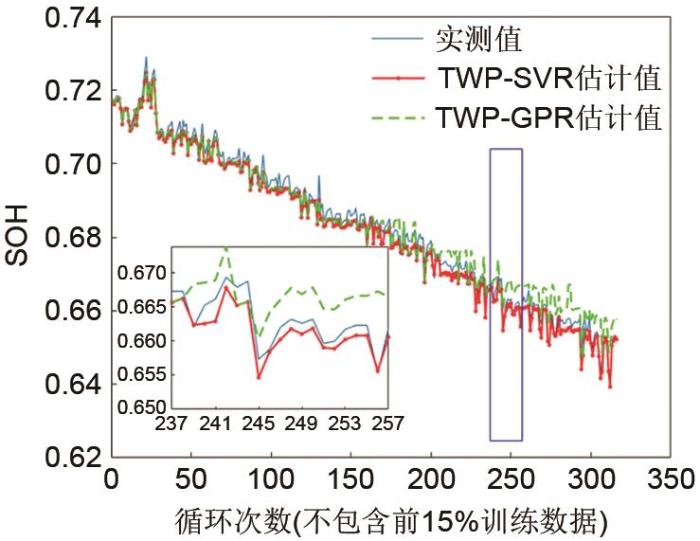
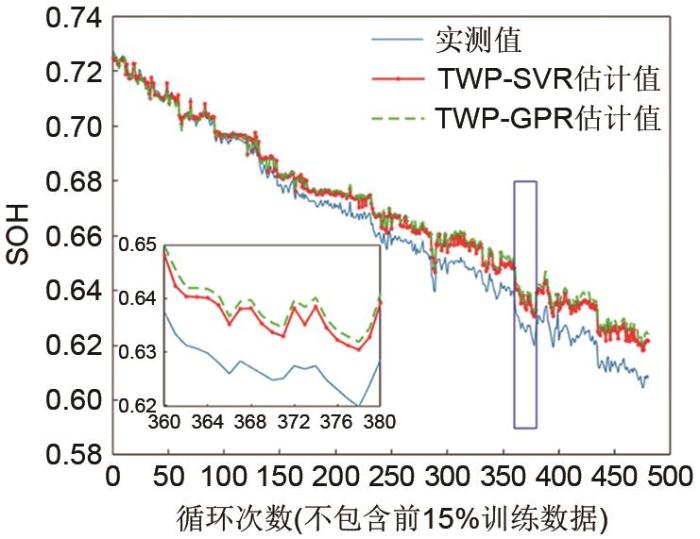
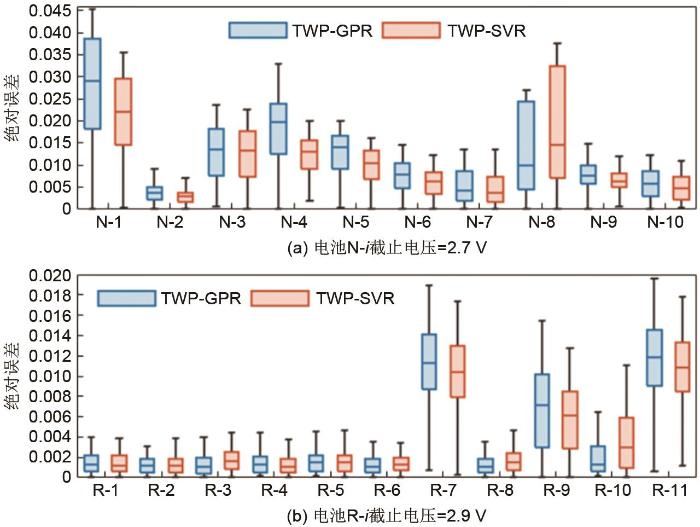
使用两种模型对截止电压分别为2.7 V和2.9 V的电池进行实验。图7和图8展示了两种模型在截止电压为2.9 V的N-2和N-7号电池的SOH估计情况,图9和图10展示了两种模型在截止电压为2.7 V的R-2和R-9号电池的SOH估计情况,两种模型的SOH估计值的绝对误差分布如图11所示。由图11(a)可以看出,当截止电压为2.7 V时,对于不同的电池,两种模型的SOH估计值的绝对误差分布差异较大;对于同一电池,两种模型的SOH估计值的绝对误差分布较为接近。由图11(b)可以看出,当截止电压为2.9 V时,对于大部分的电池,两种模型的SOH估计值的绝对误差分布差异较小,少部分电池的SOH估计值的绝对误差分布差异较大;对于同一电池,两种模型的SOH估计值的绝对误差分布较为接近。
图 7
图 7
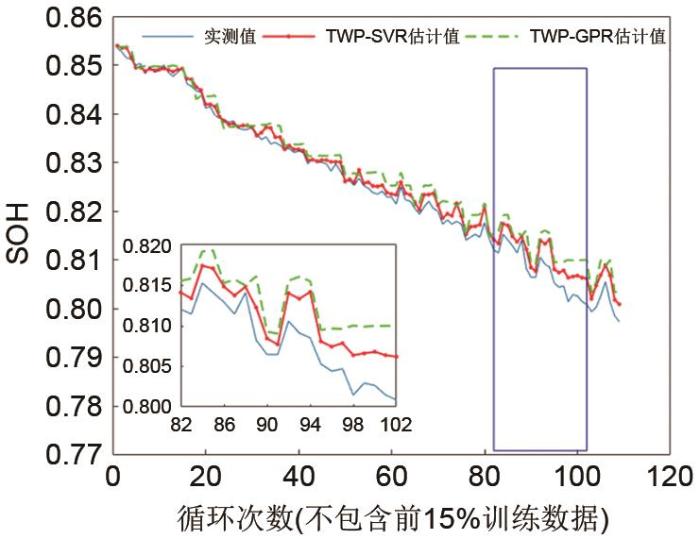
基于截止电压为2.9 V的N-2号电池的两种模型的SOH估计比较
Fig. 7
Comparison of SOH estimation based on two models of N-2 battery with cut-off voltage of 2.9 V
图 8
图 8
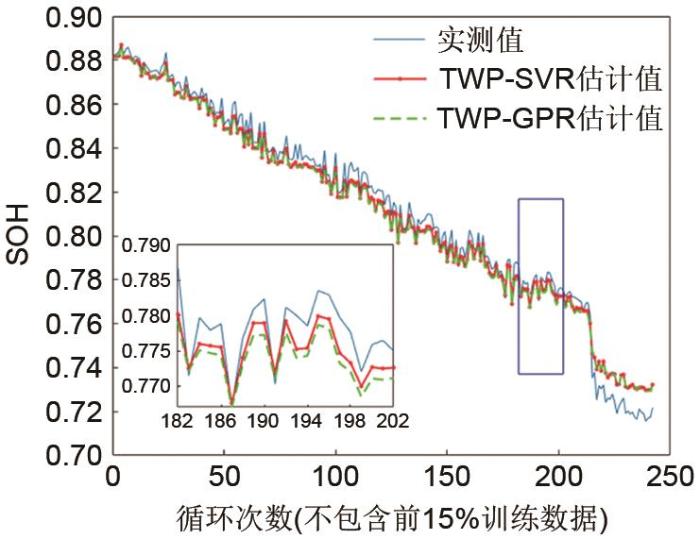
基于截止电压为2.9 V的N-7号电池的两种模型的SOH估计比较
Fig. 8
Comparison of SOH estimation based on two models of N-7 battery with cut-off voltage of 2.9 V
图 9
图 9
基于截止电压为2.7 V的R-2号电池的两种模型的SOH估计比较
Fig. 9
Comparison of SOH estimation of two models based on R-2 battery with cut-off voltage of 2.7 V
图 10
图 10
基于截止电压为2.7 V的R-9号电池的两种模型的SOH估计比较
Fig. 10
Comparison of SOH estimation of two models based on R-9 battery with cut-off voltage of 2.7 V
图 11
图 11
基于不同截至电压的两种模型SOH估计值的绝对误差分布
Fig. 11
Absolute error distribution of SOH estimation of two models based on different cut-off voltages
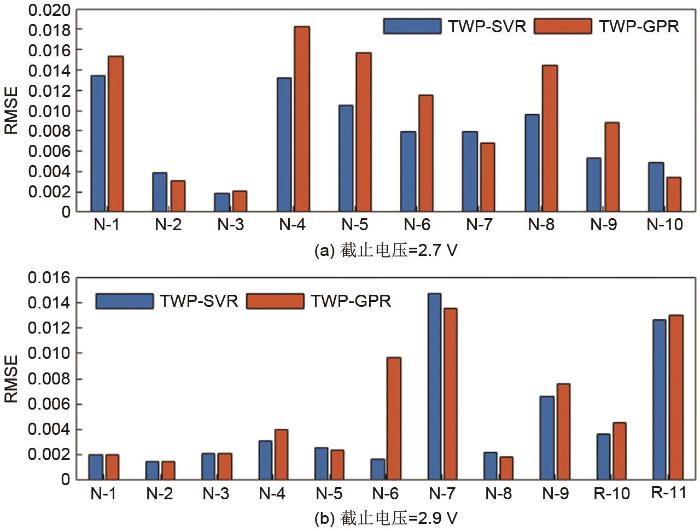
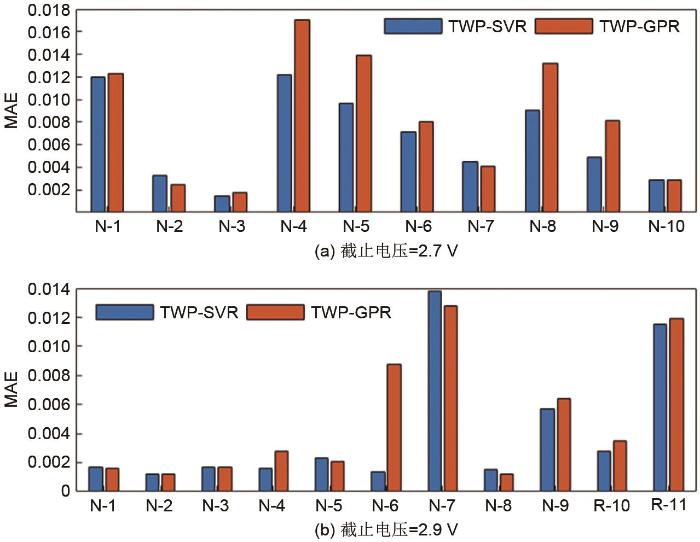
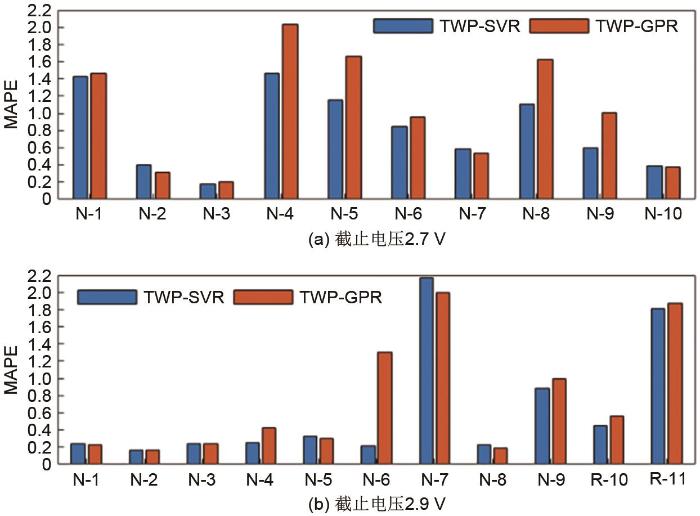
两种模型的SOH估计值的3种评价指标如图12、13、14所示。由图12(a)、13(a)、14(a)可以看出,当截止电压为2.7 V时,对于不同的电池,两种模型的SOH估计值的RMSE、MAE、MAPE指标波动较大;对于同一电池,TWP-SVR模型的RMSE、MAE和MAPE指标要小于TWP-GPR的RMSE指标。由图12(b)、13(b)、14(b)可以看出,当截止电压为2.9 V时,对于大部分的电池,TWP-SVR模型的SOH估计值的RMSE、MAE和MAPE指标小于TWP-GPR模型,个别电池例外。对于不同电池,TWP-SVR模型的SOH估计值的RMSE、MAE和MAPE指标较为平稳,少数电池例外;TWP-GPR模型的SOH估计值的RMSE、MAE和MAPE指标波动较大。
图 12
图 12
基于不同截止电压的两种模型的RMSE
Fig. 12
RMSE of two models based on different cut-off voltages
图 13
图 13
基于不同截止电压的两种模型的MAE
Fig. 13
MAE of two models based on different cut-off voltages
图 14
图 14
基于不同截止电压的两种模型的MAPE
Fig. 14
MAPE of two models based on different cut-off voltages
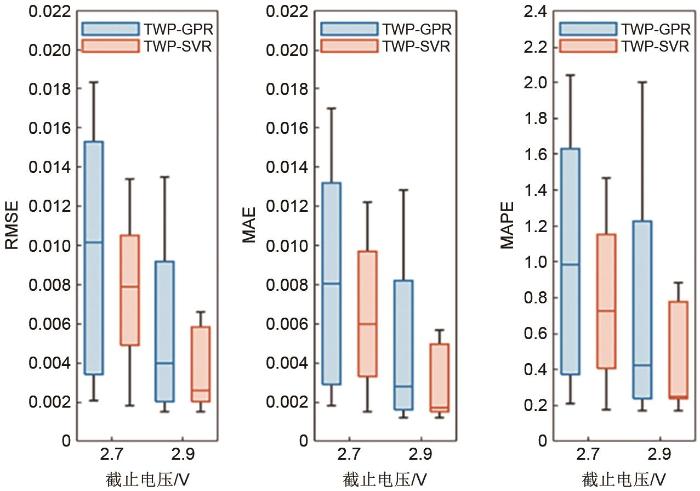
基于不同截止电压电池进行实验,两种模型评价指标分布如图15所示。由图15可知,对于不同截止电压,TWP-SVR模型的RMSE、MAE、MAPE指标分布范围均小于TWP-GPR模型。当截止电压为2.7 V时,TWP-SVR模型的RMSE、MAE、MAPE指标的中位数水平分别为0.008、0.006和0.7,均小于TWP-GPR模型的RMSE、MAE、MAPE指标的中位数水平0.01、0.08和0.99。当截止电压为2.9 V时,TWP-SVR模型的RMSE、MAE、MAPE指标的中位数水平分别为0.0024、0.0019和0.21,均小于TWP-GPR模型的RMSE、MAE、MAPE指标的中位数水平0.004、0.0023和0.4。这说明对于不同的截止电压,TWP-SVR模型的准确性优于TWP-GPR模型。
图 15
图 15
基于不同截至电压的两种模型SOH估计评价指标分布
Fig. 15
Evaluation index distribution of SOH estimation based on two models with different cut-off voltages
为评估两种拟合模型的稳定性,使用SSD和IQR对3个准确性指标做稳定性比较,21个电实验结果统计如表4所示。针对RMSE指标,TWP-SVR模型的SSD为0.0046,IQR为0.0061均低于TWP-GPR模型,表明以RMSE评价模型准确性,在21个电池实验中TWP-SVR模型的准确性指标波动不大,分布更集中,因此稳定性更高。同理,对于MAE指标,TWP-SVR模型的SSD为0.0044,IQR为0.0054均低于TWP-GPR模型,表明以MAE评价模型准确性,TWP-SVR模型稳定性优于TWP-GPR模型。对于MAPE指标,TWP-SVR模型的SSD为0.6886,略大于TWP-GPR模型,IQR为0.8410小于TWP-GPR模型。TWP_SVR模型的SSD大于TWP-GPR模型的情况可能是由于个别电池实验的指标异常引发的,IQR能更好地降低异常值的影响。因此IQR更能反映MAPE指标的稳定性。综合考虑对3个准确性指标进行SSD和IQR评估,可以说明,TWP-SVR模型在不同电池的准确性评估方面波动小,比TWP-GPR模型更加稳定。
表 4 基于TWP算法的SVR和GPR拟合模型的稳定性评价指标比较
Table 4
| 准确性指标 | 拟合模型 | 稳定性指标 | |
|---|---|---|---|
| 样本标准差SSD | 四分位差IQR | ||
| RMSE | TWP-SVR | 0.0046 | 0.0061 |
| TWP-GPR | 0.0051 | 0.0095 | |
| MAE | TWP-SVR | 0.0044 | 0.0054 |
| TWP-GPR | 0.0047 | 0.0092 | |
| MAPE | TWP-SVR | 0.6886 | 0.8410 |
| TWP-GPR | 0.5625 | 1.0553 | |
为验证两种拟合模型的准确性和稳定性,本工作是从不同截止电压方面比较了两种模型的绝对误差分布和评价指标。实验结果表明对于不同截止电压的NCA电池,在准确性和稳定性上,TWP-SVR模型均优于TWP-GPR模型。综合对比实验结果,本工作选择TWP-SVR模型。
2.4 基于实际运行数据的验证
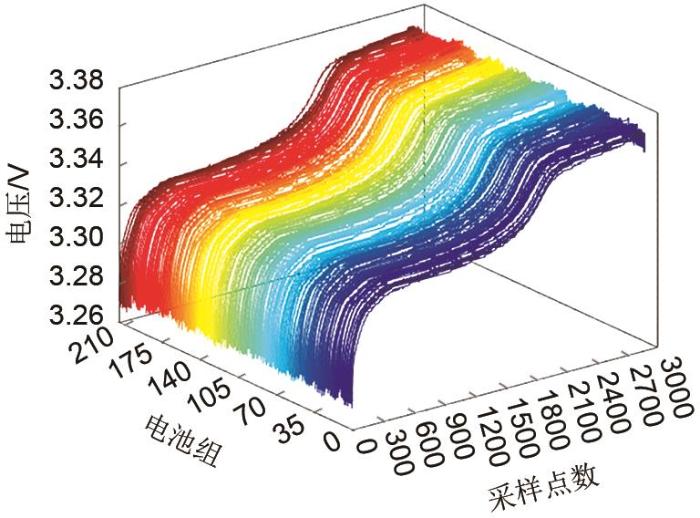
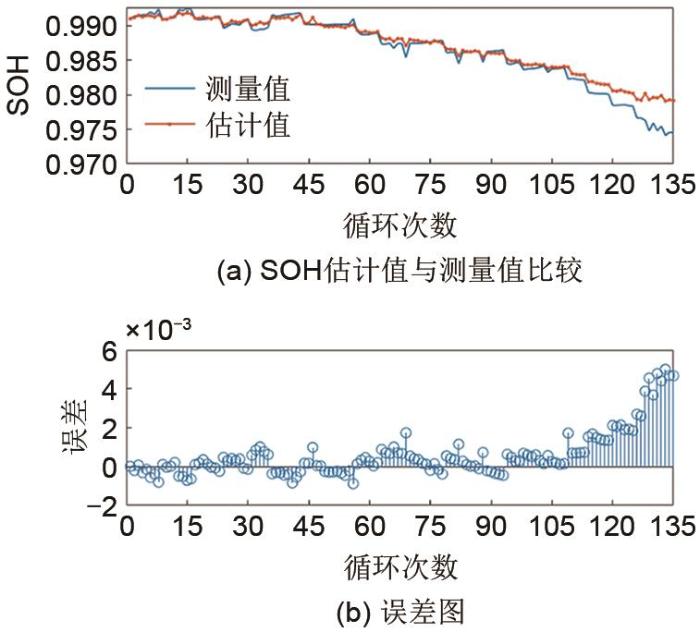
为验证所提方法在实际应用中的准确性,本工作使用储能电站实际运行的电池循环充放数据进行实验,数据采集信息见表5。实验数据包括216个LFP电池组的160次循环充放的电压和电流曲线。考虑电站充电阶段电流相对放电阶段更为平稳,本工作选择恒流充电阶段的电压曲线作为样本数据,由于采样周期小,数据量大,为了便于处理,只取前3000个数据。图16展示了储能电站在一个循环中充电阶段216个电池组的电压变化曲线;使用电站储能管理系统提供的SOH作为标签数据。实验取前15%(前24次的循环)充放数据作为训练数据,图17(a)展示了其中1个电池组的SOH估计值和测量值,图17(b)展示了SOH估计值和测量值之间的误差。使用TWP-SVR方法估计216个电池组的SOH,统计3种准确性指标,结果如图17所示。
表 5 储能电站数据采集详细信息
Table 5
| 参数 | 采样周期/ms | 误差/% | 计算周期/s | 更新周期/s | 备注 |
|---|---|---|---|---|---|
| 电流 | 25 | ±0.2 | 1 | 60 | 1秒钟计算一次平均电流,60秒后上传60个电流数据至服务器 |
| 电压 | 50 | ±0.3 | 1 | 60 | 1秒钟计算一次平均电压,60秒后上传60个电压数据至服务器 |
| 电荷量 | 25 | 2 | 1 | 60 | 根据电流采样值,使用安时积分法,1秒钟计算一次电荷量,60秒后计上传60个电荷量数据至服务器 |
| SOC | 25 | 2 | 1 | 60 | 根据电荷量计算荷电状态(SOC),每次放电初始值为100% |
| SOH | 25 | 2 | 1 | 60 | 根据电荷量计算SOH,电池组装机第一次放电时为100% |
图 16
图 16
储能电站充电阶段216个电池模组电压
Fig. 16
Voltage of 216 battery modules in charging stage of energy storage station
图 17
图 17
1个电池模组的SOH估计值与测量值比较及其误差分布
Fig. 17
Comparison of SOH estimated value and measured value of a battery module and its error distribution
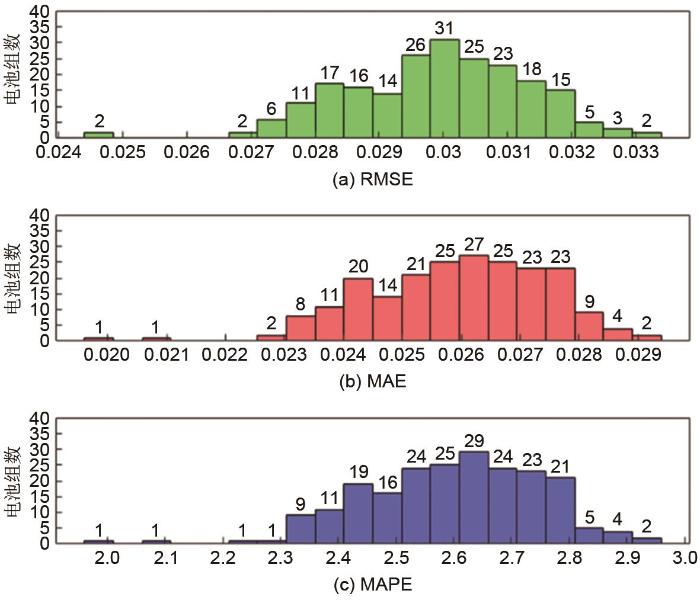
由图18可知,RMSE主要分布在0.003附近,MAE主要分布在0.0026附近,MAPE主要分布在0.26附近,3种指标数值较小,表明TWP-SVR方法具有较高的准确性。为评估TWP-SVR模型的稳定性,对216个电池组的3个准确性指标用SSD和IQR进行评估,统计结果如表6所示。由表6可知,RMSE、MAE和MAPE的SSD分别为0.0014、0.0015和0.0152;RMSE、MAE和MAPE的IQR分别为0.0020、0.0022和0.0220。可以看出对216个电池组使用TWP-SVR方法估计SOH值,模型的3个准确性指标的样本标准差和IQR均很小,说明TWP-SVR模型在不同电池中的准确性波动不大,模型具有较高的稳定性。
图 18
图 18
基于电站数据的TWP-SVR方法准确性评价指标
Fig. 18
Accuracy evaluation index of TWP-SVR method based on power station data
表 6 基于216个电池模组的TWP-SVR方法稳定性指标
Table 6
| 稳定性指标 | 准确性指标 | ||
|---|---|---|---|
| RMSE | MSE | MAPE | |
| 样本标准差SSD | 0.0014 | 0.0015 | 0.0152 |
| 四分位距IQR | 0.0020 | 0.0022 | 0.0220 |
3 结论
本工作从充放电电压曲线的相似性角度出发,提取间接健康特征估计LIBs的衰减容量和健康状态,所提出的TWP-SVR方法是利用TWP算法进行特征选择,SVR作为拟合模型的组合方法。其中TWP算法克服了计算非等长曲线相似性的困难,并且提取出了相关系数大于0.9的间接健康特征。在NASA数据集的实验中,TWP类型算法的RMSE小于0.031,MAE小于0.027,MAPE小于3.905,表明TWP算法具有较高的准确性。在UL-PUR开源数据集的实验中,SVR模型的RMSE、MAE和MAPE指标的IQR分别为0.0061、0.0054和0.8410,均小于GPR模型,表明SVR模型的稳定性更高。储能电站的真实运行数据验证实验结果为TWP-SVR模型的RMSE、MAE指标的样本标准差小于0.0015,四分位距小于0.0022,MAPE指标的样本标准差为0.0152,四分位距为0.0220,表明本工作所提出的TWP-SVR方法在保持较高准确性的同时具有良好的稳定性。
符号说明
| average Fréchet distance,平均弗雷歇距离 | |
| constant current,恒定电流 | |
| depth of discharge,放电深度 | |
| differential thermal voltammetry,差热伏安法 | |
| dynamic time warping,动态时间规整 | |
| differential voltage analysis,差分电压分析 | |
| gaussian process regression,高斯过程回归 | |
| gated recurrent unit,门控循环单元 | |
| incremental capacity analysis,增量容量分析 | |
| inter-quartile range,四分位距 | |
| lithium cobalt oxide (LiCoO2),钴酸锂 | |
| lithium iron phosphate (LiFePO4),磷酸铁锂 | |
| lithium-ion batteries,锂离子电池 | |
| long short term memory networks,长短期记忆网络 | |
| mean absolute error,平均绝对误差 | |
| mean absolute percentage error,平均绝对百分比误差 | |
| root mean square error,均方根误差 | |
| National Aeronautics and Space Administration,国家航空航天局(美国) | |
| lithium nickel cobalt aluminium oxide (LiNiCoAlO2),镍钴铝酸锂 | |
| lithium nickel manganese cobalt oxide (LiNiMnCoO2),镍钴锰酸锂 | |
| root mean square error,均方根误差 | |
| remaining useful life,剩余使用寿命 | |
| Sandia National Laboratories,桑迪亚国家实验室(美国) | |
| state of health,健康状态 | |
| sample standard deviation,样本标准差 | |
| support vector machine,支持向量机 | |
| support vector regression,支持向量回归 | |
| time warp profile,时间扭曲剖面图 | |
| Underwriters Laboratories Inc.-Purdue University,美国保险商实验室公司-普渡大学 |
参考文献